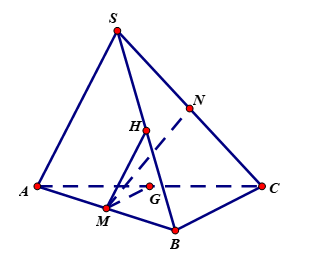
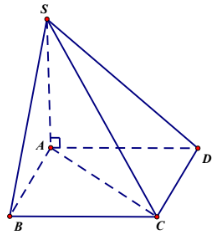
35 bài tập hai đường thẳng vuông góc mức độ nhận biết, thông hiểuLàm bàiCâu hỏi 1 : Cho hình chóp \(S.ABC\)có \(SA=BC=2a\) Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và\(SC\) và \(MN=a\sqrt{3}\). Tính số đo góc giữa hai đường thẳng \(SA\) và \(BC\)
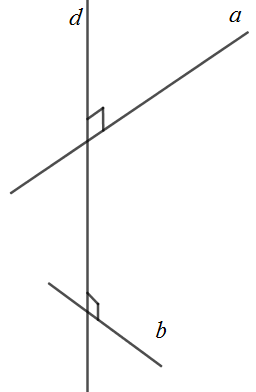
Đáp án: C Phương pháp giải: Xác định góc giữa hai đường thẳng d và d’: ta xác định đường thẳng d’’//d’ và d’’ cắt d. Khi đó góc giữa d và d’ là góc giữa d và d’’. Lời giải chi tiết:
Lấy H là trung điểm của SB, G là trung điểm của AC Ta có \(MH\text{//}SA\) và \(MG\text{//}BC\). Suy ra góc giữa hai đường thẳng \(SA\) và \(BC\)bằng góc giữa hai đường thẳng \(MH\) và \(MG\) . Ta có \(MH=NG=\frac{1}{2}SA=a;MG=HN=\frac{1}{2}BC=a;SA=BC(gt)\Rightarrow MH=MG=HN=NG=a\) Tứ giác \(MGNH\) là hình thoi cạnh \(a\) và \(MN=a\sqrt{3}\) suy ra \(HMG\) là tam giác đều. Vậy góc giữa hai đường thẳng \(SA\) và \(BC\) bằng \({{60}^{o}}\). Chọn C. Câu hỏi 2 : Mệnh đề nào sau đây sai ?
Đáp án: D Phương pháp giải: Dựa vào lí thuyết quan hệ vuông góc trong không gian. Lời giải chi tiết: Đáp án D. Vì hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng có thể cắt nhau, chéo nhau. Chọn D Câu hỏi 3 : Trong không gian cho đường thẳng \(\Delta \) và điểm O. Qua O có mấy đường thẳng vuông góc với \(\Delta \) ?
Đáp án: C Phương pháp giải: Dựa vào lý thuyết hình học phẳng đã được học để làm. Lời giải chi tiết: Qua đường một điểm nằm ngoài đường thẳng có thể kẻ được vô số đường vuông góc với đường thẳng đã cho. Chọn C Câu hỏi 4 : Cho tứ diện đều \(ABCD.\) Góc giữa hai đường thẳng \(AB\) và \(CD\) bằng
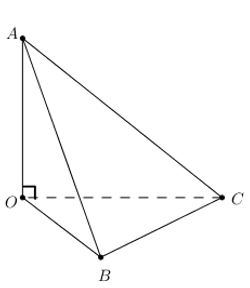
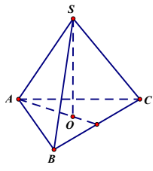
Đáp án: B Phương pháp giải: Tứ diện đều có cặp cạnh đối vuông góc với nhau Lời giải chi tiết: Gọi \(M\) là trung điểm của \(CD.\) Hai tam giác \(ACD,\,\,BCD\) đều \(\Rightarrow \,\,\left\{ \begin{align} & AM\bot CD \\ & BM\bot CD \\ \end{align} \right.\) \(\Rightarrow \,\,CD\bot \left( ABM \right)\Rightarrow \,\,CD\bot AB.\) Vậy góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({{90}^{0}}.\) Chọn B Câu hỏi 5 : Tứ diện OABC, OA, OB, OC đôi một vuông góc. Tính \(\widehat{\left( OA;BC \right)}\).
Đáp án: D Phương pháp giải: Lời giải chi tiết:
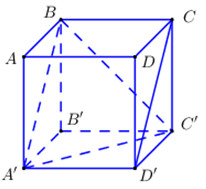
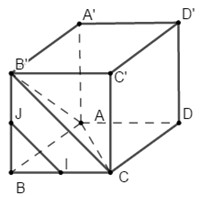
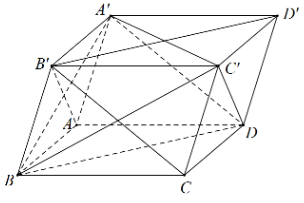
\(\left\{ \begin{align} OA\bot OB \\ OA\bot OC \\ \end{align} \right.\Rightarrow OA\bot \left( OBC \right)\Rightarrow OA\bot BC\Rightarrow \widehat{\left( OA;BC \right)}={{90}^{0}}\). Chọn đáp án D. Câu hỏi 6 : Cho hình lập phương \(ABCD.A'B'C'D'.\) Góc giữa hai đường thẳng \(A'C'\) và \(BD\) có số đo là bao nhiêu?
Đáp án: C Phương pháp giải: Ta có: \(\angle \left( {a;\,\,b} \right) = \angle \left( {a';\,\,b} \right)\) với \(a//a'.\) Lời giải chi tiết: Ta có: \(A'C'//AC \Rightarrow \angle \left( {A'C';\,\,BD} \right) = \angle \left( {AC;\,\,BD} \right)\) Mà \(ABCD\) là hình vuông \( \Rightarrow \angle \left( {AC,\,\,BD} \right) = {90^0}.\) Chọn C. Câu hỏi 7 : Trong không gian cho ba đường thẳng phân biệt \(a,\,\,b,\,\,c\). Khẳng định nào sau đây đúng?
Đáp án: B Phương pháp giải: Suy luận từng đáp án, có thể dùng hình vẽ để trực quan hơn. Lời giải chi tiết: A sai do nếu \(a\) và \(b\) cùng vuông góc với \(c\) thì hoặc \(a\parallel b\), hoặc \(a\) và \(b\) chéo nhau. C sai do: Giả sử hai đường thẳng \(a\) và \(b\) chéo nhau, ta dựng đường thẳng \(c\) cùng vuông góc với \(a\) và \(b\) và cắt cả hai đường thẳng \(a\) và \(b\). Khi đó \(\angle \left( {a;c} \right) = \angle \left( {b;c} \right) = {90^0}\) nhưng hiển nhiên \(a\) và \(b\) không vuông góc với nhau. D sai do: Giả sử \(a \bot c,\,\,b\parallel c\). Khi đó \(\angle \left( {a;c} \right) = {90^0}\), còn \(\angle \left( {b;c} \right) = {0^0}\). Chọn B. Câu hỏi 8 : Mệnh đề nào sau đây là đúng?
Đáp án: D Phương pháp giải: Sử dụng nhận xét và hai đường thẳng vuông góc. Lời giải chi tiết: Mệnh đề đúng là D: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia. Chọn D. Câu hỏi 9 : Cho hình hộp \(ABCD.A'B'C'D'\). Giả sử tam giác \(AB'C\) và \(A'DC'\) đều có 3 góc nhọn. Góc giữa hai đường thẳng \(AC\) và \(A'D\) là góc nào sau đây?
Đáp án: D Phương pháp giải: - Sử dụng định lí: \(a\parallel c \Rightarrow \angle \left( {a;b} \right) = \angle \left( {c;b} \right)\). - Góc giữa hai đường thẳng luôn nhỏ hơn hoặc bằng \({90^0}\). Lời giải chi tiết:
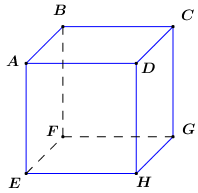
Ta có: \(AC\parallel A'C'\) (tính chất hình hộp) \( \Rightarrow \angle \left( {AC;A'D} \right) = \angle \left( {A'C';A'D} \right) = \angle DA'C'\) (do giả thiết cho tam giác \(DA'C'\) nhọn). Chọn D. Câu hỏi 10 : Cho hình lập phương \(ABCD.EFGH\). Hãy xác định góc giữa hai cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DH} \)?
Đáp án: B Phương pháp giải: Sử dụng định lí: Nếu \(a\parallel b\) và \(c \bot a\) và \(c \bot b\). Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}AB \bot AE\\AE\parallel DH\end{array} \right. \Rightarrow AB \bot DH\). Vậy \(\angle \left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = {90^0}\). Chọn B. Câu hỏi 11 : Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
Đáp án: C Phương pháp giải: Lời giải chi tiết: Phương pháp: Các mệnh đề “Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại” “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau." là các mệnh đề sai vì tồn tại 3 đường thẳng đôi một vuông góc Mệnh đề “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau” là sai vì tồn tại 2 đường thẳng song song cùng vuông góc với 1 đường thẳng thứ 3 Mệnh đề “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.” là đúng Chọn đáp án C Câu hỏi 12 : Phát biểu nào sau đây sai?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D: Là phát biểu sai, 2 đường thẳng này có thể chéo nhau. Chọn D. Câu hỏi 13 : Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:
Đáp án: C Phương pháp giải: +) Tứ diện đều có tất cả các cạnh đều bằng nhau. +) Sử dụng quy tắc: đường thẳng \(a\bot \left( P \right)\Rightarrow a\) vuông góc với mọi đường thẳng nằm trong (P). Lời giải chi tiết: Gọi M là trung điểm của \(CD\Rightarrow \left\{ \begin{align} & BM\bot CD \\ & AM\bot CD \\ \end{align} \right.\Rightarrow CD\bot \left( ABM \right)\Rightarrow CD\bot AB.\) \(\Rightarrow \widehat{\left( CD;\,\,AB \right)}={{90}^{0}}.\) Chọn C. Câu hỏi 14 : Trong không gian cho các đường thẳng \(a,b,c\) và mặt phẳng \(\left( P \right)\). Mệnh đề nào sau đây sai?
Đáp án: B Phương pháp giải: Suy luận từng đáp án. Lời giải chi tiết: Nếu \(a\bot b\) và \(b\bot c\) thì \(b\bot \left( a;c \right)\Rightarrow \) ta không thể kết luận a // c. Chọn B. Câu hỏi 15 : Cho hình lập phương \(ABCD.A'B'C'D'.\) Góc giữa hai đường thẳng \(BA'\) và \(CD\) bằng:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Câu hỏi 16 : Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng (P). Mệnh đề nào sau đây đúng?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Mệnh đề A đúng. Chọn A. Câu hỏi 17 : Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng \(a\). Góc giữa hai đường thẳng \(CD'\) và \(A'C'\) bằng
Đáp án: C Phương pháp giải: \(\angle \left( {a;b} \right) = \angle \left( {a;b'} \right)\,\,\left( {b'//b} \right)\) Lời giải chi tiết:
Ta có: \(CD'//A'B \Rightarrow \angle \left( {CD';A'C'} \right) = \angle \left( {A'B;A'C'} \right)\). Áp dụng định lí Pytago ta tính được \(A'B = A'C' = BC' = a\sqrt 2 \Rightarrow \Delta A'BC'\) đều \( \Rightarrow \angle \left( {A'B;A'C'} \right) = \angle BA'C' = {60^0}\). Vậy \(\angle \left( {CD';A'C'} \right) = {60^0}\). Chọn C. Câu hỏi 18 : Trong không gian cho đường thẳng \(\Delta \) và điểm \(O\). Qua \(O\) có bao nhiêu đường thẳng vuông góc với \(\Delta \)?
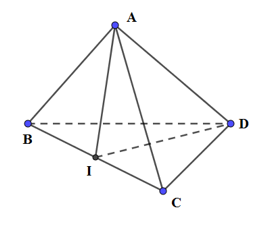
Đáp án: B Phương pháp giải: \(d \bot \left( P \right) \Rightarrow d \bot a\,\,\forall a \subset \left( P \right)\) Lời giải chi tiết: Trong không gian cho đường thẳng \(\Delta \) và điểm \(O\). Qua \(O\) có vô số đường thẳng vuông góc với \(\Delta \). Chúng nằm trong mặt phẳng qua \(O\) và vuông góc với \(\Delta \). Chọn B. Câu hỏi 19 : Cho tứ diện ABCD có \(AB = AC,\,\,BD = DC\). Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap c \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\) Lời giải chi tiết:
Gọi I là trung điểm của BC. Ta có: \(AB = AC,\,\,BD = DC \Rightarrow \Delta ABC,\,\,\Delta BCD\) là hai tam giác cân lần lượt tại đỉnh A và D. \( \Rightarrow \left\{ \begin{array}{l}AI \bot BC\\DI \bot BC\end{array} \right. \Rightarrow BC \bot \left( {AID} \right)\,\,\, \Rightarrow BC \bot AD\). Chọn: C Câu hỏi 20 : Góc giữa hai đường thẳng bất kỳ trong không gian là góc giữa:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Góc giữa hai đường thẳng bất kỳ trong không gian là góc giữa hai đường thẳng cùng đi qua một điểm và lần lượt song song với chúng. Chọn C. Câu hỏi 21 : Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc. Biết \(OA = OB = OC = a\), tính diện tích tam giác \(ABC\).
Đáp án: B Phương pháp giải: Công thức tính diện tích tam giác đều cạnh \(a:\,\,S = \frac{{{a^2}\sqrt 3 }}{4}\). Lời giải chi tiết: Dễ thấy \(\Delta OAB = \Delta OAC = \Delta OBC\,\,\left( {c.g.c} \right) \Rightarrow AB = AC = BC\). \( \Rightarrow \) Tam giác \(ABC\) đều cạnh \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) \({S_{ABC}} = \dfrac{{{{\left( {a\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\). Chọn B. Câu hỏi 22 : Cho hình lập phương \(ABCD.A'B'C'D'\) có \(I,\,\,J\) tương ứng là trung điểm của \(BC,\,\,BB'\). Góc giữa hai đường thẳng \(AC,\,\,IJ\) bằng:
Đáp án: C Phương pháp giải: \(a\parallel b \Rightarrow \angle \left( {a;c} \right) = \angle \left( {b;c} \right)\). Lời giải chi tiết:
Gọi độ dài hình lập phương là \(a\). Ta có \(I,\,\,J\) lần lượt là trung điểm của \(BC,\,\,BB'\) \( \Rightarrow IJ\) là đường trung bình của tam giác \(BB'C\)\( \Rightarrow IJ\parallel B'C\) Khi đó \(\angle \left( {AC;IJ} \right) = \angle \left( {AC;B'C} \right) = \angle ACB'\) Áp dụng định lí Pytago trong các tam giác vuông \(ABC,\) \(BB'C\), \(AA'B'\) ta tính được \(AC = AB' = B'C = a\sqrt 2 \). Suy ra tam giác \(AB'C\) là tam giác đều \( \Rightarrow \angle ACB' = {60^0}.\) Vậy \(\angle \left( {AC;IJ} \right) = {60^0}.\) Chọn C. Câu hỏi 23 : Cho tứ diện \(ABCD\) có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song song với một cặp cạnh đối diện của tứ diện. Trong các mệnh đề sau mệnh đề nào đúng?
Đáp án: A Phương pháp giải: Sử dụng các dấu hiệu nhận biết hình bình hành và hình chữ nhật. Lời giải chi tiết:
Giả sử cắt tứ diện đó bằng một mặt phẳng song song với \(BD,\,\,AC\). Giả sử thiết diện là \(MNPQ\). Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {ABD} \right) = MQ\\\left( {MNPQ} \right) \cap \left( {BCD} \right) = NP\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\end{array} \right. \Rightarrow MQ\parallel NP\parallel BD\). CMTT ta có \(MN\parallel PQ\parallel AC\). \( \Rightarrow MNPQ\) là hình bình hành. Lại có \(AC \bot BD\,\,\left( {gt} \right)\) nên \(MN \bot MQ\). Vậy tứ giác \(MNPQ\) là hình chữ nhật. Chọn A. Câu hỏi 24 : Cho hình chóp \(S.ABC\) có \(SA = SB = SC\) và \(\angle ASB = \angle BSC = \angle CSA\). Hãy xác định góc giữa hai vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \)?
Đáp án: D Phương pháp giải: - Sử dụng công thức trừ vectơ \(\overrightarrow {AB} = \overrightarrow {SB} - \overrightarrow {SA} \). - Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\). Lời giải chi tiết:
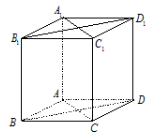
Ta có: \(\begin{array}{l}\overrightarrow {SC} .\overrightarrow {AB} = \overrightarrow {SC} \left( {\overrightarrow {SB} - \overrightarrow {SA} } \right) = \overrightarrow {SC} .\overrightarrow {SB} - \overrightarrow {SC} .\overrightarrow {SA} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = SC.SB.\cos \angle BSC - SC.SA.\cos \angle ASC\end{array}\) Vì \(SA = SB = SC\) và \(\angle ASB = \angle BSC = \angle CSA\) nên \(\overrightarrow {SC} .\overrightarrow {AB} = 0\). Vậy \(\left( {\overrightarrow {SC} ;\overrightarrow {AB} } \right) = {90^0}\). Chọn D. Câu hỏi 25 : Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Chọn khẳng định sai?
Đáp án: B Phương pháp giải: - Tính tích vô hướng giữa hai vectơ \(\overrightarrow {A{A_1}} ;\,\,\overrightarrow {{B_1}{D_1}} \). - Hình lập phương có các mặt đều là hình vuông. Lời giải chi tiết:
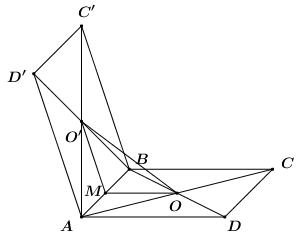
Ta có: \(\begin{array}{l}\overrightarrow {A{A_1}} .\overrightarrow {{B_1}{D_1}} = \overrightarrow {B{B_1}} .\overrightarrow {BD} = \overrightarrow {B{B_1}} \left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {B{B_1}} .\overrightarrow {BA} + \overrightarrow {B{B_1}} .\overrightarrow {BC} = 0\end{array}\) Vì \(\left( {\overrightarrow {B{B_1}} ;\overrightarrow {BA} } \right) = {90^0}\), \(\left( {\overrightarrow {B{B_1}} ;\overrightarrow {BC} } \right) = {90^0}\)). Do đó \(\left( {\overrightarrow {A{A_1}} ;\overrightarrow {{B_1}{D_1}} } \right) = {90^0}\) \( \Rightarrow \left( {A{A_1};{B_1}{D_1}} \right) = {90^0}\). Chọn B. Câu hỏi 26 : Cho hình hộp \(ABCD.A'B'C'D'\) có tất cả các cạnh bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?
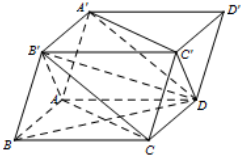
Đáp án: B Phương pháp giải: Sử dụng định lí: Nếu \(a\parallel b\) và \(c \bot a\) và \(c \bot b\). Lời giải chi tiết:
A đúng vì \(\left\{ \begin{array}{l}A'C' \bot B'D'\\B'D'\parallel BD\end{array} \right. \Rightarrow A'C' \bot BD\) . C đúng vì \(\left\{ \begin{array}{l}A'B \bot AB'\\AB'\parallel DC'\end{array} \right. \Rightarrow A'B' \bot DC'\). D đúng vì \(\left\{ \begin{array}{l}BC' \bot B'C\\B'C\parallel A'D\end{array} \right. \Rightarrow BC' \bot A'D\). Chọn B. Câu hỏi 27 : Cho \(\overrightarrow a = 3,\,\,\overrightarrow b = 5\) và góc giữa chúng bằng \({120^0}\). Chọn khẳng định sai trong các khẳng định sau:
Đáp án: D Phương pháp giải: Tính \({\left| {\overrightarrow a + \overrightarrow b } \right|^2}\), \({\left| {\overrightarrow a - \overrightarrow b } \right|^2}\), \({\left| {\overrightarrow a - 2\overrightarrow b } \right|^2}\), \({\left| {\overrightarrow a + 2\overrightarrow b } \right|^2}\). Lời giải chi tiết: Xét đáp án A: \(\begin{array}{l}{\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\overrightarrow a ^2} + {\overrightarrow b ^2} + 2\overrightarrow a \overrightarrow b \cos \left( {\overrightarrow a ;\overrightarrow b } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {3^2} + {5^2} + 2.3.5.cos{120^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 19\\ \Rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {19} \end{array}\) \(\Rightarrow\) Đáp án A đúng. Xét đáp án B: \(\begin{array}{l}{\left| {\overrightarrow a - \overrightarrow b } \right|^2} = {\overrightarrow a ^2} + {\overrightarrow b ^2} - 2\overrightarrow a \overrightarrow b \cos \left( {\overrightarrow a ;\overrightarrow b } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {3^2} + {5^2} - 2.3.5.cos{120^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 49\\ \Rightarrow \left| {\overrightarrow a - \overrightarrow b } \right| = \sqrt {7} \end{array}\) \(\Rightarrow\) Đáp án B đúng. Xét đáp án C: \(\begin{array}{l}{\left| {\overrightarrow a - 2\overrightarrow b } \right|^2} = {\overrightarrow a ^2} + 4{\overrightarrow b ^2} - 4\overrightarrow a \overrightarrow b \cos \left( {\overrightarrow a ;\overrightarrow b } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {3^2} + {5^2} - 4.3.5.cos{120^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 139\\ \Rightarrow \left| {\overrightarrow a - \overrightarrow b } \right| = \sqrt {139} \end{array}\) \(\Rightarrow\) Đáp án C đúng. Xét đáp án D: \(\begin{array}{l}{\left| {\overrightarrow a + 2\overrightarrow b } \right|^2} = {\overrightarrow a ^2} + 4{\overrightarrow b ^2} + 4\overrightarrow a \overrightarrow b \cos \left( {\overrightarrow a ;\overrightarrow b } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {3^2} + {5^2} + 4.3.5.cos{120^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 79\\ \Rightarrow \left| {\overrightarrow a - \overrightarrow b } \right| = \sqrt {79} \end{array}\) \(\Rightarrow\) Đáp án D sai. Chọn D. Câu hỏi 28 : Cho tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ABD\) là các tam giác đều. Khẳng định nào sau đây là đúng nhất.
Đáp án: B Phương pháp giải: - Sử dụng công thức trừ vectơ: \(\overrightarrow {CD} = \overrightarrow {AD} - \overrightarrow {AC} \). - Sử dụng công thức tính tích vô hướng \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\). Lời giải chi tiết: Đặt \(AB = AD = AC = a\). Ta có: \(\begin{array}{l}\overrightarrow {CD} .\overrightarrow {AB} = \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right).\overrightarrow {AB} \\ = AD.AB.\cos {60^0} - AC.AB.\cos {60^0}\\ = a.a.\dfrac{1}{2} - a.a.\dfrac{1}{2} = 0\end{array}\) Vậy \(AB \bot CD\). Chọn B. Câu hỏi 29 : Trong không gian cho hai hình vuông \(ABCD\) và \(ABC'D'\) có chung cạnh \(AB\) và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm \(O\) và \(O'\). Hãy xác định góc giữa hai cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {OO'} \)?
Đáp án: D Phương pháp giải: - Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(OM \bot AB\) và \(O'M \bot AB\). - Sử dụng công thức trừ vectơ: \(\overrightarrow {OO'} = \overrightarrow {MO'} - \overrightarrow {MO} \). - Tính \(\overrightarrow {OO'} .\overrightarrow {AB} \). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(AB\). Ta có \(OM\) là đường trung bình của tam giác \(ABC\) nên \(OM\parallel BC\). Mà \(BC \bot AB\) nên \(OM \bot AB\). CMTT ta có \(O'M \bot AB\). Ta có: \(\overrightarrow {OO'} .\overrightarrow {AB} = \left( {\overrightarrow {MO'} - \overrightarrow {MO} } \right).\overrightarrow {AB} \)\( = \overrightarrow {MO'} .\overrightarrow {AB} - \overrightarrow {MO} .\overrightarrow {AB} = 0\). Vậy \(OO' \bot AB\) hay \(\angle \left( {OO';AB} \right) = {90^0}\). Chọn D. Câu hỏi 30 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(\sqrt 3 a,\,\) \(SA\) vuông góc với mặt phẳng đáy và \(SA = \sqrt 2 a\) (minh họa như hình bên). Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
Đáp án: B Phương pháp giải: Góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(a\) và hình chiếu của nó trên mặt phẳng \(\left( P \right).\) Lời giải chi tiết: Ta có: \(SA \bot \left( {ABCD} \right)\)\( \Rightarrow AC\) là hình chiếu của \(SA\) trên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SC,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SC;\,\,AC} \right) = \angle SCA.\) Ta có \(ABCD\) là hình vuông cạnh \(\sqrt 3 a\) \( \Rightarrow AC = \sqrt 3 a.\sqrt 2 = a\sqrt 6 .\) Xét \(\Delta SAC\) vuông tại \(A\) ta có: \(\begin{array}{l}\tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 2 }}{{a\sqrt 6 }} = \dfrac{1}{{\sqrt 3 }}\\ \Rightarrow \angle SCA = {30^0}.\end{array}\) Chọn B. Câu hỏi 31 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng đáy và \(SA = 2a\). Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) là \(\alpha \). Khi đó \(\tan \alpha \) bằng:
Đáp án: A Phương pháp giải: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó. Lời giải chi tiết:
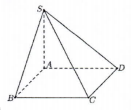
Vì \(SA \bot \left( {ABCD} \right)\) nên \(AC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA = \alpha \). Xét tam giác \(SAC\) vuông tại \(A\) có: \(AC = a\sqrt 2 \) (do \(ABCD\) là hình vuông cạnh \(a\)), \(SA = 2a\,\,\left( {gt} \right)\). \( \Rightarrow \tan \alpha = \dfrac{{SA}}{{AC}} = \dfrac{{2a}}{{a\sqrt 2 }} = \sqrt 2 .\) Chọn A. Câu hỏi 32 : Cho hình chóp tam giác đều \(S.ABC\) có độ dài cạnh đáy bằng \(a\). Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng \({60^0}\)?
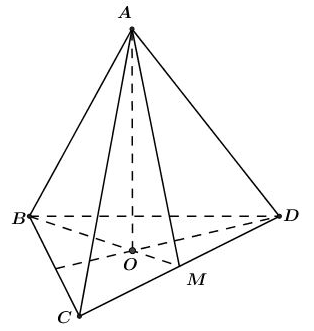
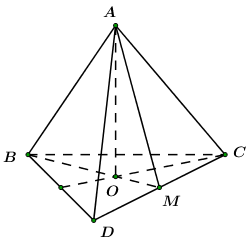
Đáp án: A Phương pháp giải: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó. Lời giải chi tiết:
Gọi \(O\) là tâm của tam giác đều \(ABC\) \( \Rightarrow SO \bot \left( {ABC} \right)\). \( \Rightarrow \) Hình chiếu của \(SA\) lên \(\left( {ABC} \right)\) là \(OA\). \( \Rightarrow \angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;OA} \right) = \angle SAO = {60^0}\). Xét tam giác vuông \(SAO\) có \(SA = \dfrac{{AO}}{{\cos {{60}^0}}} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}}}{{\dfrac{1}{2}}} = \dfrac{{2a}}{{\sqrt 3 }}\). Chọn A. Câu hỏi 33 : Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:
Đáp án: D Phương pháp giải: Gọi O là trọng tam tam giác BCD. Khi đó \(AO \bot \left( {BCD} \right).\) Gọi M là trung điểm của CD. Chứng minh \(CD \bot \left( {ABM} \right) \Rightarrow CD \bot AB\) \( \Rightarrow \angle \left( {CD,\,\,AB} \right) = {90^0}\) Lời giải chi tiết:
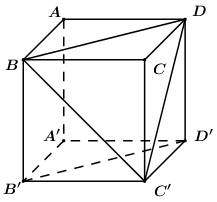
Gọi O là trọng tam tam giác BCD. Khi đó \(AO \bot \left( {BCD} \right).\) Gọi M là trung điểm của CD. Ta có: \(\left\{ \begin{array}{l}AM \bot CD\\AO \bot CD\end{array} \right. \Rightarrow CD \bot \left( {ABM} \right)\) \( \Rightarrow CD \bot AB\) \( \Rightarrow \angle \left( {CD,\,\,AB} \right) = {90^0}\) Chọn D. Câu hỏi 34 : Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(BC'\) và \(B'D'\) là:
Đáp án: C Phương pháp giải: Sử dụng định lí: \(a//b \Rightarrow \angle \left( {a;c} \right) = \angle \left( {b;c} \right)\) Lời giải chi tiết:
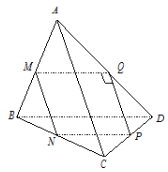
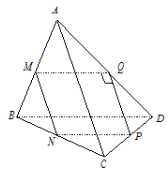
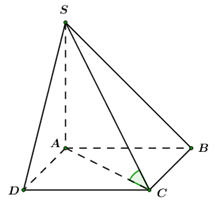
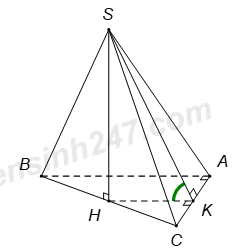
Do \(BD\parallel B'D'\) nên \(\angle \left( {BC';B'D'} \right) = \angle \left( {BC';BD} \right)\). Giả sử cạnh của hình lập phương bằng 1. Áp dụng định lí Pytago trong các tam giác vuông ta có: \(BC' = BD = C'D = \sqrt 2 \). Suy ra tam giác \(BC'D\) đều \( \Rightarrow \angle C'BD = {60^0}\). Vậy \(\angle \left( {BC';B'D'} \right) = {60^0}\). Chọn C. Câu hỏi 35 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại A, \(\widehat{ABC}={{60}^{\circ }}\), tam giác \(SBC\) là tam giác đều có bằng cạnh \(2a\) và nằm trong mặt phẳng vuông với đáy. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( SAC \right)\) và \(\left( ABC \right)\). Mệnh đề nào sau đây đúng?
Đáp án: B Phương pháp giải: Áp dụng phương pháp xác định góc giữa hai mặt phẳng Lời giải chi tiết:
Gọi \(H\) là trung điểm của \(BC\), suy ra \(SH\bot BC\Rightarrow SH\bot \left( ABC \right)\) Gọi \(K\) là trung điểm \(AC\), suy ra \(HK\parallel AB\) nên \(HK\bot AC\). Ta có \(\left\{ \begin{array}{l}AC \bot HK\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot SK.\) Do đó \(\widehat{\left( \left( SAC \right);\left( ABC \right) \right)}=\widehat{\left( SK,HK \right)}=\widehat{SKH}.\) Tam giác vuông \(ABC\), có \(AB=BC.\cos \widehat{ABC}=a\Rightarrow HK=\frac{1}{2}AB=\frac{a}{2}.\) Tam giác SBC đều cạnh 2a \(\Rightarrow SH=\frac{2a\sqrt{3}}{2}=a\sqrt{3}\) Tam giác vuông \(SHK\), có \(\tan \widehat{SKH}=\frac{SH}{HK}=2\sqrt{3}\). Chọn B. |