30 bài tập vận dụng về Bội chung nhỏ nhấtLàm bàiCâu hỏi 1 : Cô giáo Hồng có \(1\) số phần thưởng nhất định để tặng các bạn học sinh giỏi. Biết rằng nếu lớp có \(5\) bạn học sinh giỏi thì số vở các bạn nhận được là bằng nhau, nhưng nếu lớp có \(7\) bạn học sinh giỏi thì số vở các bạn vẫn nhận được là bằng nhau. Cô giáo Hồng cần ít nhất là bao nhiêu quyển vở để phát phần thưởng cho các bạn học sinh là:
Đáp án: C Phương pháp giải: - Vì số vở cô giáo chia cho \(5\) bạn, mỗi bạn đều có số vở như nhau nên số vở chia hết cho \(5\). Tương tự số vở chia cho \(7\) bạn, mỗi bạn có số vở bằng nhau, nên số vở chia hết cho \(7\). - Từ đó áp dụng kiến thức về bội chung của \(2\) số là \(5\) và \(7\) - Theo đề bài ra, số vở của cô giáo là ít nhất, nên đó là \(BCNN\left( 5,7 \right)\) Lời giải chi tiết:
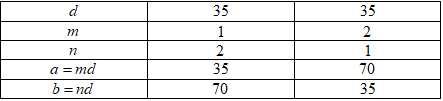
Hướng dẫn giải chi tiết: Gọi số vở ban đầu cô giáo Hồng có là: \(a\) (\(a>0,a\in N\)) Theo bài ra ta có: \(a\vdots 5;a\vdots 7\) Suy ra: \(a\in BC(5,7)\). Mà \(a\) là số nhỏ nhất nên: \(a=BCNN(5,7)\) Ta có \(5\) và \(7\) là \(2\) số nguyên tố nên \(BCNN(5,7)=5.7=35\) Vậy ban đầu cô giáo Hồng có số quyển vở là \(35\) (quyển) Chọn C Câu hỏi 2 : Hãy tính nhẩm \(BCNN\) của các số sau bằng cách nhân số lớn nhất với lần lượt các số \(1,2,3,\ldots \) cho đến khi kết quả là số chia hết cho các số còn lại. \(\begin{align}& \text{a)}40,160 \\& \text{b)}18,30,90 \\\end{align}\)
Đáp án: A Phương pháp giải: - Tính nhẩm \(BCNN\) của các số bằng cách: Lấy số lớn nhất nhân với \(n=1,2,3\ldots \) khi nào tìm được \(n\) để số đó chia hết cho các số ban đầu thì đó là \(BCNN\). Lời giải chi tiết: \({\rm{a)}}\,\,40,160\) Xét thấy \(160:40 = 4\) hay \(160 \vdots 40\), nên \(BCNN(160;40) = 160\) khi đó \(n = 1.\) \({\rm{b)}}\,\,18,30,90\) Ta có: \(90:\,\,18 = 5;\,\,90:30 = 3;\,\,90:90 = 1\) Vậy \(BCNN\left( {18,\,\,30,\,\,90} \right) = 90.\) Câu hỏi 3 : Trong đợt phát động phong trào “Tủ sách lớp học”, nhà trường đã thu về một số sách khi xếp thành từng bó 12 cuốn, 15 cuốn, 18 cuốn đều vừa đủ bó. Biết số sách trong khoảng từ 200 đến 500. Tính số sách nhà trường đã thu được.
Đáp án: D Phương pháp giải: Gọi x là số sách nhà trường đã thu được . Từ đề bài ta có \(x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,15\,\,;\,\,x\,\, \vdots \,\,18\) suy ra \(x \in BC\,(12;\,\,15;\,\,18)\) Tìm \(BCNN{\rm{ }}(12;15;{\rm{ }}18)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC(12;\;15;18).\) Kết hợp với điều kiện \(200\; < \;x\; < 500\) để tìm x. Lời giải chi tiết: Gọi x là số sách nhà trường đã thu được \(\left( {200 < x < 500} \right).\) Vì khi xếp thành từng bó 12 cuốn, 15 cuốn, 18 cuốn đều vừa đủ bó nên \(x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,15\,\,;\,\,x\,\, \vdots \,\,18\), suy ra \(x \in BC\,(12;\,\,15;\,\,18)\) Ta có: \(12\, = {2^2}.3\,\,\,;\,\,\,\,\,\,\,\,\,\,15 = 3.5\,\,;\,\,\,\,\,\,\,\,\,18 = {2.3^2}\). \(\begin{array}{l}BCNN(12\,;\,\,15\,;\,\,18) = {2^2}{.3^2}.5 = 180\\ \Rightarrow BC{\rm{ }}(12;{\rm{ }}15;{\rm{ }}18) = B\left( {180} \right) = \left\{ {0;{\rm{ 18}}0;{\rm{ 36}}0;{\rm{ 54}}0;{\rm{ }} \ldots } \right\}\end{array}\) Do đó: \(x \in \left\{ {0;{\rm{ 18}}0;{\rm{ 36}}0;{\rm{ 54}}0;{\rm{ }} \ldots } \right\}\) Lại có \(200 < x < 500\) nên \(x = 360\) . Vậy trường đó đã thu được 360 cuốn sách. Chọn D Câu hỏi 4 : Số học sinh khối THCS của trường THPT Chuyên Hà Nội – Amsterdam tham gia thi độ nghi thức trong khoảng từ \(800\) đến \(1000\) em, được xếp thành các hàng. Nếu xếp mỗi hàng \(20\) thì dư \(9\) em; nếu xếp mỗi hàng \(30\) thì thiếu \(21\)em; nếu xếp mỗi hàng \(35\) thì thiếu \(26\) em. Hỏi có tất cả bao nhiêu em dự thi nghi thức đội?
Đáp án: B Phương pháp giải: Gọi \(x\) là số học sinh dự thi nghi thức đội \(\left( {x \in {N^*},\;x > 9} \right).\) Từ đề bài ta có \((x - 9)\,\, \vdots \,\,20\,\,;\,\,(x - 9)\,\, \vdots \,\,30\,\,;\,\,(x - 9)\,\, \vdots \,\,35\) suy ra \(x - 9 \in BC\,(20;\,\,30;\,\,35)\) Tìm \(BC\,(20;\,\,30;\,\,35)\) bằng cách phân tích các số ra thừa số nguyên tố. Kết hợp với điều kiện \(800 < x < 1000\) để tìm x. Lời giải chi tiết: Gọi \(x\) là số học sinh dự thi nghi thức đội \((800 < x < 1000)\). Nếu xếp mỗi hàng \(20\) thì dư \(9\) em nên ta có \((x - 9)\,\, \vdots \,\,20\). Nếu xếp mỗi hàng \(30\) thì thiếu \(21\)em, tức là nếu xếp mỗi hàng \(30\) thì sẽ dư 9 em, do đó \((x - 9)\,\, \vdots \,\,30\). Nếu xếp mỗi hàng \(35\) thì thiếu \(26\)em, tức là nếu xếp mỗi hàng \(35\) thì sẽ dư 9 em, do đó \((x - 9)\,\, \vdots \,\,35\). Vậy \((x - 9)\,\, \vdots \,\,20\,\,;\,\,(x - 9)\,\, \vdots \,\,30\,\,;\,\,(x - 9)\,\, \vdots \,\,35\) suy ra \(x - 9 \in BC\,(20;\,\,30;\,\,35)\) Ta có: \(20\, = {2^2}.5\,\,\,;\,\,\,\,\,\,\,\,\,\,30 = 2.3.5\,\,;\,\,\,\,\,\,\,\,\,35 = 5.7\). \(BCNN(20\,;\,\,30\,;\,\,35) = {2^2}.3.5.7 = 420\). \(BC{\rm{ }}(20;{\rm{ 30}};{\rm{ 35}}) = B\left( {420} \right) = \left\{ {0;{\rm{ 420}};{\rm{ 840}};{\rm{ 126}}0;{\rm{ }} \ldots } \right\}\) Do đó: \(x - 9 \in \left\{ {0;{\rm{ 42}}0;{\rm{ 84}}0;{\rm{ 126}}0;{\rm{ }} \ldots } \right\}\) Suy ra \(x \in \left\{ {9;{\rm{ 429}};{\rm{ 849}};{\rm{ 1269}};{\rm{ }} \ldots } \right\}\) Lại có \(800 < x < 1000\) nên \(x = 849\) . Vậy có tất cả \(849\) em dự thi nghi thức đội. Chọn B. Câu hỏi 5 : Học sinh khối \(6\) của một trường khi xếp hàng \(6\), hàng \(8\), hàng \(12\) thì vừa đủ. Tính số học sinh khối \(6\) của trường đó, biết rằng số học sinh đó trong khoảng từ \(50\) đến \(80\) em.
Đáp án: B Phương pháp giải: Gọi \(x\) là số học sinh của khối \(6\) (\(50 \le x \le 80\) ). Từ đề bài ta có \(x\,\, \vdots \,\,6\,\,;\,\,x\,\, \vdots \,\,8\,\,;\,\,x\,\, \vdots \,\,12\) suy ra \(x \in BC\,(6;\,\,8;\,\,12)\) Tìm \(BCNN\left( {6;\,\,8;\,\,12} \right)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC\left( {6;\,\,8;\,\,12} \right)\). Kết hợp với điều kiện \(50 \le x \le 80\) để tìm \(x\).
Lời giải chi tiết: Gọi \(x\) là số học sinh của khối \(6\), \(x\) là số tự nhiên và \(50 \le x \le 80\) ). Vì học sinh lớp \(6A\) khi xếp hàng \(6\), hàng \(8\), hàng \(12\) đều vừa đủ hàng nên ta có \(x\,\, \vdots \,\,6\,\,;\,\,x\,\, \vdots \,\,8\,\,;\,\,x\,\, \vdots \,\,12\). Suy ra \(x \in BC\,(6;\,\,8;\,\,12)\) . Ta có: \(6 = 2.3\,;\,\,\,\,\,\,\,\,\,\,8 = {2^3}\,\,;\,\,\,\,\,\,\,\,\,12 = {2^2}.3\). \(\begin{array}{l} \Rightarrow BCNN(6;\,\,8;\,\,12) = {2^3}.3 = 24\\ \Rightarrow BC{\rm{ }}(6;\,\,8;\,\,12) = B\left( {24} \right) = \left\{ {0;{\rm{ 24}};{\rm{ 48}};{\rm{ 72}};{\rm{ }} \ldots } \right\}\end{array}\). Do đó: \(x \in \left\{ {0;{\rm{ 24}};{\rm{ 48}};{\rm{ 72}};{\rm{ }} \ldots } \right\}\) Lại có \(50 \le x \le 80\) nên \(x = 72\) (thỏa mãn điều kiện). Vậy khối lớp \(6\) có \(72\) học sinh. Chọn đáp án B Câu hỏi 6 : Một trường THCS cho tất cả các em học sinh xếp hàng dưới sân trường để tập diễu hành. Nếu xếp mỗi hàng 40, 45, 60 học sinh thì đều thừa 9 học sinh. Nhưng nếu xếp mỗi hàng 27 học sinh thì vừa đủ. Hỏi trường THCS đó có bao nhiêu học sinh. Biết rằng trường THCS đó có không quá 1000 học sinh?
Đáp án: B Phương pháp giải: Đọc kĩ đề bài, đặt ẩn thích hợp. Từ đó lập luận và giải toán tìm được kết quả đúng.
Lời giải chi tiết: Gọi số học sinh của trường đó là \(x\,\left( {x \in {N^*},\,x < 1000} \right)\) Vì xếp mỗi hàng 40, 45, 60 học sinh thì đều thừa 9 học sinh nên ta có: \(\left\{ \begin{array}{l}x - 9 \vdots 40\\x - 9 \vdots 45\\x - 9 \vdots 60\end{array} \right. \Rightarrow x - 9 \in BC\left( {40,45,60} \right)\) Mà: \(40 = {2^3}.5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,45 = {3^2}.5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,60 = {2^2}.3.5\,\,\,\,\,\,\, \Rightarrow BCNN\left( {40.45,60} \right) = {2^3}{.3^2}.5 = 8.9.5 = 360\) \(\begin{array}{l} \Rightarrow x - 9 \in \left\{ {360,720,1080,...} \right\}\\ \Rightarrow x \in \left\{ {369,\,729,\,1089,...} \right\}\end{array}\) Vì \(x < 1000\) nên \(x \in \left\{ {369;\,729} \right\}\) Nếu mỗi hàng 27 học sinh thì vừa đủ \( \Rightarrow x \vdots 27\) nên \(x = 729\) Vậy trường đó có 729 học sinh. Chọn B Câu hỏi 7 : Một trường tổ chức cho khoảng từ 400 đến 500 học sinh đi tham quan bằng ô tô. Tính số học sinh của trường đi tham quan, biết rằng nếu xếp 25 em hay 30 em vào một xe thì vừa đủ không thừa ai.
Đáp án: C Phương pháp giải: Giải toán đố về bội chung và ước chung. Đặt ẩn phù hợp, ở đây ta thấy nếu xếp 25 em hay 30 em vào một xe thì vừa đủ không thừa ai, do đó số học sinh đi tham quan phải là bội chung của 25, và 30, từ giả thiết bài toán ta đi tìm kết quả. Lưu ý : Đặt điều kiện cho ẩn.
Lời giải chi tiết: Gọi số học sinh đi tham quan của trường là x với \(x \in {N^*}\,\left( {400 \le x \le 500} \right)\) Vì nếu xếp 25 em hay 30 em vào một xe thì vừa đủ không thừa ai nên \(x \vdots 25\,\,;\,\,\,x \vdots 30 \Rightarrow x \in BC\left( {25,30} \right)\), Ta có : \(\begin{array}{l}25 = {5^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,30 = 2.3.5\\ \Rightarrow BCNN\left( {25;30} \right) = {2.3.5^2} = 150\end{array}\) \( \Rightarrow BC\left( {25;30} \right) = B\left( {150} \right) = \left\{ {0,150,300,450,600,...} \right\}\) Mà \(x \in {N^*}\left( {400 \le x \le 500} \right)\) nên \(x = 450\) Vậy số học sinh của trường là 450 học sinh. Chọn C Câu hỏi 8 : Số học sinh của một trường khi xếp thành 12 hàng, 15 hàng, 18 hàng đều vừa đủ. Hỏi trường đó có bao nhiêu học sinh? Biết số học sinh trong khoảng từ 500 đến 600 em.
Đáp án: C Phương pháp giải: Giải toán đố về bội chung và ước chung. Đặt ẩn phù hợp, ở đây ta thấy Số học sinh của trường khi xếp thành 12 hàng, 15 hàng, 18 hàng đều vừa đủ nên số học sinh sẽ thuộc tập hợp BC(12,15,18). Từ giả thiết bài toán ta đi tìm kết quả. Lưu ý : Đặt điều kiện cho ẩn.
Lời giải chi tiết: Gọi số học sinh của trường là \(x \in {N^*}\left( {500 \le x \le 600} \right)\) Số học sinh của trường khi xếp thành 12 hàng, 15 hàng, 18 hàng đều vừa đủ nên ta có: \(x \vdots 12,\,\,\,x \vdots 15,\,\,\,x \vdots 18\,\,\, \Rightarrow x \in BC\left( {12,15,18} \right)\) Ta có: \(\begin{array}{l}12 = {2^2}.3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,15 = 3.5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,18 = {2.3^2}\\ \Rightarrow BCNN\left( {12,15,18} \right) = {2^2}{.3^2}.5 = 180\\ \Rightarrow BC\left( {12,15,18} \right) = B\left( {180} \right) = \left\{ {0,180,360,540,720,...} \right\}\end{array}\) Mà \(x \in {N^*}\left( {500 \le x \le 600} \right)\)nên \(x = 540\) Vậy số học sinh của trường là 540 học sinh. Chọn C Câu hỏi 9 : Tìm hai số tự nhiên \(a\) và \(b\), biết \(BCNN\left( {a,b} \right) = 90\) và \(a.b = 900\).
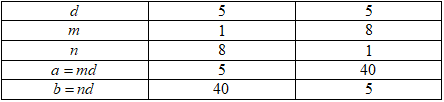
Đáp án: D Phương pháp giải: Dạng bài: Tìm hai số tự nhiên \(a\) và \(b\)khi biết tích và bội chung nhỏ nhất. +) Áp dụng công thức \(BCNN\left( {a;b} \right) = k \Rightarrow \left\{ \begin{array}{l}k = am\\k = bn\end{array} \right. \left( {m;n} \right) = 1,\,\,\left( {m,\,\,n \in {\mathbb{N}^*}} \right)\) +) Từ đó suy ra \(\left\{ \begin{array}{l}a = \frac{k}{m}\\b = \frac{k}{n}\end{array} \right.\) thay vào tích \(a.b\) \( \Rightarrow \)Giá trị của \(m\) và \(n\)\( \Rightarrow \) Tìm được \(a\) và \(b\). Lời giải chi tiết: Theo bài ra ta có: \(BCNN\left( {a,b} \right) = 90 \Rightarrow \left\{ \begin{array}{l}90 = a.m\\90 = b.n\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{{90}}{m}\\b = \frac{{90}}{n}\end{array} \right. \left( {m,n} \right) = 1,\,\,\,\left( {m,\,\,n \in {\mathbb{N}^*}} \right)\) Mà \(a.b = 900 \Rightarrow \frac{{90}}{m} \cdot \frac{{90}}{n} = 900 \Rightarrow \frac{{8100}}{{m.n}} = 900 \Rightarrow m.n = 9\). Vì \(\left( {m,n} \right) = 1\) nên ta có: +) Với \(m = 1,n = 9 \Rightarrow a = 90,b = 10\). +) \(m = 9,n = 1 \Rightarrow a = 10,b = 90\). Vậy cặp số \(\left( {a;b} \right)\) cần tìm là \(\left( {90;10} \right),\left( {10;90} \right)\). Chọn D. Câu hỏi 10 : Tìm hai số tự nhiên \(a\) và \(b\), biết \(UCLN\left( {a,b} \right) = 6\) và \(BCNN\left( {a,b} \right) = 180\).
Đáp án: C Phương pháp giải: Dạng bài: Tìm hai số tự nhiên khi biết ước chung lớn nhất và bội chung nhỏ nhất của hai số đó +) Xác định \(a.b\) bằng cách áp dụng công thức \(UCLN\left( {a,b} \right).BCNN\left( {a,b} \right) = ab\) Lời giải chi tiết: Theo đề bài ta có: \(\left\{ \begin{array}{l}UCLN\left( {a,b} \right) = 6\\BCNN\left( {a,b} \right) = 180\end{array} \right. \Rightarrow a.b = 1080\) \(\left( 1 \right)\) Từ \(UCLN\left( {a,b} \right) = 6 \Rightarrow \left\{ \begin{array}{l}a = 6.m\\b = 6.n\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,{\left( 2 \right)^{\begin{array}{*{20}{c}}{}&{}\end{array}}}\left( {m,n} \right) = 1\) Thay \(\left( 2 \right)\) vào \(\left( 1 \right)\) ta được: \(6.m.6.n = 1080 \Rightarrow m.n = 30\) Mà \(\left( {m,n} \right) = 1\) nên ta có bảng sau: Suy ra Vậy các cặp số \(\left( {a;b} \right)\) cần tìm là \(\left( {6;180} \right),\left( {180;6} \right),\left( {12;90} \right),\left( {90;12} \right),\left( {30;36} \right),\left( {36;30} \right),\left( {18;60} \right),\left( {60;18} \right)\). Chọn C. Câu hỏi 11 : Tìm hai số tự nhiên \(a\)và \(b\), biết \(\frac{a}{b} = \frac{4}{5}\) và \(BCNN\left( {a;b} \right) = 140\).
Đáp án: A Phương pháp giải: Dạng bài: Tìm hai số tự nhiên khi biết tỉ số và bội chung nhỏ nhất của hai số đó +) Đặt \(\left( {a;b} \right) = k\) với \(k \in {\mathbb{N}^*}\). \( \Rightarrow a\) và \(b\) được biểu diễn theo \(k\) +) Xác định tích \(ab\) thông qua công thức \(ab = UCLN\left( {a,b} \right).BCNN\left( {a,b} \right)\) Lời giải chi tiết: Đặt \(UCLN\left( {a,b} \right) = k \left( {k \in {\mathbb{N}^*}} \right)\) +) \(\frac{a}{b} = \frac{4}{5} \Rightarrow \left\{ \begin{array}{l}a = 4k\\b = 5k\end{array} \right.\) +) \(ab = UCLN\left( {a,b} \right).BCNN\left( {a,b} \right)\) và \(BCNN\left( {a;b} \right) = 140\) \( \Rightarrow ab = k.140\) \(\begin{array}{l} \Rightarrow 4k.5k = k.140\\ \Rightarrow 20k = 140\\ \Rightarrow k = 7\end{array}\) Do đó, \(a = 28;b = 35\). Vậy \(\left( {a;b} \right) = \left( {28;35} \right).\) Chọn A. Câu hỏi 12 : Tìm hai số tự nhiên \(a\)và \(b\), biết \(a - b = 7\) và \(BCNN\left( {a;b} \right) = 140\).
Đáp án: B Phương pháp giải: Dạng bài: Tìm hai số tự nhiên \(a\) và \(b\) khi biết hiệu \((\)\(a - b = c\)\()\)và bội chung nhỏ nhất +) Đặt \(\left( {a,b} \right) = k{}^{}\left( {k \in {\mathbb{N}^*}} \right)\)\( \Rightarrow \left\{ \begin{array}{l}a = km\\b = kn\end{array} \right.\) +) Thay vào \(a - b = c\)\( \Rightarrow k \in U\left( c \right)\) +) Áp dụng \(BCNN\left( {a,b} \right).UCLN\left( {a,b} \right) = ab\) suy ra \(k \in U\left( {BCNN\left( {a,b} \right)} \right)\). \( \Rightarrow \) Xác định được \(k\)\( \Rightarrow m,n\) \( \Rightarrow \)Tìm được hai số \(a\) và \(b\). Lời giải chi tiết: Đặt \(\left( {a,b} \right) = k{}_{}\left( {k \in \mathbb{N}} \right)\) và \(a > b\). \( \Rightarrow \left\{ \begin{array}{l}a = km\\b = kn\end{array} \right. \left( {m,n} \right) = 1{,^{}}m > n\) Theo bài ra ta có: \(a - b = 7 \Leftrightarrow km - kn = 7 \Leftrightarrow k.\left( {m - n} \right) = 7 \Rightarrow k \in U\left( 7 \right)\) \(\left( 1 \right)\) Ta lại có: \(UCLN\left( {a,b} \right).BCNN\left( {a,b} \right) = ab\) \( \Rightarrow BCNN\left( {a,b} \right) = \frac{{ab}}{{UCLN\left( {a,b} \right)}} = \frac{{km.kn}}{k} = kmn \Rightarrow kmn = 140 \Rightarrow k \in U\left( {140} \right) \left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(k \in UC\left( {7,140} \right) \Rightarrow k \in \left\{ {1;7} \right\}\) +) Với \(k = 1 \Rightarrow m - n = 7\) và \(m.n = 140\)\( \Rightarrow \)không có giá trị của \(m\) và \(n\) thỏa mãn. +) Với \(k = 7 \Rightarrow m - n = 1\) và \(m.n = 20\) \( \Rightarrow m = 5;n = 4\) \( \Rightarrow \left\{ \begin{array}{l}a = k.m = 7.5 = 35\\b = k.n = 7.4 = 28\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 35\\b = 28\end{array} \right.\) Vậy cặp số \(\left( {a;b} \right)\) cần tìm là \(\left( {35;28} \right)\). Chọn B. Câu hỏi 13 : Hôm nay, ba bạn Nguyễn mang cả hai xe của ba và mẹ bạn ra tiệm để thay nhớt máy. Xe của ba bạn thì đúng \(30\) ngày thay nhớt một lần, còn xe của mẹ bạn thì đúng \(40\) ngày thay nhớt một lần. Em hãy cho biết thời gian nào gần nhất thì ba bạn Nguyễn lại đem cả \(2\)xe (của ba và mẹ) thay nhớt cùng một lúc.
Đáp án: D Phương pháp giải: Gọi \(x\) là số ngày ít nhất để ba bạn Nguyễn cùng đem cả \(2\) xe đi thay nhớt \(\left( {x \in {\mathbb{N}^*}} \right)\). Theo đề bài ta có \(x = BCNN\left( {30\,;\,\,40} \right)\) Tìm \(BCNN\left( {30\,;\,\,40} \right)\) bằng cách phân tích các số ra thừa số nguyên tố. Lời giải chi tiết: Gọi \(x\) là số ngày phải tìm \(\left( {x > 0} \right).\) Vì xe của ba bạn thì đúng \(30\) ngày thay nhớt một lần, còn xe của mẹ bạn thì đúng \(40\) ngày thay nhớt một lần và \(x\) là thời gian gần nhất để ba bạn Nguyễn cùng đem cả \(2\) xe đi thay nhớt nên suy ra \(x = BCNN\left( {30\,;\,\,40} \right)\). Ta có: \(30 = 2.3.5\,\,\,; 40 = {2^3}.5\) \( \Rightarrow BCNN\left( {30 \,;\,\,40} \right) = {2^3}.3.5 = 120\) Do đó \(x = 120\). Vậy ít nhất sau \(120\) ngày, ba bạn Nguyễn cùng đem cả \(2\) xe đi đi thay nhớt. Chọn D. Câu hỏi 14 : Một trường tổ chức cho khoảng từ \(400\)đến \(500\) học sinh đi tham quan bằng ô tô. Tính số học sinh của trường đi tham quan, biết rằng nếu xếp \(25\)em hay \(30\) em vào một xe thì vừa đủ không thừa ai.
Đáp án: D Phương pháp giải: Gọi \(x\) là số học sinh của trường đi tham quan. Từ đề bài ta có \(x\,\, \vdots \,\,25\,\,;\,\,x\,\, \vdots \,\,30\) suy ra \(x \in BC\left( {25\, ;\,\,30} \right)\). Tìm \(BCNN\left( {25 \,;\,\,30} \right)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC\left( {25\, ;\,\,30} \right)\). Kết hợp với điều kiện \(400 < x < 500\) để tìm \(x\) . Lời giải chi tiết: Gọi \(x\) là số học sinh của trường đi tham quan \(\left( {400 < x < 500} \right).\) Vì nếu xếp \(25\) em hay \(30\) em vào một xe thì vừa đủ không thừa ai nên ta có \(x\,\, \vdots \,\,25\,\,;\,\,x\,\, \vdots \,\,30\) suy ra \(x \in BC\left( {25\, ;\,\,30} \right)\). Ta có: \(25\, = {5^2}\,\,\,;\,\,\,\,\,\,\,\,\,\,30 = 2.3.5\,.\) \( \Rightarrow BCNN\left( {25 \,;\,\,30} \right) = {2.3.5^2} = 150\). \( \Rightarrow BC\left( {25\, ;\,\,30} \right) = \left\{ {0\,;\,\,150\,;\,\,300\,;\,\,450\,;\,\,600\,;\,\,\,...} \right\}\) Do đó: \(x \in \left\{ {\,150\,;\,\,300\,;\,\,450\,;\,\,600\,;\,\,\,...} \right\}\) Lại có \(400 < x < 500\) nên \(x = 450\). Vậy trường đó có \(450\) học sinh đi tham quan. Chọn D. Câu hỏi 15 : Hưởng ứng ngày hội đọc sách, học sinh khối \(6\) trường THCS Bế Văn Đàn đóng góp cho thư viện một số cuốn sách. Nếu xếp số sách đó thành từng bó \(10\) cuốn, \(12\) cuốn, \(18\) cuốn đều vừa đủ bó. Biết số sách trong khoảng \(200\) đến \(400\) cuốn. Tính số sách học sinh khối \(6\) đã đóng góp cho thư viện nhà trường.
Đáp án: C Phương pháp giải: Gọi \(x\) là số sách khối \(6\) đã đóng góp. \(\left( {x \in {\mathbb{N}^*}} \right).\) Từ đề bài ta có \(x\,\, \vdots \,\,10\,\,;\,\,x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,18\) suy ra \(x \in BC\left( {10\, ;\,\,12\,;\,\,18} \right)\). Tìm \(BCNN\left( {10\, ;\,\,12\,;\,\,18} \right)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC\left( {10\, ;\,\,12\,;\,\,18} \right)\). Kết hợp với điều kiện \(200 < {\rm{ }}x < 400\) để tìm \(x\) . Lời giải chi tiết: Gọi \(x\) là số sách khối \(6\) đã đóng góp \(\left( {200 < {\rm{ }}x < 400,\,\,\,x \in {\mathbb{N}^*}} \right).\) Vì xếp số sách đó thành từng bó \(10\) cuốn, \(12\) cuốn, \(18\) cuốn đều vừa đủ bó nên ta có \(x\,\, \vdots \,\,10\,\,;\,\,x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,18\) suy ra \(x \in BC\left( {10\, ;\,\,12\,;\,\,18} \right)\). Ta có: \(10\, = 2.5\,\,\,;\,\,\,\,\,\,\,\,\,\,12 = {2^2}.3\,\,\,;\,\,\,\,\,\,\,\,\,\,18 = {2.3^2}\) \( \Rightarrow BCNN\left( {10\, ;\,\,12\,;\,\,18} \right) = {2^2}{.3^2}.5 = 180\). \( \Rightarrow BC\left( {10\, ;\,\,12\,;\,\,18} \right) = \left\{ {0\,;\,\,180\,;\,\,360\,;\,\,540\,;\,\,720\,;\,\,\,...} \right\}\) Do đó: \(x \in \left\{ {\,180\,;\,\,360\,;\,\,540\,;\,\,720\,;\,\,\,...} \right\}\) Lại có \(200 < x < 400\) nên \(x = 360\). Vậy khối \(6\) đã đóng góp cho thư viện nhà trường \(360\) cuốn sách. Chọn C. Câu hỏi 16 : Học sinh khối \(6\) của một trường khi xếp hàng \(12\), hàng \(15\) hay hàng \(18\) thì đều vừa đủ hàng. Tính số học sinh khối \(6\) của trường đó, biết rằng số học sinh này nằm trong khoảng từ \(500\) đến \(600\) học sinh.
Đáp án: A Phương pháp giải: Gọi \(x\) là số học sinh của trường. \(\left( {x \in {\mathbb{N}^*}} \right).\) Từ đề bài ta có \(x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,15\,\, ;\,\,x\,\, \vdots \,\,18\) suy ra \(x \in BC\left( {12\, ;\,\,15\,;\,\,18} \right)\). Tìm \(BCNN\left( {12\,;\,\,15 \,;\,\,18} \right)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC\left( {12\,; \,\,15\, ;\,\,18} \right)\). Kết hợp với điều kiện \(500 < {\rm{ }}x < 600\) để tìm \(x\) . Lời giải chi tiết: Gọi \(x\) là số học sinh của trường \(\left( {500 < {\rm{ }}x < 600,\,\,\,x \in {\mathbb{N}^*}} \right).\) Vì khi xếp hàng \(12\), hàng \(15\) hay hàng \(18\) thì đều vừa đủ hàng nên ta có \(x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,15\,\, ;\,\,x\,\, \vdots \,\,18\) suy ra \(x \in BC\left( {12\, ;\,\,15\,;\,\,18} \right)\). Ta có: \(12 = {2^2}.3\,\,\,;\,\,\,\,\,\,\,\,\,\,15\, = 3.5\,\,\,;\,\,\,\,\,\,\,\,\,\,18 = {2.3^2}\) \( \Rightarrow BCNN\left( {12\,;\,\,15 \,;\,\,18} \right) = {2^2}{.3^2}.5 = 180\). \( \Rightarrow BC\left( {12\,;\,\,15 \,;\,\,18} \right) = \left\{ {0\,;\,\,180\,;\,\,360\,;\,\,540\,;\,\,720\,;\,\,\,...} \right\}\) Do đó: \(x \in \left\{ {\,180\,;\,\,360\,;\,\,540\,;\,\,720\,;\,\,\,...} \right\}\) Lại có \(500 < {\rm{ }}x < 600\) nên \(x = 540\). Vậy trường đó có \(540\) học sinh. Chọn A. Câu hỏi 17 : Một sọt cam có khoảng \(200\) đến \(250\) quả. Nếu xếp số cam này vào các đĩa loại \(10\) quả, đĩa loại \(12\) quả, đĩa loại \(15\) quả đều vừa đủ. Hỏi trong sọt có bao nhiêu quả cam?
Đáp án: B Phương pháp giải: Gọi \(x\) là số quả cam trong sọt. Từ đề bài ta có \(x\,\, \vdots \,\,10\,;\,\,x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,15\) suy ra \(x \in BC\left( {10\, ;\,\,12\,;\,\,15} \right)\). Tìm \(BCNN\left( {10\, ;\,\,12\,;\,\,15} \right)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC\left( {10\, ;\,\,12\,;\,\,15} \right)\). Kết hợp với điều kiện \(200 < x < 250\) để tìm \(x\) . Lời giải chi tiết: Gọi \(x\) là số quả cam trong sọt \(\left( {200 < x < 250,\,\,x \in \mathbb{N}} \right)\). Vì xếp số cam này vào các đĩa loại \(10\) quả, đĩa loại \(12\) quả, đĩa loại \(15\) quả đều vừa đủ nên ta có \(x\,\, \vdots \,\,10\,;\,\,x\,\, \vdots \,\,12\,\,;\,\,x\,\, \vdots \,\,15\) suy ra \(x \in BC\left( {10\, ;\,\,12\,;\,\,15} \right)\). Ta có: \(10\, = 2.5\,\,\,;\,\,\,\,\,\,\,\,\,\,12 = {2^2}.3\,\,\,;\,\,\,\,\,\,\,\,\,\,15\, = 3.5\,\) \( \Rightarrow BCNN\left( {10\,;\,\,12 \,;\,\,15} \right) = {2^2}.3.5 = 60\). \( \Rightarrow BC\left( {10\,;\,\,12 \,;\,\,15} \right) = \left\{ {0\,;\,\,60\,;\,\,120\,;\,\,180\,;\,\,240\,;\,\,300\,;\,\,\,...} \right\}\) Do đó: \(x \in \left\{ {60\,;\,\,120\,;\,\,180\,;\,\,240\,;\,\,300\,;\,\,\,...} \right\}\) Lại có \(200 < x < 250\) nên \(x = 240\). Vậy sọt cam có \(240\) quả cam. Chọn B. Câu hỏi 18 : Tìm số tự nhiên nhỏ nhất, biết rằng khi chia cho \(8,\,\,10,\,\,15,\,\,20\) được số dư theo thứ tự \(5,\,\,7,\,\,12,\,\,17.\)
Đáp án: B Phương pháp giải: Đưa bài toán về dạng tìm BC hoặc BCNN. Lời giải chi tiết: Gọi số tự nhiên cần tìm là \(a\,.\) Theo bài ra ta có: \(\left\{ \begin{array}{l}a - 5\,\, \vdots \,\,8\\a - 7\,\, \vdots \,\,10\\a - 12\,\, \vdots \,\,15\\a - 17\,\, \vdots \,\,20\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a - 5 + 8\,\, \vdots \,\,8\\a - 7 + 10\,\, \vdots \,\,10\\a - 12 + 15\,\, \vdots \,\,15\\a - 17 + 20\,\, \vdots \,\,20\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a + 3\,\, \vdots \,\,8\\a + 3\,\, \vdots \,\,10\\a + 3\,\, \vdots \,\,15\\a + 3\,\, \vdots \,\,20\end{array} \right.\) Mà \(a\) là số tự nhiên nhỏ nhất \( \Rightarrow \left( {a + 3} \right) \in BC\left( {8;10;15;20} \right)\) \(\left\{ \begin{array}{l}8 = {2^3}\\10 = 2.5\\15 = 3.5\\20 = {2^2}.5\end{array} \right. \Rightarrow BCNN\left( {8;10;15;20} \right) = {2^3}.3.5 = 120\) \(\begin{array}{l} \Rightarrow a + 3 = BCNN\left( {8;10;15;20} \right) = 120\\ \Rightarrow a = 120 - 3 = 117.\end{array}\) Vậy số tự nhiên \(a\) cần tìm là \(117\). Chọn B. Câu hỏi 19 : Tìm hai số tự nhiên nhỏ hơn \(56\), biết hiệu của chúng là \(28\)và ước chung lớn nhất của chúng là \(14.\)
Đáp án: B Phương pháp giải: +) Gọi hai số tự nhiên cần tìm là \(a{;^{}}b\) (Điều kiện) +) Áp dụng \(UCLN\left( {a,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = d.m\\b = d.n\end{array} \right.;\,\,\,\,\,UCLN\,\left( {m,n} \right) = 1,\,\,\,m,\,\,n \in {\mathbb{N}^*}.\) +) Tìm \(m\) và \(n\), suy ra \(a{;^{}}b\). Lời giải chi tiết: Gọi hai số tự nhiên cần tìm là \(a,\,\,b\,\,\left( {0 < b < a < 56} \right)\). Theo bài ra ta có: \(a - b = 28\) và \(UCLN\left( {a,\,\,b} \right) = 14.\) Từ \(UCLN\left( {a,\,\,b} \right) = 14 \Rightarrow \left\{ \begin{array}{l}a = 14n\\b = 14m\end{array} \right.\,\,\,\left( {m,\,\,n \in {\mathbb{N}^*}} \right).\) Mà ta lại có: \(a - b = 28 \Rightarrow 14n - 14m = 28 \Rightarrow 14\left( {n - m} \right) = 28 \Rightarrow n - m = 2\,\,\,\left( {n > 2} \right)\) Vì \(a < 56 \Rightarrow 14n < 56 \Rightarrow n < 4 \Rightarrow n \in \left\{ {1;2;3} \right\}\). Mà \(n > 2\) suy ra \(n = 3\). Với \(n = 3 \Rightarrow m = 1\). Do đó, cặp số \(a\) và \(b\) thỏa mãn điều kiện đề bài \(\left( {a;\,\,b} \right) = \left( {42;\,\,14} \right).\) Chọn B. Câu hỏi 20 : Tìm \(a,\,\,b \in {\mathbb{N}^*}\) biết \(\frac{a}{b} = \frac{3}{5}\) và \(BCNN\left( {a;\,\,b} \right) = 225.\)
Đáp án: A Phương pháp giải: +) Gọi \(UCLN\left( {a,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = d.m\\b = d.n\end{array} \right.;\,\,\,UCLN\,\left( {m,n} \right) = 1,\,\,\left( {m,\,\,n \in {\mathbb{N}^*}} \right).\) +) Áp dụng công thức: \(BCNN\left( {a,\,\,b} \right).UCLN\left( {a,\,\,b} \right) = ab \Rightarrow \left[ {a,\,\,b} \right] = ?\) +) Tìm \(m;\,\,n\) suy ra \(a{;^{}}b\). Lời giải chi tiết: Theo bài ra ta có \(a\) và \(b\) là hai số tự nhiên thỏa mãn : \(\frac{a}{b} = \frac{3}{5}\) và \(BCNN\left( {a;\,\,b} \right) = 225\) Gọi \(UCLN\left( {a,\,\,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = md\\b = nd\end{array} \right.,\,\,\left( {m,\,\,n} \right) = 1\) và \(m,\,\,n \in {\mathbb{N}^*}\). Theo bài ra: \(\frac{a}{b} = \frac{3}{5} \Rightarrow \frac{{md}}{{nd}} = \frac{3}{5} \Rightarrow \frac{m}{n} = \frac{3}{5} \Rightarrow m = 3;\,\,n = 5\) Ta có: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a,\,\,b} \right) = ab \Rightarrow BCNN\left( {a;\,\,b} \right) = \frac{{ab}}{{UCLN\left( {a;\,\,b} \right)}} = \frac{{md.nd}}{d} = mnd\) Mà \(BCNN\left( {a;\,\,b} \right) = 225\) nên \(mnd = 225 \Rightarrow 3.5.d = 225 \Rightarrow d = 15 \Rightarrow \left\{ \begin{array}{l}a = 3.15\\b = 5.15\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 45\\b = 75\end{array} \right.\). Vậy cặp số tự nhiên \(a\) và \(\,b\) cần tìm là \(45\) và \(45\). Chọn A. Câu hỏi 21 : Hai bạn Minh và Ngọc thường đến thư viện đọc sách. Minh cứ \(12\) ngày đến thư viện \(1\) lần, Ngọc \(15\) ngày một lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi sau ít nhất bao nhiêu ngày thì cả hai bạn lại cùng đến thư viện?
Đáp án: C Phương pháp giải: Gọi \(x\) là số ngày ít nhất để hai bạn lại cùng đến thư viện \(\left( {x \in {\mathbb{N}^*}} \right)\) . Theo đề bài ta có \(x = BCNN\left( {30\,;\,\,40} \right)\) Tìm \(BCNN\left( {30\,;\,\,40} \right)\) bằng cách phân tích các số ra thừa số nguyên tố. Lời giải chi tiết: Gọi \(x\) là số ít nhất để hai bạn lại cùng đến thư viện \(\left( {x \in {\mathbb{N}^*}} \right)\). Vì Minh cứ \(12\) ngày đến thư viện \(1\) lần, Ngọc \(15\) ngày một lần và \(x\) là số ngày ít nhất để hai bạn lại cùng đến thư viện nên suy ra \(x = BCNN\left( {12\,;\,\,15} \right)\). Ta có: \(12 = {2^3}.3\,\,\,; 15 = 3.5\) \( \Rightarrow BCNN\left( {12 \,;\,\,15} \right) = {2^2}.3.5 = 60\) Do đó \(x = 60\). Vậy ít nhất sau \(60\) ngày thì Minh và Ngọc lại cùng đến thư viện. Chọn C. Câu hỏi 22 : Ba lớp \(6A\,,\,\,6B\) và \(6C\) tham gia lao động trồng cây. Các lớp trồng được số cây như nhau. Mỗi học sinh lớp \(6A\) trồng được \(4\) cây, mỗi học sinh lớp \(6B\) trồng được \(5\) cây và mỗi học sinh lớp \(6C\) trồng được \(6\) cây. Tính số cây mỗi lớp trồng được, biết rằng số cây đó trong khoảng từ \(50\) đến \(100\).
Đáp án: A Phương pháp giải: Gọi \(x\) là số cây mỗi lớp trồng được \(\left( {x \in {\mathbb{N}^*},\,\,\,50 < x < 100} \right).\) Từ đề bài ta có \(x\,\, \vdots \,\,4\,\,;\,\,x\,\, \vdots \,\,5;\,\,x\,\, \vdots \,\,6\) suy ra \(x \in BC\left( {4\, ;\,\,5\,;\,\,6} \right)\). Tìm \(BCNN\left( {4\, ;\,\,5\,;\,\,6} \right)\) bằng cách phân tích các số ra thừa số nguyên tố, sau đó tìm \(BC\left( {4\, ;\,\,5\,;\,\,6} \right)\). Kết hợp với điều kiện \(50 < x < 100\) để tìm \(x\) . Lời giải chi tiết: Gọi \(x\) (cây) là số cây mỗi lớp trồng được. \(\left( {x \in {\mathbb{N}^*},\,\,\,50 < x < 100} \right).\) Mỗi học sinh lớp \(6A\) trồng được \(4\) cây, mỗi học sinh lớp \(6B\) trồng được \(5\) cây và mỗi học sinh lớp \(6C\) trồng được \(6\) cây và số học sinh của mỗi lớp là số tự nhiên nên ta có \(x\,\, \vdots \,\,4\,\,;\,\,x\,\, \vdots \,\,5;\,\,x\,\, \vdots \,\,6\) suy ra \(x \in BC\left( {4\,;\,\,5\,;\,\,6} \right)\). Ta có: \(4\, = {2^2}\,\,\,;\,\,\,\,\,\,\,\,\,\,5 = 5\,\,\,;\,\,\,\,\,\,\,\,\,\,6 = 2.3\) \( \Rightarrow BCNN\left( {4\, ;\,\,5\,;\,\,6} \right) = {2^2}.3.5 = 60\). \( \Rightarrow BC\left( {4\, ;\,\,5\,;\,\,6} \right) = \left\{ {0\,;\,\,60\,;\,\,120\,;\,\,180\,;\,\,240\,;\,\,\,...} \right\}\) Do đó: \(x \in \left\{ {60\,;\,\,120\,;\,\,180\,;\,\,240\,;\,\,\,...} \right\}\) Lại có \(50 < x < 100\) nên \(x = 60\). Vậy mỗi lớp trồng được \(60\) cây. Chọn A. Câu hỏi 23 : Một số sách sau khi xếp thành từng bó \(10\) cuốn, \(12\) cuốn, \(15\) cuốn, \(18\) cuốn đều thừa \(2\) cuốn. Tính số sách đó biết rằng số sách trong khoảng từ \(350\) đến \(400\) cuốn.
Đáp án: C Phương pháp giải: - Gọi số sách cần tìm là \(x\), tìm điều kiện của \(x\). - Sử dụng kiến thức về bội chung để tìm \(x\). Lời giải chi tiết: Gọi số sách cần tìm là \(x\) (cuốn sách) , \(350 \le x \le 400,\,\,x \in \mathbb{N}.\) Vì số sách xếp từng bó \(10,12,15\) cuốn đều thừa \(2\) cuốn nên \(\left( {x - 2} \right)\,\,\, \vdots \,\,10;\,\,\left( {x - 2} \right)\,\,\, \vdots \,\,\,12;\,\,\,\left( {x - 2} \right)\,\,\, \vdots \,\,15.\) Do đó \(x - 2 \in BC\left( {10,12,15} \right)\). Ta có: \(\left. \begin{array}{l}10 = 2.5\\12 = {2^2}.3\\15 = 3.5\end{array} \right\}\) \( \Rightarrow BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\) \( \Rightarrow BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,360;\,\,420;...} \right\}\) \( \Rightarrow x - 2 \in \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,\,360;\,\,420;...} \right\}\) Mà \(350 \le x \le 400\) nên \(348 \le x - 2 \le 398\) hay \(x - 2 = 360\) \( \Rightarrow x = 360 + 2 = 362\) cuốn. Vậy số sách cần tìm là \(362\) cuốn. Chọn C. Câu hỏi 24 : Số học sinh khối \(6\) của một trường trong khoảng từ \(300\) đến \(500\) học sinh. Biết rằng mỗi lần xếp hàng \(7\), hàng \(9\), hàng \(15\) đều thừa ra \(5\) học sinh. Tính số học sinh khối \(6\) của trường đó.
Đáp án: B Phương pháp giải: Gọi số học sinh khối 6 là \(x\,\left( {x > 5} \right)\) Ta suy ra \(\left( {x - 5} \right)\) là bội của \(7,9,15\) Từ đó đưa về bài toán tìm bội chung nhỏ nhất và bội chung Kết hợp với điều kiện bài toán để tìm \(x.\) Lời giải chi tiết: Gọi số học sinh khối 6 là \(x\,\,\,\left( {x > 5,x \in \mathbb{N}} \right)\)(học sinh). Từ đề bài suy ra \(\left( {x - 5} \right)\) là bội của \(7,9,15\) Hay \(x \in BC\left( {7;9;15} \right)\) và \(300 < x < 500\) Ta có : \(7 = 7;\,9 = {3^2};15 = 3.5\) Nên \(BCNN\left( {7;9;15} \right) = {7.3^2}.5 = 315\) Suy ra \(\left( {x - 5} \right) \in B\left( {315} \right) = \left\{ {0;315;630;...} \right\}\)hay \(x \in \left\{ {5;320;635;...} \right\}\) mà \(300 < x < 500\) nên \(x = 320\) Vậy số học sinh khối 6 là \(320\) học sinh. Chọn B. Câu hỏi 25 : Học sinh của một trường khi xếp thành \(18\) hàng, \(20\) hàng hoặc \(36\) hàng thì vừa đủ. Tính số học sinh của trường đó, biết rằng số học sinh đó trong khoảng từ \(700\) đến \(800\) em.
Đáp án: D Phương pháp giải: Lập luận để có số học sinh của trường là bội chung của \(18,20,36.\) Từ đó đưa về bài toán tìm bội chung thông qua bội chung nhỏ nhất. Kết hợp với điều kiện đề bài để kết luận số học sinh của trường đó. Lời giải chi tiết: Gọi \(x\,\,\left( {x \in {\mathbb{N}^*}} \right)\) là số học sinh của trường đó. Theo đề bài ta có : \(x\,\, \vdots \,\,18\,\,;\,\,\,\,\,x\,\, \vdots \,\,20\,\,;\,\,\,\,\,x\,\, \vdots \,\,36\). \( \Rightarrow x \in BC\left( {18;20;36} \right)\) Ta tìm bội chung thông qua bội chung nhỏ nhất. Ta có: \(18 = {2.3^2}\,\,;\,\,\,\,20 = {2^2}.5\); \(36 = {2^2}{.3^2}\) \(\begin{array}{l} \Rightarrow BCNN\left( {18;20;36} \right) = {2^2}{.3^2}.5 = 180\\ \Rightarrow BC\left( {18;20;36} \right) = \left\{ {0;180;360;540;720;960;...} \right\}\\ \Rightarrow x \in \left\{ {0;180;360;540;720;960;...} \right\}\end{array}\) Do \(700 < x < 800\) nên \(x = 720\). Vậy số học sinh của trường là \(720\) học sinh. Chọn D. Câu hỏi 26 : Tìm các số tự nhiên \(a\) và \(b\) biết: \(a.b = 360\) và \(BCNN(a,b) = 60\)
Phương pháp giải: Áp dụng công thức: BCNN \((a,b)\). ƯCLN \((a,b) = \,\,a.b\) để tìm ƯCLN \((a,b)\). Từ đó lập luận để tìm \(a\) và \(b\). Lời giải chi tiết:
Ta có: BCNN \((a,b)\). ƯCLN \((a,b) = \,\,a.b\) Thay \(a.b = 360\) và \(BCNN(a,b) = 60\) vào công thức trên ta có: \(60.\) ƯCLN \((a,b) = \,\,360\) \( \Rightarrow \) ƯCLN \((a,b) = \,\,360:60 = 6\) Giả sử \(a = 6x,\,\,b = 6y\). Do \(a.b = 360\) nên ta có: \(6x.6y = 360\), suy ra \(x.y = 10\) Lại có: \(10 = 1.10 = 2.5\) nên ta có bảng sau:
Do đó: \(\begin{array}{l} + )\,\,\,x = 1,\,\,y = 10 \Rightarrow a = 6.1 = 6\,;\,\,\,\,\,b = 6.10 = 60\\ + )\,\,\,x = 2,\,\,y = 5 \Rightarrow \,a = 6.2 = 12\,;\,\,\,\,\,b = 6.5 = 30\\ + )\,\,\,\,x = 5,\,\,y = 2 \Rightarrow a = 6.5 = 30\,;\,\,\,\,\,b = 6.2 = 12\\ + )\,\,\,\,x = 10,\,\,y = 1 \Rightarrow a = 6.10 = 60\,;\,\,\,\,\,b = 6.1 = 6\end{array}\) Vậy có \(4\) cặp giá trị \(a,\,\,b\) thỏa mãn đề bài là \(a = 6\) và \(b = 60\) ; \(a = 12\) và \(b = 30\); \(a = 30\) và \(b = 12\); \(a = 60\) và \(b = 6\).
Câu hỏi 27 : Biết \(BCNN\left( {a,b} \right) = 20.UCLN\left( {a,b} \right)\) và \(a.b = 180\). Tìm \(a\), \(b\).
Đáp án: D Phương pháp giải: Dạng bài: Tìm hai số \(a\) và \(b\) khi biết tích và biểu thức liên quan giữa \(BCNN\) và \(UCLN\). +) Xác định \(UCLN\left( {a,b} \right)\) từ Biều thức của đề bài và công thức \(BCNN\left( {a;b} \right).UCLN\left( {a;b} \right) = ab\) +) Bài toán về dạng tìm hai số khi biết \(UCLN\left( {a,b} \right)\) và \(a.b\). Lời giải chi tiết: Ta có: \(\left. \begin{array}{l}BCNN\left( {a,b} \right) = 20.UCLN\left( {a,b} \right)\\BCNN\left( {a,b} \right).UCLN\left( {a,b} \right) = ab = 180 \Rightarrow BCNN\left( {a,b} \right) = \frac{{180}}{{UCLN\left( {a,b} \right)}}\end{array} \right\}\)\( \Rightarrow \frac{{180}}{{UCLN\left( {a,b} \right)}} = 20.UCLN\left( {a,b} \right)\) \( \Rightarrow UCLN\left( {a,b} \right).UCLN\left( {a,b} \right) = 9\) \( \Rightarrow UCLN\left( {a,b} \right) = 3\)\( \Rightarrow \left\{ \begin{array}{l}a = 3.m\\b = 3.n\end{array} \right.\begin{array}{*{20}{c}}{}&{}\end{array}\left( {m,n} \right) = 1\) Mà \(a.b = 180 \Rightarrow 3.m.3.n = 180 \Rightarrow m.n = 20\). Kết hợp với \(m\) và \(n\) là hai số nguyên tố cùng nhau nên ta có: +) Với \(m = 4;n = 5 \Rightarrow a = 12;b = 15\). +) Với \(m = 5;n = 4 \Rightarrow a = 15;b = 12\). +) Với \(m = 1;n = 20 \Rightarrow a = 3;b = 60\). +) Với \(m = 20;n = 1 \Rightarrow a = 60;b = 3\). Vậy các cặp số \(\left( {a;b} \right)\) cần tìm là \(\left( {15;12} \right),\left( {12;15} \right),\left( {3;60} \right),\left( {60;3} \right).\) Chọn D. Câu hỏi 28 : Tìm hai số tự nhiên \(a\) và \(b\), biết \(UCLN\left( {a,b} \right) + BCNN\left( {a,b} \right) = 19\).
Đáp án: A Phương pháp giải: Dạng bài: Tìm hai số tự nhiên \(a\) và \(b\) khi biết tổng hoặc hiệu giữa \(UCLN\) và \(BCNN\). +) Đặt \(UCLN\left( {a,b} \right) = d\). Áp dụng công thức \(BCNN\left( {a;b} \right).UCLN\left( {a;b} \right) = ab\) suy ra \(BCNN\left( {a,b} \right) = \frac{{ab}}{{UCLN\left( {a,b} \right)}}\) +) Thay \(BCNN\left( {a,b} \right)\) và \(UCLN\left( {a,b} \right)\) vừa xác định được vào biểu thức của đề bài. Khi đó, tìm được \(d,m,n\). Lời giải chi tiết: Gọi \(d = UCLN\left( {a,b} \right) \Rightarrow \left\{ \begin{array}{l}a = d.m\\b = d.n\end{array} \right. \left( {m,n} \right) = 1,\,\,\,\left( {d,\,\,m,\,\,n \in {\mathbb{N}^*}} \right)\) Ta có: \(UCLN\left( {a,b} \right).BCNN\left( {a,b} \right) = ab \Rightarrow BCNN\left( {a,b} \right) = \frac{{ab}}{{UCLN\left( {a,b} \right)}} = \frac{{ab}}{d} = \frac{{d.m.d.m}}{d} = dmn\) Thay \(UCLN\left( {a,b} \right) = d\) và \(BCNN\left( {a,b} \right) = dmn\) vào \(UCLN\left( {a,b} \right) + BCNN\left( {a,b} \right) = 19\) ta được: \(d + dmn = 19 \Rightarrow d.\left( {1 + mn} \right) = 19\) +) Với \(d = 1 \Rightarrow 1 + mn = 19 \Rightarrow mn = 18\). Mà \(\left( {m,n} \right) = 1\) nên ta có bảng sau: +) Với \(d = 19 \Rightarrow 1 + mn = 1 \Rightarrow mn = 0\) (loại) Vậy các giá trị \(\left( {a;b} \right)\) cần tìm là \(\left( {2;9} \right),\left( {9;2} \right),\left( {1;18} \right),\left( {18;1} \right)\). Chọn A. Câu hỏi 29 : Tìm hai số tự nhiên \(a\) và \(b\) biết \(BCNN(a;\,\,b) - UCLN\left( {a,\,\,b} \right) = 35.\)
Đáp án: D Phương pháp giải: +) Gọi \(UCLN\left( {a,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = d.m\\b = d.n\end{array} \right.,\,\,\,UCLN\,\left( {m,n} \right) = 1,\,\,\left( {m,\,\,n \in {\mathbb{N}^*}} \right).\) +) Áp dụng CT: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a;\,\,b} \right) = ab \Rightarrow BCNN\left( {a;\,\,b} \right) = ...\) +) Tìm \(m;\,\,n\) suy ra \(a{;^{}}b\). Lời giải chi tiết: Gọi \(UCLN\left( {a,\,\,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = md\\b = nd\end{array} \right.,\,\,\,\,UCLN\left( {m,\,\,n} \right) = 1,\,\,m,\,\,n \in {\mathbb{N}^*}.\) Ta có: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a,\,\,b} \right) = ab \Rightarrow BCNN\left( {a;\,b} \right) = \frac{{ab}}{{UCLN\left( {a,\,\,b} \right)}} = \frac{{md.nd}}{d} = mnd\). Mặt khác: \(BCNN\left( {a;\,\,b} \right) - UCLN\left( {a,\,\,b} \right) = 35 \Rightarrow mnd - d = 35 \Rightarrow \left( {mn - 1} \right)d = 35\) \( \Rightarrow mn - 1 \in U\left( {35} \right) = \left\{ {1;5;7;35} \right\} \Rightarrow mn \in \left\{ {2;\,\,6;\,\,8;36} \right\}\) +) Với \(d = 1 \Rightarrow mn - 1 = 35 \Rightarrow mn = 36\) +) Với \(d = 5 \Rightarrow mn - 1 = 7 \Rightarrow mn = 8\) +) Với \(d = 7 \Rightarrow mn - 1 = 5 \Rightarrow mn = 6\) +) Với \(d = 35 \Rightarrow mn - 1 = 1 \Rightarrow mn = 2\) Vậy ta có các cặp số thỏa mãn bài toán là: \(\left( {a;\,\,b} \right) = \left\{ {\left( {1;\,36} \right),\,\,\left( {36;\,\,1} \right),\,\,\left( {4;\,\,9} \right),\,\,\left( {9;\,\,4} \right),\,\,\left( {5;\,\,40} \right),\,\,\left( {40;\,\,5} \right),\,\,\left( {7;\,\,42} \right),\,\,\left( {42;\,\,7} \right),\,\,\left( {14;\,\,21} \right),\,\,\left( {21;\,\,14} \right),\,\,\left( {35;\,\,70} \right),\,\,\left( {70;\,\,35} \right)} \right\}.\) Chọn D. Câu hỏi 30 : Tìm \(a,\,\,b \in \mathbb{N}\) thỏa mãn \(a + b = 28\) và \(UCLN\left( {a,\,\,b} \right) + 2BCNN\left( {a;\,\,b} \right) = 100.\)
Đáp án: C Phương pháp giải: +) Gọi \(UCLN\left( {a,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = d.m\\b = d.n\end{array} \right.\,\,,\,\,\,UCLN\,\left( {m,n} \right) = 1,\,\,\,m,\,\,n \in {\mathbb{N}^*}.\) +) Áp dụng công thức: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a;\,\,b} \right) = ab.\) Lời giải chi tiết: Gọi \(UCLN\left( {a,\,\,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = md\\b = nd\end{array} \right.,\,\,\,\,\left( {m,\,\,n} \right) = 1\,\) với \(m,\,\,n \in {\mathbb{N}^*}\). Theo bài ra ta có: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a,\,\,b} \right) = ab \Rightarrow BCNN\left( {a;\,\,b} \right) = \frac{{ab}}{{UCLN\left( {a,\,\,b} \right)}} = \frac{{md.nd}}{d} = mnd\) +) \(a + b = 28 \Rightarrow dm + dn = 28 \Rightarrow \left( {m + n} \right)d = 28\,\,\,\,\,\,\left( 1 \right) \Rightarrow d \in U\left( {28} \right)\) +) \(UCLN\left( {a,\,\,b} \right) + 2BCNN\left( {a;\,\,b} \right) = 100 \Rightarrow d + 2mnd = 100 \Rightarrow d\left( {1 + 2mn} \right) = 100\,\,\,\,\,\left( 2 \right) \Rightarrow d \in U\left( {100} \right)\) \( \Rightarrow d \in UC\left( {28,100} \right)\) Ta có: \(\left\{ \begin{array}{l}28 = {2^2}.7\\100 = {2^2}{.5^2}\end{array} \right. \Rightarrow UCLN\left( {28,100} \right) = {2^2} = 4\) \( \Rightarrow d \in UC\left( {28,100} \right) = U\left( 4 \right) = \left\{ {1;2;4} \right\}\) TH1: Với \(d = 1\) Từ \(\left( 1 \right)\) ta có: \(m + n = 28.\) Từ \(\left( 2 \right)\) ta có: \(1 + 2mn = 100 \Rightarrow 2mn = 99\) \( \Rightarrow \) Không có cặp số tự nhiên \(m,\,\,n\) thỏa mãn bài toán. TH2: Với \(d = 2\) Từ \(\left( 1 \right)\) ta có: \(m + n = 14.\) Từ \(\left( 2 \right)\) ta có: \(1 + 2mn = 50 \Rightarrow 2mn = 49\) \( \Rightarrow \) Không có cặp số tự nhiên \(m,\,\,n\) thỏa mãn bài toán. TH3: Với \(d = 4\) Từ \(\left( 1 \right)\) ta có: \(m + n = 7.\) Từ \(\left( 2 \right)\) ta có: \(1 + 2mn = 25 \Rightarrow 2mn = 24 \Rightarrow mn = 12.\) Vì \(m,\,\,n \in {\mathbb{N}^*},\,\,\,UCLN\left( {m,\,\,n} \right) = 1 \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m = 3\\n = 4\end{array} \right.\,\, \Rightarrow \left\{ \begin{array}{l}a = 4.3 = 12\\b = 4.4 = 16\end{array} \right.\\\left\{ \begin{array}{l}m = 4\\n = 3\end{array} \right.\,\, \Rightarrow \left\{ \begin{array}{l}a = 4.4 = 16\\b = 4.3 = 12\end{array} \right.\end{array} \right..\) Vậy cặp số thỏa mãn bài toán là:\(\left( {a;\,\,b} \right) = \left\{ {\left( {12;\,\,16} \right),\,\,\left( {16;\,\,12} \right)} \right\}.\) Chọn C.
|