30 bài tập trắc nghiệm xác suất của biến cố mức độ vận dụng caoLàm bàiCâu hỏi 1 : Trong giải cầu lông kỷ niệm ngày truyền thống học sinh sinh viên có 8 người tham gia trong đó có hai bạn Việt và Nam. Các vận động viên được chia làm hai bảng A và B, mỗi bảng gồm 4 người. Giả sử việc chia bảng thực hiện bằng cách bốc thăm ngẫu nhiên, tính xác suất để cả 2 bạn Việt và Nam nằm chung 1 bảng đấu.
Đáp án: D Phương pháp giải: Lời giải chi tiết: +) Gọi không gian mẫu là: “Chia 8 người vào 2 bảng A, B, mỗi bảng 4 người” ⇒nΩ=C48.C44=70 +) Gọi A là biến cố: “cả 2 bạn Việt và Nam nằm chung 1 bảng đấu”. ∙ TH1: Việt và Nam ở bảng A ⇒C26.C44=15 cách ∙ TH2: Việt và Nam ở bảng B ⇒C26.C44=15 cách ⇒nA=15+15=30 ⇒PA=nAnΩ=37 Chọn D. Câu hỏi 2 : Cho tập hợp A={0;1;2;3;4;5}. Gọi S là tập hợp các số có 3 chữ số khác nhau được lập thành từ các chữ số của tập A. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn có chữ số cuối gấp đôi chữ số đầu.
Đáp án: C Phương pháp giải: Lời giải chi tiết: Ω: Tập hợp S các số có 3 chữ số khác nhau được lập từ các chữ số của tập A. Số có 3 chữ số là ¯abc a có 5 cách chọn b có 5 cách chọn c có 4 cách chọn ⇒nΩ=5.5.4=100 Gọi A là biến cố: Số được chọn có chữ số cuối gấp đôi chữ số đầu ∙ TH1: {a=1c=2⇒ a có 1 cách chọn, c có 1 cách chọn ⇒ b có 4 cách chọn ⇒ Có: 1.1.4=4 cách ∙ TH1: {a=2c=4⇒ a có 1 cách chọn, c có 1 cách chọn ⇒ b có 4 cách chọn ⇒ Có: 1.1.4=4 cách ⇒nA=4+4=8 ⇒PA=nAnΩ=8100=225 Chọn C. Câu hỏi 3 : Cho tập hợp A={2;3;4;5;6;7;8}. Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập thành từ các chữ số của tập A. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn mà trong mỗi số luôn luôn có mặt hai chữ số chẵn và hai chữ số lẻ.
Đáp án: B Phương pháp giải: Lời giải chi tiết: Ω: Tập hợp S các số tự nhiên có 4 chữ số đôi một khác nhau được lập thành từ các chữ số của tập A. Số có 4 chữ số: ¯abcd a có 7 cách chọn b có 6 cách chọn c có 5 cách chọn d có 4 cách chọn ⇒nΩ=7.6.5.4=840 Biến cố A: Số được chọn có 2 chữ số chẵn và 2 chữ số lẻ. Số chẵn: {2;4;6;8} Số lẻ: {3;5;7} ∙ Số cách chọn chẵn: a có 4 cách chọn b có 3 cách chọn ∙ Số cách chọn lẻ: c có 3 cách chọn d có 2 cách chọn ⇒nA=4.3.3.2=72⇒PA=72840=335 Chọn B. Câu hỏi 4 : Gọi S là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau được lập thành từ các chữ số 1; 2; 3; 4; 6. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn chia hết cho 3.
Đáp án: C Phương pháp giải: Lời giải chi tiết: +) Ω: “Tập hợp các số tự nhiên có 3 chữ số khác nhau được lập thành từ các chữ số 1; 2; 3; 4; 6” ⇒nΩ=A35 số +) Để số đó chia hết cho 3 ⇔ Tổng các chữ số chia hết cho 3 ⇔A={(1;2;3);(1;2;6);(2;3;4);(2;4;6)} ⇒ Có 4 trường hợp, mỗi trường hợp có A33 cách sắp xếp ⇒nA=4.A33=24 số ⇒PA=24A35=25 Chọn C. Câu hỏi 5 : Một hộp đựng 10 chiếc thẻ được đánh số từ 0 đến 9. Lấy ngẫu nhiên ra 3 chiếc thẻ, tính xác suất để 3 chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5.
Đáp án: A Phương pháp giải: Lời giải chi tiết: +)Ω: “Lấy ngẫu nhiên 3 thẻ” ⇒nΩ=C310 +) Biến cố A: “3 chữ số trên 3 thẻ có thể ghép thành 1 số chia hết cho 5”. +) Số tự nhiên chia hết cho 5 cần có số tận cùng là 0 hoặc 5. ⇒ Phải rút được 1 trong 2 thẻ, hoặc cả 2 thẻ ⇒ Dùng biến cố đối là ¯A: “Rút ra 3 thẻ trong đó không có 0 và 5” ⇒n¯A=C38 ⇒P¯A=C38C310=715 ⇒PA=1−715=815 Chọn A. Câu hỏi 6 : Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
Đáp án: A Phương pháp giải: Lời giải chi tiết: +) Số tự nhiên có 2 chữ số là: C19.C110=90 số +)Ω: “Chọn ngẫu nhiên 2 số từ tập hợp S” ⇒nΩ=C290 +) A: “Chọn được 2 số có chữ số hàng đơn vị giống nhau”. ∙ TH1: Chữ số hàng đơn vị là 0 ⇒ Có 9 chữ số là: 10;20;30;40;50;60;70;80;90 ⇒ Số cách chọn 2 số là: C29 Tương tự với các số có chữ số hàng đơn vị là: 1;2;3;4;5;6;7;8;9 ⇒ Có tất cả 10 trường hợp giống nhau. ⇒nA=10.C29 ⇒PA=10.C29C290=889 Chọn A. Câu hỏi 7 : Trong một hộp có 50 viên bi được đánh số từ 1 đén 50. Chọn ngẫu nhiên 3 viên bi trong hộp, tính xác suất để tổng ba số trên 3 viên bi được chọn là một số chia hết cho 3
Đáp án: B Phương pháp giải: Lời giải chi tiết: + Gọi không gian mẫu là: “Lấy ngẫu nhiên 3 viên bi trong hộp” ⇒nΩ=C350 + Gọi A là biến cố: “Tổng 3 số ghi trên 3 viên bi là một số chia hết cho 3” + Nhận xét: Trong 50 viên bi ta phân ra làm 3 loại Loại 1: 16 viên bi có số chia hết cho 3 Loại 2: 17 viên bi có số chia 3 dư 1 Loại 3: 17 viên bi có số chia 3 dư 2 + Ta có: Tổng 3 số trên bi chia hết cho 3 nếu TH1: 3 bi chọn ra đều có số chia hết cho 3⇒ lấy ra 3 viên từ Loại 1 ⇒ C316 cách TH2: 3 bi chọn ra trong đó có: 1 bi chia hết cho 3 ⇒C116 1 bi chia cho 3 dư 1⇒C117 1 bi chia cho 3 dư 2⇒C117 (Chú ý: Khi cộng tổng lại thì số dư là 3⇒cũng chia hết cho 3) ⇒ C116.C117.C117 cách TH3: 3 bi chọn ra đều có số chia 3 dư 1: C317 (đều dư 1 vậy cộng tổng lại là dư 3 ⇒ cũng chia hết cho 3) TH4: 3 bi chọn ra đều có số chia 3 dư 2: C317( đều dư 2 vậy cộng tổng lại là dư 6 ⇒ cũng chia hết cho 3) ⇒P(A)=C316+C116.C117.C117+C317+C317C350=4091225 Chọn B. Câu hỏi 8 : Có 6 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngẫu nhiên vào 9 ghế thành một dãy. Tính xác suất để xếp được 3 học sinh lớp 12 xen kẽ giữa 6 học sinh lớp 11.
Đáp án: A Phương pháp giải: Lời giải chi tiết: +)nΩ=9! +) Gọi A “Biến cố xếp 3 học sinh lớp 12 xen kẽ giữa 6 học sinh lớp 11” ∙ Bước 1: Xếp 6 học sinh lớp 11 thành 1 dãy ⇒6! cách Khi đó, giữa 6 học sinh lớp 11 sẽ có 7 khoảng trống ( 5 khoảng ở giữa và 2 khoảng ở đầu) ∙ Bước 2: Xếp 3 học sinh lớp 12 vào 7 khoảng trống đó ⇒A37 cách ⇒n(A)=6!×A37 ⇒P(A)=6!.A379!=512. Chọn A. Câu hỏi 9 : Trong thư viện có 12 quyển sách gồm 3 quyển Toán giống nhau, 3 quyển Lý giống nhau, 3 quyển Hóa giống nhau và 3 quyển Sinh giống nhau. Có bao nhiêu cách xếp thành một dãy sao cho 3 quyển sach thuộc cùng 1 môn không được xếp liền nhau
Đáp án: A Phương pháp giải: Lời giải chi tiết: Số cách xếp 12 quyển sách thành 1 dãy là: nΩ=C312.C39.C36.C33 Xét biến cố P tồn tại trong dãy 3 quyển sách cùng môn đứng cạnh nhau. Gọi A, B, C, D lần lượt là biến cố 3 quyển sách Toán, Lý, Hóa, Sinh đứng cạnh nhau. Ta có: nA=nB=nC=nD=C110.C39.C36.C33 nA∩B=nA∩C=nA∩D=nB∩C=nB∩D=nC∩D=C18.C17.C36 nA∩B∩C=nA∩B∩D=nA∩C∩D=nB∩C∩D=C16.C15.C14 nA∩B∩C∩D=4! ⇒nP=nA∪B∪C∪D=nA+nB+nC+nD−(nA∩B+...+nC∩D)−(nA∩B∩C+...+nB∩C∩D)−nA∩B∩C∩D=60936 Vậy số cách xếp để 3 quyển sách cùng môn không đứng cạnh nhau là: nΩ−nP=308664cách Chọn A. Câu hỏi 10 : Xếp 6 học sinh nam và 4 học sinh nữ vào một bàn tròn 10 ghế. Tính xác suất để không có hai học sinh nữ ngồi cạnh nhau
Đáp án: B Phương pháp giải: Lời giải chi tiết: +) Gọi không gian mẫu là: “Xếp 6 nam và 4 nữa vào 1 bàn tròn 10 ghế”. ⇒nΩ=9! +) Gọi A là biến cố: “Không có 2 bạn nữ nào ngồi cạnh nhau”. ∙ Xếp 6 ghế quanh bàn cho 6 nam: ⇒5! cách ∙ Giữa 2 nam bất kì có khoảng trống xếp 4 nữ vào 4 trong 6 khoảng trống đó. ⇒A46 cách ⇒nA=5!.A46 ⇒PA=nAnΩ=542 Chọn B. Câu hỏi 11 : Giải bóng chuyền VTV Cup gồm 9 đội bóng tham dự, trong đó có 6 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C và mỗi bảng có 3 đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau
Đáp án: C Phương pháp giải: Lời giải chi tiết: +) Gọi không gian mẫu là: “Chia 9 đội bóng vào 3 bảng A, B, C”. ⇒nΩ=C39.C36.C33=1680 +) Gọi A là biến cố: “3 đội bóng của Việt Nam ở 3 bảng khác nhau”. ∙ Bảng A: 1 đội Việt Nam – 2 đội nước ngoài ⇒C13.C26=45 cách ∙ Bảng B: 1 đội Việt Nam – 2 đội nước ngoài ⇒C12.C24=12 cách ∙ Bảng C: 3 đội còn lại ⇒1 cách ⇒nA=45.12.1=540 ⇒PA=nAnΩ=928 Chọn C. Câu hỏi 12 : Có 13 học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc trong đó khối 12 có 8 học sinh nam và 3 học sinh nữ, khối 11 có 2 học sinh nam. Chọn ngẫu nhiên 3 học sinh bất kỳ để trao thưởng, tính xác suất để 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Đáp án: A Phương pháp giải: Lời giải chi tiết: +) Gọi KGM là “Chọn ngẫu nhiên 3 học sinh bất kì” ⇒nΩ=C313=286 +) Gọi A là biến cố: “3 học sinh được chọn có cả nam và 2 nữ đồng thời có cả khối 11 và khối 12” TH1: 1 học sinh nam lớp 11 – 2 học sinh nữ lớp 12 ⇒C12.C23=6 TH2: 1 học sinh nam lớp 11 - 1 học sinh nữ lớp 12 - 1 học sinh nam lớp 11⇒C12.C13.C18=48 TH3: 2 học sinh nam lớp 11 - 1 học sinh nữ lớp 12 ⇒C22.C13=3 Vậy n(A)=6+48+3=57 ⇒P(A)=57286 Chọn A. Câu hỏi 13 : Một chiếc hộp đựng 7 viên bi màu xanh, 6 viên bi màu đen, 5 viên bi mày đỏ, 4 viên bi màu trắng. Chọn ngẫu nhiên ra 4 viên bi, tính xác suất để lấy được ít nhất 2 viên bi cùng màu
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chú ý: Dùng biến cố đối, thay vì tìm ra các trường hợp để lấy ra ít nhất 2 viên bi cùng màu, ta sẽ đi tìm ra số cách lấy ra 4 viên bi không cùng màu. + Gọi không gian mẫu là: “Chọn ngẫu nhiên ra 4 viên bi” ⇒nΩ=C422 +) Gọi A là biến cố: “Lấy 4 viên bi không cùng màu” ⇒Trong 4 viên lấy ra có 1 xanh, 1 đen, 1 đỏ và 1 trắng ⇒n(A)=C17.C16.C15.C14=840 ⇒P(A)=nAnΩ=840C422=24209 + Xác suất để lấy được ít nhất 2 viên bi cùng màu là: P(¯A)=1−P(A)=1−24209=185209 Chọn B. Câu hỏi 14 : Một hộp đựng 8 quả cầu trắng, 12 quả cầu đen. Lần thứ nhất lấy ngẫu nhiên 1 quả cầu trong hộp, lần thứ 2 lấy ngẫu nhiên 1 quả cầu trong các quả cầu còn lại. Tính xác suất để kết quả của hai lần lấy được 2 quả cầu cùng màu
Đáp án: C Phương pháp giải: Lời giải chi tiết: + Gọi không gian mẫu là: “Lấy ngẫu nhiên ra 1 quả cầu, sau đó lấy ngẫu nhiên tiếp 1 quả cầu trong các quả cầu còn lại” ⇒ nΩ=C120.C119 + Gọi A là biến cố: “cả 2 lần lấy đều lấy được quả cầu cùng màu” TH1: 2 quả đều là màu trắng: Lần 1 lấy được 1 quả cầu trắng: C18 Lần 2 lấy được 1 quả cầu trắng: C17 ⇒C18.C17 cách TH2: 2 quả đều là màu đen: Lần 1 lấy được 1 quả màu đen: C112 Lần 2 lấy được 1 quả màu đen: C111 ⇒C112.C111 Xác suất để kết quả của 2 lần lấy được 2 quả cùng màu là: P(A)=C18.C17+C112.C111C120.C119=4795 Chọn C. Câu hỏi 15 : Một hộp chứa 12 viên bi kích thước như nhau, trong đó có 5 viên bi màu xanh được đánh số từ 1 đến 5; có 4 viên bi màu đỏ được đánh số từ 1 đến 4 và 3 viên bi màu vàng được đánh số từ 1 đến 3. Lấy ngẫu nhiên 2 viên bi từ hộp, tính xác suất để 2 viên bi được lấy vừa khác màu vừa khác số
Đáp án: D Phương pháp giải: Lời giải chi tiết: + Gọi không gian mẫu là: “Lấy ngẫu nhiên 2 viên bi từ hộp” ⇒nΩ=C212 + Gọi A là biến cố: “hai viên bi lấy được vừa khác màu vừa khác số”. TH1: Lấy 1 bi đỏ trong 4 bi đỏ, lấy 1 bi xanh trong 4 bi xanh (vì trùng số nên loại 1 bi xanh đi) ⇒ Số cách lấy một bi đỏ và một bi xanh là: C14.C14=16 TH2: Tương tự cách trên ta có số cách lấy một bi xanh và một bi vàng là: C13.C14=12 TH3: Số cách lấy một bi đỏ và một bi vàng là: C13.C13=9 ⇒n(A)=16+12+9=37 P(A)=n(A)n(Ω)=37C212=3766 Chọn D. Câu hỏi 16 : Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp, tính xác suất để 6 viên bi được lấy ra có đủ cả 3 màu
Đáp án: A Phương pháp giải: Lời giải chi tiết: Chú ý: Ta dùng biến cố đối, thay vì tìm ra cách lấy 6 viên có đủ 3 màu (quá nhiều Trường hợp), ta sẽ đi tìm ra 6 viên bi ko đủ 3 màu. +) Gọi không gian mẫu là: “Lấy ngẫu nhiên 6 viên bi trong 14 bi” ⇒nΩ=C614=3003 +)Gọi A là biến cố: “Lấy ra 6 bi không đủ 3 màu” ( chỉ có 1 màu hoặc 2 màu) TH1: 6 viên lấy ra chỉ có 2 màu Xanh và đỏ: C68=28 Xanh và vàng: C69−C66=83 (với C66 là số cách lấy 1 màu vàng) Đỏ và vàng: C611−C66=461 (với C66 là số cách lấy 1 màu vàng) TH2: 6 viên lấy ra chỉ có 1 màu vàng: C66=1 Vậy n(A)=28+83+461+1=573 ⇒P(A)=n(A)nΩ=5734003 ⇒P(¯A)=1−5734003=8101001 Chọn A. Câu hỏi 17 : Cần chọn ngẫu nhiên 5 học sinh trong một lớp học có 15 nam và 10 nữ để tham gia đồng diễn. Tính xác suất sao cho 5 học sinh được chọn có cả nam lẫn nữ và số học sinh nữ ít hơn số học sinh nam?
Đáp án: D Phương pháp giải: Lời giải chi tiết: +) Gọi KGM là “Chọn 5 học sinh” ⇒nΩ=C525=53130 +) Gọi A là biến cố: “Số học sinh nữ ít hơn nam” TH1: “Số cách lấy được 2 học sinh nữ và 3 học sinh nam” ⇒C110.C315=20475 cách TH2: “Số cách lấy được 1 học sinh nữ và 4 học sinh nam” ⇒C110.C415=13650 cách ⇒n(A)=20475+13650=34125⇒P(A)=3412553130=325506 Chọn D. Câu hỏi 18 : Một đội gồm 5 nam và 8 nữ. Lập một nhóm gồm 4 người hát tốp ca, tính xác suất để trong 4 người được chọn có ít nhất 1 nữ
Đáp án: A Phương pháp giải: Lời giải chi tiết: +) Gọi KGM là: “Chọn 4 người từ đội gồm 5 nam và 8 nữ” ⇒nΩ=C413=715cách +) Gọi A là biến cố: “Chọn 4 người trong đó có ít nhất 1 nữ” TH1: Số cách chọn 3 nam và 1 nữ: C35.C18=80cách TH2: Số cách chọn 2 nam và 2 nữ: C25.C28=280cách TH3: Số cách chọn 1 nam và 3 nữ: C15.C38=280cách TH4: Số cách chọn 4 nữ: C48=70 cách ⇒nA=80+280+280+70=710⇒PA=710715=142143 Chọn A. Câu hỏi 19 : Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng
Đáp án: B Phương pháp giải: Lời giải chi tiết: +) Gọi KGM: “Chọn ngẫu nhiên 5 viên bi trong hộp” ⇒nΩ=C518=8568 +) Gọi A là biến cố: “5 viên bi được chọn có đủ màu và bi đỏ bằng bi vàng” TH1: 1 đỏ, 1 vàng, 3 xanh C16.C17.C35=420 TH2: 2 đỏ, 2 vàng, 1 xanh C26.C27.C15=1575 ⇒n(A)=420+1575=1995⇒P(A)=19958568=95408 Chọn B. Câu hỏi 20 : Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Chọn ngẫu nhiên từ hộp 4 viên bi, tính xác suất để 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh
Đáp án: C Phương pháp giải: Lời giải chi tiết: +) Gọi KGM là: “Chọn ngẫu nhiên 4 viên bi” ⇒nΩ=C412=495 +) Gọi A là biến cố: “4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh” TH1: 1 xanh – 3 đỏ ⇒C14.C35=40 (Cách) TH2: 1 xanh - 2 đỏ - 1 vàng ⇒C14.C25.C13=120(Cách) TH3: 2 xanh - 2 đỏ: ⇒C24.C25=60(Cách) TH4: 3 xanh - 1 đỏ: ⇒C34.C15=20(Cách) ⇒nA=40+120+60+20=240⇒PA=240495=1633 Chọn C. Câu hỏi 21 : Có 3 bó hoa. Bó thứ nhất có 8 hoa hồng, bó thứ hai có 7 bông hoa ly, bó thứ ba có 6 bông hoa huệ. Chọn ngẫu nhiên 7 hoa từ ba bó hoa trên để cắm vào các lọ hoa, tính xác suất để trong 7 hoa được chọn có số hoa hồng bằng số hoa ly
Đáp án: D Phương pháp giải: Lời giải chi tiết: +) Gọi KGM “Chọn ngẫu nhiên 7 hoa từ 3 bó hoa” ⇒nΩ=C721=116280 +) Gọi A là biến cố: “Trong 7 bông hoa được chọn có số hoa hồng bằng số hoa ly” TH1: 1 hoa hồng – 1 hoa ly – 5 hoa huệ: ⇒C18.C17.C56=336 TH2: 2 hoa hồng – 2 hoa ly – 3 hoa huệ ⇒C28.C27.C36=11760 TH3: 3 hoa hồng- 3 hoa ly – 1 hoa huệ: ⇒C38.C37.C16=11760 ⇒n(A)=336+11760+11760=23856⇒P(A)=n(A)nΩ=9944845 Chọn D. Câu hỏi 22 : Chọn ngẫu nhiên hai số khác nhau từ 23 số nguyên dương đầu tiên, xác suất để chọn được hai số có tích là một số lẻ là:
Đáp án: C Phương pháp giải: - Tính số phần tử của không gian mẫu. - Tính số phần tử của biến cố. - Tính xác suất của biến cố. Lời giải chi tiết: Không gian mẫu là |Ω|=C223. Gọi A là biến cố: “Hai số được chọn có tích là một số lẻ”. Suy ra 2 số đó đồng thời là 2 số lẻ ⇒|ΩA|=C212. Vậy P=|ΩA||Ω|=C212C223=623. Chọn C. Câu hỏi 23 : Gọi S là tập các số tự nhiên có 8 chữ số. Lấy một số bất kì của tập S. Tính xác suất để lấy được số lẻ và chia hết cho 9.
Đáp án: D Phương pháp giải: - Tính tổng số các số có 8 chữ số. - Tính số các số lẻ có 8 chữ số chia hết cho 9. Lời giải chi tiết: n(Ω)=99999999−10000000+1=90000000. Gọi A là biến cố: “Lấy được số lẻ và chia hết cho 9” Số lẻ nhỏ nhất có 8 chữ số chia hết cho 9 là: 10000017. Số lẻ lớn nhất có 8 chữ số chia hết cho 9 là: 99999999. ⇒n(A)=(99999999−10000017):18+1=5000000. Vậy P(A)=500000090000000=118. Chọn D. Câu hỏi 24 : Gọi X là tập hợp các số tự nhiên có bốn chữ số phân biệt được lập bởi các chữ số 0,1,2,4,5,7,8. Chọn ngẫu nhiên một số từ X. Tính xác suất để số được chọn chia hết cho 4.
Đáp án: D Phương pháp giải: Số chia hết cho 4 là số có 2 chữ số tận cùng chia hết cho 4. Lời giải chi tiết: Từ tập X lập được số các số tự nhiên có 4 chữ số phân biệt là: A47−A36=720 số. ⇒n(Ω)=720. Gọi A là biến cố: “số được chọn chia hết cho 4”. Gọi số tự nhiên có 4 chữ số là ¯abcd(a≠0,a,b,c,d∈X). Số chia hết cho 4 là số có 2 chữ số tận cùng chia hết cho 4. ⇒¯cd∈{04;08;12;20;24;28;40;48;52;72;80;84}. TH1: ¯cd∈{04;08;20;40;80} (có chứa số 0) ⇒ có 5 cách chọn ¯cd. Ứng với mỗi cách chọn c,d có A25=20 cách chọn a,b. ⇒ có 5.20=100 số. TH2: ¯cd∈{12;24;28;48;52;72;84} (Không chứa số 0) ⇒ Có 7 cách chọn ¯cd. Ứng với mỗi cách chọn c,d có 4 cách chọn a (a≠0) và 4 cách chọn b. ⇒ Có 7.4.4=112 số. Do đó n(A)=100+112=212. Vậy P(A)=n(A)n(Ω)=212720=53180. Chọn D. Câu hỏi 25 : Có ba người thợ săn cùng bắn một con nai. Xác suất bắn trúng của mỗi người lân lượt là 0,6;0,8;0,9. Tính xác suất để có ít nhất hai người bắn trúng.
Đáp án: A Phương pháp giải: Cho hai biến cố A,B độc lập. Khi đó ta có: P(A.B)=P(A).P(B). Lời giải chi tiết: Giả sử xác suất bắn trúng của người thứ nhất là P(A1)=0,6. ⇒ Xác suất bắn không trúng của người thứ nhất là: P(¯A1)=1−0,6=0,4. Giả sử xác suất bắn trúng của người thứ hai là P(A2)=0,8. ⇒ Xác suất bắn không trúng của người thứ hai là: P(¯A2)=1−0,8=0,2. Giả sử xác suất bắn trúng của người thứ ba là P(A3)=0,9. ⇒ Xác suất bắn không trúng của người thứ ba là: P(¯A3)=1−0,9=0,1. Gọi biến cố A: ‘‘Có ít nhất hai người bắn trúng đích’’. ⇒P(A)=P(A1).P(A2).P(A3)+P(¯A1).P(A2).P(A3)+P(A1).P(¯A2).P(A3)+P(A1).P(A2).P(¯A3)=0,6.0,8.0,9+0,4.0,8.0,9+0,6.0,2.0,9+0,6.0,8.0,1=0,876. Chọn A. Câu hỏi 26 : Gọi S là tập hợp các số tự nhiên gồm 3 chữ số phân biệt được chọn từ các chữ số {0;1;2;3;4;5;6}. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn có chữ số hàng đơn vị gấp đôi chữ số hàng trăm là:
Đáp án: A Phương pháp giải: - Tính số phần tử của không gian mẫu. - Tính số phần tử của biến cố. - Tính xác suất của biến cố. Lời giải chi tiết: Đặt A={0;1;2;3;4;5;6}. Gọi số có 3 chữ số là ¯abc(a≠0;a;b;c∈A). Số các số có 3 chữ số phân biệt được lập từ tập A là A37−A26=180. ⇒n(Ω)=C1648=648. Gọi X là biến cố: “số được chọn có chữ số hàng đơn vị gấp đôi chữ số hàng trăm”. ⇒¯ac∈{12;24;36}⇒ Có 3 cách chọn ¯ac. Số cách chọn b là 5 cách. ⇒n(X)=3.5=15. Vậy P(X)=n(X)n(Ω)=15180=112. Chọn A. Câu hỏi 27 : Cho một bảng gồm 9 ô vuông đơn vị như hình vẽ bên. Một em bé cầm 4 hạt đậu đặt ngẫu nhiên vào 4 ô vuông đơn vị trong bảng. Xác suất để bất kì hàng nào và cột nào của bảng cũng có hạt đậu bằng:
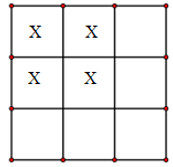
Đáp án: D Phương pháp giải: Lời giải chi tiết: Không gian mẫu: n(Ω)=C49=126. Gọi A là biến cố: “bất kì hàng nào và cột nào của bảng cũng có hạt đậu”, khi đó ta có biến cố đối: ¯A: “có 1 hàng hoặc 1 cột không có hạt đậu”. Gọi B là biến cố: 1 hàng không có đậu. - Chọn 1 hàng trong 3 hàng có C13 cách. - Xếp 4 hạt đậu vào 2 hàng còn lại có C46 cách. ⇒ n(B)=C13.C46=45 cách. Gọi C là biến cố: 1 cột không có đậu. - Chọn 1 cột trong 3 cột có C13 cách. - Xếp 4 hạt đậu vào 2 cột còn lại có C46 cách. ⇒ n(C)=C13.C46=45 cách. Ta có: B∩C = “1 hàng không có đậu và 1 cột không có đậu”.
- Chọn 1 hàng không có đậu có C13 cách. - Chọn 1 cột không có đậu có C13 cách. - Xếp 4 hạt đậu vào 4 ô còn lại có 1 cách. ⇒n(B∩C)=9. ⇒n(A)=n(B)+n(C)−n(B∩C)=45+45−9=81. Vậy P(A)=1−P(ˉA)=1−81126=514. Chọn D. Câu hỏi 28 : Một hộp đựng 9 thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên 2 thẻ và nhân hai số ghi trên thẻ với nhau. Tính xác suất để tích hai số trên 2 thẻ được rút ra là số chẵn?
Đáp án: B Phương pháp giải: - Tính số phần tử của không gian mẫu. - Gọi A là biến cố: “tích hai số trên 2 thẻ được rút ra là số chẵn”, suy ra biến cố đối ¯A. - Tính số phần tử của biến cố đối và xác suất của biến cố đối. - Sử dụng công thức P(A)=1−P(¯A). Lời giải chi tiết: Rút ngẫu nhiên 2 thẻ ⇒n(Ω)=C29. Gọi A là biến cố: “tích hai số trên 2 thẻ được rút ra là số chẵn” ⇒ Ít nhất 1 trong hai thẻ phải là số chẵn. ⇒ Biến cố đổi ¯A: “Không có thẻ nào là số chẵn” ⇒ Cả 2 thẻ đều là số lẻ. Số cách chọn 2 số lẻ từ 9 số từ 1 đến 9 là C25 ⇒n(¯A)=C25. Khi đó ta có P(¯A)=C25C29=518. Vậy P(A)=1−P(¯A)=1−518=1318. Chọn B. Câu hỏi 29 : Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C thành một hàng ngang. Xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau bằng:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Số cách xếp 10 học sinh vào 10 vị trí: n(Ω)=10! cách. Gọi A là biến cố: “Trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau”. Sắp xếp 5 học sinh lớp 12C vào 5 vị trí, có 5! cách. Ứng mỗi cách xếp 5 học sinh lớp 12C sẽ có 6 khoảng trống gồm 4 vị trí ở giữa và hai vị trí hai đầu để xếp các học sinh còn lại.
· TH1: Xếp 3 học sinh lớp 12B vào 4 vị trí trống ở giữa (không xếp vào hai đầu), có A34 cách. Ứng với mỗi cách xếp đó, chọn lấy 1 trong 2 học sinh lớp 12A xếp vào vị trí trống thứ 4 (để hai học sinh lớp 12C không được ngồi cạnh nhau), có 2 cách. Học sinh lớp 12A còn lại có 8 vị trí để xếp, có 8 cách. Theo quy tắc nhân, ta có 5!.A34.2.8 cách. · TH2: Xếp 2 trong 3 học sinh lớp 12B vào 4 vị trí trống ở giữa và học sinh còn lại xếp vào hai đầu, có C13.2.A24 cách. Ứng với mỗi cách xếp đó sẽ còn 2 vị trí trống ở giữa, xếp 2 học sinh lớp 12A vào vị trí đó, có 2 cách. Theo quy tắc nhân, ta có 5!.C13.2.A24.2 cách. Do đó số cách xếp không có học sinh cùng lớp ngồi cạnh nhau là n(A)=5!.A34.2.8+5!.C13.2.A24.2=63360 cách. Vậy P(A)=n(A)n(Ω)=6336010!=11630. Chọn A. Câu hỏi 30 : Một hộp chứa 6 viên bi đỏ, 5 viên bi vàng và 4 viên bi xanh. Lấy ngẫu nhiên 4 viên bi. Tính xác suất để 4 viên bi được lấy ra có đủ ba màu và không có hai viên nào có số thứ tự trùng nhau.
Đáp án: B Phương pháp giải: Xác suất của biến cố A là: P(A)=n(A)n(Ω). Lời giải chi tiết: Số phần tử của không gian mẫu: n(Ω)=C415=1365 Có 3 trường hợp sau: +) Chọn lần lượt theo thứ tự: 1 xanh, 1 vàng, 2 đỏ (loại bỏ bi có số thứ tự đã trùng của các viên đã chọn): C14.C14.C24=96 +) Chọn lần lượt theo thứ tự: 1 xanh, 2 vàng, 1 đỏ (loại bỏ bi có số thứ tự đã trùng của các viên đã chọn): C14.C24.C13=72 +) Chọn lần lượt theo thứ tự: 2 xanh, 1 vàng, 1 đỏ (loại bỏ bi có số thứ tự đã trùng của các viên đã chọn): C24.C13.C13=54 ⇒n(A)=96+72+54=222⇒P(A)=2221365=74455. Chọn B.
|