Phương pháp giải:

Thay số vào quy tắc đề bài cho.

Lời giải chi tiết:

Theo quy tắc ta có \(\left\{ \begin{array}{l}x' = {x_M} - 1 = 1 - 1 = 0\\y' = {y_M} + 2 = 2 + 2 = 4\end{array} \right. \Rightarrow A'\left( {0;4} \right).\)

Chọn D.

Phương pháp giải:

Điểm bất động qua phép biến hình là điểm mà có ảnh qua phép biến hình đó là chính nó.

Lời giải chi tiết:

Ta nói M là điểm bất động qua phép biến hình f  nghĩa là: \(f\left( M \right) = M\).

Chọn C.

Phương pháp giải:

\({T_{\overrightarrow u }}\) biến \(M\left( {x;y} \right)\) thành \(M'\left( {x';y'} \right) \Rightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).

Lời giải chi tiết:

\({T_{\overrightarrow v }}\left( A \right) = A' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 2 = 3\\{y_{A'}} = 3 + 3 = 6\end{array} \right. \Rightarrow A'\left( {3;6} \right)\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Chọn \(A\left( { - 1;0} \right) \in d:3x - 5y + 3 = 0\)

Tọa độ điểm \(A'\)  là ảnh của \(A\) qua \({T_{\overrightarrow v }}\) là: \(\left\{ \begin{array}{l}x' =  - 1 - 2 =  - 3\\y' = 0 + 3 = 3\end{array} \right.\)\( \Rightarrow A'\left( { - 3;3} \right).\)

Phương trình đường thẳng có dạng: \(3x - 5y + c = 0\)

Thay \(3x - 5y + c = 0\) vào \(d'\) ta có: \( - 9 - 15 + c = 0\)\( \Leftrightarrow c = 24\).

Vậy phương trình đường thẳng \(d'\) là:  \(3x - 5y + 24 = 0.\)

Chọn C.

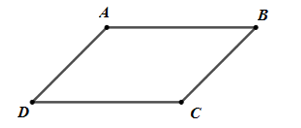
Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}A\left( {x;y} \right);\,\,M\left( {3;2} \right);\,\,\overrightarrow u \left( {2; - 1} \right)\\M = {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_A} = 3 - 2 = 1\\{y_A} = 2 - \left( { - 1} \right) = 3\end{array} \right. \Rightarrow A\left( {1; 3} \right)\end{array}\)

Chọn B.

Phương pháp giải:

Sử dụng định nghĩa phép tịnh tiến: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow v \).

Lời giải chi tiết:

Do \(ABCD\) là hình bình hành nên \(\overrightarrow {AB}  = \overrightarrow {DC}  \Rightarrow {T_{\overrightarrow {AB} }}\left( D \right) = C\).

Chọn B.

Phương pháp giải:

Sử dụng biểu thức tọa độ của phép tịnh tiến.

\({T_{\overrightarrow v }}\left( M \right) = M'\) với \(M\left( {x;y} \right);\,\,M'\left( {x';y'} \right);\,\,\overrightarrow v \left( {a;b} \right)\) thì \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).

Lời giải chi tiết:

Ta có \(\left\{ \begin{array}{l}x' = x - 2\\y' = y + 4\end{array} \right. \Rightarrow \overrightarrow v  = \left( { - 2;4} \right)\).

Chọn A.

Phương pháp giải:

Phép tịnh tiến theo \(\overrightarrow 0 \) là phép đồng nhất, tức là \({T_{\overrightarrow 0 }}\left( M \right) = M\).

Lời giải chi tiết:

\(\left\{ \begin{array}{l}{T_{\overrightarrow 0 }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = 0\\{T_{\overrightarrow 0 }}\left( N \right) = N' \Leftrightarrow \overrightarrow {NN'}  = 0\end{array} \right. \Rightarrow \overrightarrow {MM'}  = \overrightarrow {NN'}  = \overrightarrow 0 \).

Chọn C.

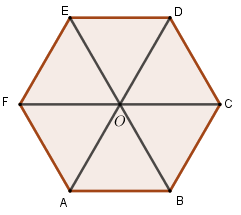
Phương pháp giải:

Dựng hình, tìm ảnh của \(O\) qua phép tịnh tiến theo véc tơ \(\overrightarrow {BO} \).

Sử dụng định nghĩa: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow v \).

Lời giải chi tiết:

Quan sát hình vẽ ta thấy \({T_{\overrightarrow {BO} }}\left( O \right) = E\) vì \(\overrightarrow {OE}  = \overrightarrow {BO} \).

Chọn C

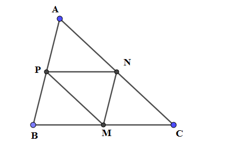
Phương pháp giải:

Sử dụng tính chất của phép tịnh tiến: Phép tịnh tiến biến một đườn tghẳng thành đường thẳng song song hoặc trùng với nó.

Lời giải chi tiết:

Ta có \(\dfrac{2}{1} \ne \dfrac{3}{{ - 1}} \Rightarrow {d_1}\) và \({d_2}\) cắt nhau.

Do đó không có phép tịnh tiến nào biến đường thẳng \({d_1}\) thành \({d_2}\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Phát biểu SAI là: Phép tịnh tiến theo vectơ \(\overrightarrow {BP} \) biến tam giác PMN thành tam giác APN.

Chọn: D

Phương pháp giải:

Biểu thức tọa độ của phép tịnh tiến theo \(\overrightarrow v \left( {a;b} \right)\) là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).

Lời giải chi tiết:

\(M = {T_{\overrightarrow v }}\left( N \right) \Rightarrow M\left( {5 - 3; - 3 + 5} \right) \Rightarrow N\left( {2;2} \right)\).

Chọn D.

Phương pháp giải:

Sử dụng khái niệm phép tịnh tiến.

Lời giải chi tiết:

Hai đường thẳng cắt nhau d và d’ \( \Rightarrow \) Không có phép tịnh tiến biến đường thẳng d thành đường thẳng d’.

Chọn: D

Phương pháp giải:

\({T_{\overrightarrow u }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow u \)

Lời giải chi tiết:

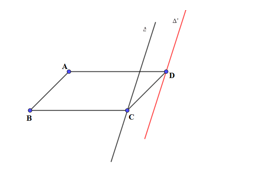
Ta có \(\overrightarrow {DA}  = \overrightarrow {CB}  \Rightarrow {T_{\overrightarrow {DA} }}\left( C \right) = B\).

Chọn đáp án B.

Phương pháp giải:

Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.

Lời giải chi tiết:

Điểm D di động trên đường thẳng \(\Delta '\) là ảnh của \(\Delta \) qua phép tịnh tiến theo \(\overrightarrow {BA} \).          

Chọn: B

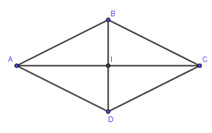
Phương pháp giải:

Phép tịnh tiến theo \(\overrightarrow{v}\) biến điểm M thành M’ \(\Leftrightarrow \overrightarrow{MM'}=\overrightarrow{v}\)

Lời giải chi tiết:

Phép tịnh tiến biến (O; R) thành chính nó là phép tịnh tiến theo vector \(\overrightarrow{0}\).

Chọn D.

Phương pháp giải:

Phép tịnh tiến theo vectơ \(\overrightarrow v \) biến điểm M thành điểm M’ thỏa mãn: \(\overrightarrow {MM'}  = \overrightarrow v \).

Lời giải chi tiết:

Ta có: \(\overrightarrow {IA}  = \overrightarrow {CI}  \Rightarrow \) Phép tịnh tiến theo vectơ \(\overrightarrow {IA} \) biến điểm C thành điểm I.

Chọn: A

Phương pháp giải:

Sử dụng khái niệm và các tính chất của phép tịnh tiến.

Lời giải chi tiết:

Chọn: C

Phương pháp giải:

- Vì \(\Delta '\parallel \Delta \) nên phương trình \(\Delta '\) có dạng: \(x + y + c = 0\).

- Chọn điểm A bất kì thuộc \(\Delta \), tìm ảnh A’ của A qua phép tịnh tiến theo vectơ \(\overrightarrow v \left( {2;1} \right)\).

- Thay tọa độ điểm A’ vào phương trình đường thẳng \(\Delta '\) tìm c.

Lời giải chi tiết:

Ta có: \({T_{\overrightarrow v }}\left( \Delta  \right) = \Delta ' \Rightarrow \) \(\Delta '\parallel \Delta \) nên phương trình \(\Delta '\) có dạng: \(x + y + c = 0\).

Chọn \(A\left( {1;0} \right) \in \Delta \), gọi \(A' = {T_{\overrightarrow v }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 2 = 3\\{y_{A'}} = 0 + 1 = 1\end{array} \right. \Rightarrow A'\left( {3;1} \right)\).

Vì \(A' \in \Delta ' \Rightarrow 3 + 1 + c = 0 \Leftrightarrow c =  - 4\).

Vậy phương trình \(\Delta ':\,\,x + y - 4 = 0\).

Chọn B.

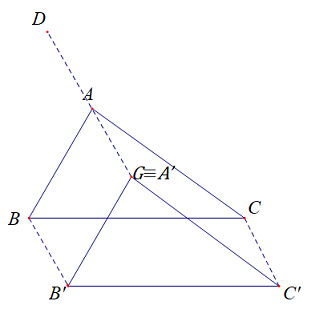
Phương pháp giải:

- Xác định tâm I và bán kính R của đường tròn (C).

- Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\), tìm tọa độ I’.

- Đường tròn (C’) là ảnh của (C) có tâm I’ và bán kính R, viết phương trình đường tròn.

Lời giải chi tiết:

Đường tròn (C) có tâm I(2;-1), bán kính \(R = \sqrt {4 + 1 - 1}  = 2.\)

Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\), ta có \(\left\{ \begin{array}{l}{x_{I'}} = 2 + 1 = 3\\{y_{I'}} =  - 1 + 3 = 2\end{array} \right. \Rightarrow I'\left( {3;2} \right)\).

Vì (C’) là ảnh của (C) qua phép tịnh tiến theo \(\overrightarrow v \left( {1;3} \right)\) nên (C’) là đường tròn có tâm I’(3;2), bán kính R’ = R = 2.

Vậy phương trình đường tròn (C’) là: \(\left( {C'} \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 4\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

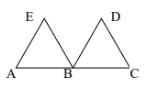
\( + )\) Xét \(\Delta ABC\): \(\left\{ \begin{array}{l}{T_{\overrightarrow {AG} }}\left( A \right) = A' \Rightarrow A' \equiv G\\{T_{\overrightarrow {AG} }}\left( B \right) = B' \Rightarrow \overrightarrow {BB'}  = \overrightarrow {AG} \\{T_{\overrightarrow {AG} }}\left( C \right) = C' \Rightarrow \overrightarrow {CC'}  = \overrightarrow {AG} \end{array} \right.\)                                           

\( + )\)\({T_{\overrightarrow {AG} }}\left( D \right) = A \Rightarrow \overrightarrow {DA}  = \overrightarrow {AG} \)                       

\( \Rightarrow \)\(D,\,\,A,\,\,G\)thẳng hàng.                    

Và \(A\) là trung điểm của \(DG\).

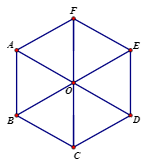
Phương pháp giải:

Lời giải chi tiết:

Phép tịnh tiến theo \(\overrightarrow {AB} \) hoặc \(\overrightarrow {BC} \), \(\overrightarrow {ED} \) biến \(A,\,\,B,\,\,E\) theo thứ tự thành 3 điểm \(B,\,\,C,\,\,D\).

Phương pháp giải:

Xác định ảnh của từng điểm qua phép tịnh tiến.

Lời giải chi tiết:

\(\begin{array}{l}{T_{\overrightarrow {BC} }}\left( A \right) = O\,\,do\,\,\overrightarrow {AO}  = \overrightarrow {BC} \\{T_{\overrightarrow {BC} }}\left( B \right) = C\\{T_{\overrightarrow {BC} }}\left( O \right) = D\,\,do\,\,\overrightarrow {OD}  = \overrightarrow {BC} \\{T_{\overrightarrow {BC} }}\left( F \right) = E\,\,do\,\,\overrightarrow {FE}  = \overrightarrow {BC} \end{array}\)

Vậy \({T_{\overrightarrow {BC} }}\left( {ABOF} \right) = OCDE\).

Chọn D.

Phương pháp giải:

Xác định tâm \(I\) của đường tròn \(\left( C \right)\)  

Sử dụng biểu thức tọa độ của phép tịnh tiến theo véc tơ \(\overrightarrow v  = \left( {a;b} \right)\) biến \(M\left( {x;y} \right)\) thành \(M'\left( {x';y'} \right)\) thì \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;1} \right)\)

Ảnh của  \(I\left( {0;1} \right)\) qua tịnh tiến theo vectơ \(\overrightarrow v \left( {3; - 2} \right)\) là \(I'\left( {x';y'} \right)\) là tâm của đường tròn \(\left( {C'} \right)\)

Khi đó: \(\left\{ \begin{array}{l}x' = 0 + 3 = 3\\y' = 1 + \left( { - 2} \right) =  - 1\end{array} \right. \Rightarrow I'\left( {3; - 1} \right)\)

Chọn C.

Phương pháp giải:

Áp dụng tính chất của phép tịnh tiến điểm M thành M’ theo vecto v thì \(\overrightarrow {MM'}  = \overrightarrow v \).

Lời giải chi tiết:

Đường tròn (C): \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\)có tâm I(1;-2); bán kinh R=3.

Gọi I’ là tâm đường tròn (C’).

Phép tịnh tiến điểm I thành điểm I’ theo véc-tơ \(\overrightarrow v \left( {3;3} \right)\)thì \(\overrightarrow {II'}  = \overrightarrow v \)

Suy ra \(I'\left( {4;1} \right)\)

Đường tròn (C’) có tâm là \(I'\left( {4;1} \right)\); R=3 nên có dạng \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\)

Chọn A.

Phương pháp giải:

Sử dụng định nghĩa về phép tịnh tiến trong mặt phẳng.

Lời giải chi tiết:

Gọi \(M\left( {x;y} \right) \in \Delta ;{T_{\overrightarrow u }}\left( M \right) = M'\left( {x';y'} \right) \in \Delta '\)

\( \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right. \Rightarrow M\left( {x' + 1;y' - 2} \right) \in d\)

\(M \in d \Rightarrow 2\left( {x' + 1} \right) - 3\left( {y' - 2} \right) - 5 = 0 \Leftrightarrow 2x' - 3y' + 3 = 0\)

Vậy phương trình ảnh của đường thẳng \(\Delta \) là: \(\Delta ' = 2x - 3y + 3 = 0\).

Chọn D.

Phương pháp giải:

\({T_{\overrightarrow u }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow u \).

Lời giải chi tiết:

Ta có \(\overrightarrow {AA'}  = \left( {1; - 2} \right)\). Vì \({T_{\overrightarrow u }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'}  = \overrightarrow u  = \left( {1; - 2} \right)\), do đó các đáp án C, D sai.

\(\begin{array}{l}{T_{\overrightarrow u }}\left( B \right) = B' \Leftrightarrow \overrightarrow {BB'}  = \overrightarrow u  \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - 2 = 1\\{y_{B'}} - 3 =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = 3\\{y_{B'}} = 1\end{array} \right. \Rightarrow B'\left( {3;1} \right)\\{T_{\overrightarrow u }}\left( C \right) = C' \Leftrightarrow \overrightarrow {CC'}  = \overrightarrow u  \Rightarrow \left\{ \begin{array}{l}{x_{C'}} - 6 = 1\\{y_{C'}} - 7 =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{C'}} = 7\\{y_{C'}} = 5\end{array} \right. \Rightarrow C'\left( {7;5} \right)\end{array}\)

Vậy đáp án B đúng.

Chọn B.

Phương pháp giải:

- Sử dụng định nghĩa phép tịnh tiến tìm tọa độ các điểm A’, B’, C’.

- Gọi H(a;b), giải hệ phương trình \(\left\{ \begin{array}{l}\overrightarrow {HA'} .\overrightarrow {B'C'}  = 0\\\overrightarrow {HB'} .\overrightarrow {A'C'}  = 0\end{array} \right.\) để tìm tọa độ điểm H.

Lời giải chi tiết:

Ta có: \(\overrightarrow {BC}  = \left( { - 6; - 2} \right)\).

\(\begin{array}{l}{T_{\overrightarrow {BC} }}\left( A \right) = A'\left( { - 5;2} \right)\\{T_{\overrightarrow {BC} }}\left( B \right) = B' \equiv C \Rightarrow B'\left( { - 2; - 2} \right)\\{T_{\overrightarrow {BC} }}\left( C \right) = C'\left( { - 8; - 4} \right)\end{array}\)

Gọi H(a;b;c) là trực tâm của tam giác A’B’C’, khi đó ta có \(HA' \bot B'C',\,\,HB' \bot A'C'\).

Do đó \(\left\{ \begin{array}{l}\overrightarrow {HA'} .\overrightarrow {B'C'}  = 0\\\overrightarrow {HB'} .\overrightarrow {A'C'}  = 0\end{array} \right.\).

Ta có:

\(\begin{array}{l}\overrightarrow {HA'}  = \left( { - 5 - a;2 - b} \right),\,\,\overrightarrow {B'C'}  = \left( { - 6; - 2} \right)\\\overrightarrow {HB'}  = \left( { - 2 - a; - 2 - b} \right),\,\,\overrightarrow {A'C'}  = \left( { - 3; - 6} \right)\\ \Rightarrow \left\{ \begin{array}{l}\left( { - 5 - a} \right).\left( { - 6} \right) + \left( {2 - b} \right).\left( { - 2} \right) = 0\\\left( { - 2 - a} \right).\left( { - 3} \right) + \left( { - 2 - b} \right).\left( { - 6} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}30 + 6a - 4 + 2b = 0\\6 + 3a + 12 + 6b = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}6a + 2b =  - 26\\3a + 6b =  - 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 4\\b =  - 1\end{array} \right.\end{array}\)

Vậy \(H\left( { - 4; - 1} \right)\).

Chọn A.

Phương pháp giải:

- Gọi \(M\left( {x;y} \right) \in \left( P \right)\) và \(M'\left( {x';y'} \right) = F\left( M \right)\). Biểu diễn \(x\) và \(y\) theo x’ và y’.

- Thay tọa độ điểm M theo x’ và y’ vào phương trình (P), tìm ra mối liên hệ giữa x’ và y’.

- Kết luận ảnh của (P) qua phép dời hình.

Lời giải chi tiết:

Gọi \(M\left( {x;y} \right) \in \left( P \right)\) và \(M'\left( {x';y'} \right) = F\left( M \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' = x - 3\\y' = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 3\\y = y' - 1\end{array} \right.\).

\( \Rightarrow M\left( {x' + 3;y' - 1} \right)\).

Vì \(M \in \left( P \right) \Rightarrow y' - 1 = {\left( {x' + 3} \right)^2} + 1\)

\(\begin{array}{l} \Leftrightarrow y' = x{'^2} + 6x' + 9 + 1 + 1\\ \Leftrightarrow y' = x{'^2} + 6x' + 11\end{array}\)

Do đó điểm \(M'\) thuộc \(\left( {P'} \right):\,\,y = {x^2} + 6x + 11\).

Vậy phép dời hình đã cho biến \(\left( P \right):\,\,y = {x^2} + 1\) thành \(\left( {P'} \right):\,\,y = {x^2} + 6x + 11\).

Chọn C.

Phương pháp giải:

- Xác định tọa độ vectơ tịnh tiến.

- Sử dụng biểu thức tọa độ của phép tịnh tiến.

\({{T}_{\overrightarrow{v}}}\left( M \right)=M'\) với \(M\left( x;y \right);\,\,M'\left( x';y' \right);\,\,\overrightarrow{v}\left( a;b \right)\) thì \(\left\{ \begin{align}x'=x+a \\ y'=y+b \\ \end{align} \right.\).

Lời giải chi tiết:

Từ giả thiết suy ra \(\Delta '\) là ảnh của \(\Delta \) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}=\left( -2;3 \right)\).

Gọi \(M\left( {x;y} \right) \in \Delta \); 

\({T_{\overrightarrow u }}\left( M \right) = M'\left( {x';y'} \right) \Rightarrow \left\{ \begin{array}{l}
x' = x - 2\\
y' = y + 3
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
x = x' + 2\\
y = y' - 3
\end{array} \right.\)

\(\Rightarrow M\left( x'+2;y'-3 \right)\in \left( \Delta  \right)\Rightarrow \) Thay tọa độ điểm \(M\) vào phương trình \(\Delta \) ta có:

\(5\left( {x' + 2} \right) - \left( {y' - 3} \right) + 1 = 0 \Leftrightarrow 5x' - y' + 14 = 0\)

Chứng tỏ \(M'\in \left( \Delta ' \right):\,\,5x-y+14=0\).

Vậy phép tịnh tiến theo \(\overrightarrow{u}=\left( -2;3 \right)\) biến \(\Delta :\,\,5x-y+1=0\) thành đường thẳng \(\Delta ':\,\,5x - y + 14 = 0\).

Chọn A.