30 bài tập trắc nghiệm phép đối xứng trụcLàm bàiCâu hỏi 1 : Trong các chữ cái "H, A, T, R, U, N, G" có bao nhiêu chữ cái có trục đối xứng.
Đáp án: A Phương pháp giải: Lời giải chi tiết: Các từ có trục đối xứng là "H, A, T, U". Chọn A. Câu hỏi 2 : Hình nào dưới đây không có trục đối xứng?
Đáp án: D Phương pháp giải: Lời giải chi tiết:
Hình bình hành không có trục đối xứng. Chọn: D. Câu hỏi 3 : Ảnh A′ của A(4;−3) qua phép đối xứng trục d với d:2x−y=0 có tọa độ là:
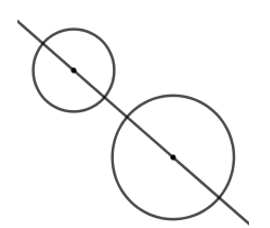
Đáp án: B Phương pháp giải: Viết phương trình đường thẳng d’ qua A và vuông góc với d. Tìm giao điểm H của d và d’. Khi đó H là trung điểm của AA’. Áp dụng công thức tìm tọa độ trung điểm {xA+xA′=2xHyA+yA′=2yH Lời giải chi tiết: Gọi A′ là ảnh của A qua phép đối xứng trục d. Gọi d’ là đường thẳng đi qua A và vuông góc với d, khi đó phương trình d’ có dạng: x + 2y + c = 0. Vì A∈d′ nên 4+2(−3)+c=0⇒c=2. Khi đó (d′):x+2y+2=0 Gọi H=d∩d′⇒H(−25;−45)⇒ H là trung điểm của AA’. Khi đó {xA′=2xH−xAyA′=2yH−yA⇒{xA′=2.(−25)−4=−245yA′=2(−45)+3=75⇒A′(−245;75) Chọn B. Câu hỏi 4 : Hình gồm 2 đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Hình gồm 2 đường tròn có tâm và bán kính khác nhau có trục đối xứng duy nhất là đường thẳng nối tâm của 2 đường tròn đó. Chọn B. Câu hỏi 5 : Trong mặt phẳng Oxy cho tam giác ABC với A(1 ; 3), B(2 ; -4), C(3 ; -2) và điểm G và trọng tâm tam giác ABC. Ảnh G’ của G qua phép đối xứng trục Ox có tọa độ là :
Đáp án: B Phương pháp giải: Áp dụng công thức tìm tọa độ trọng tâm G của tam giác ABC : {xG=xA+xB+xC3yG=yA+yB+yC3 Tìm ảnh của G qua phép đối xứng trục Ox, nếu G(a ; b) thì G’(a ; -b). Lời giải chi tiết: {xG=xA+xB+xC3=1+2+33=2yG=yA+yB+yC3=3−4−23=−1⇒G(2;−1)⇒G′(2;1) right)\) Chọn B. Câu hỏi 6 : Khẳng định nào sau đây sai ?
Đáp án: A Phương pháp giải: Phép đối xứng trục là một phép dời hình nên bảo tồn khoảng cách giữa hai điểm bất kì. Lời giải chi tiết: Phép đối xứng trục bảo toàn độ dài của vector chứ không bảo toàn phương và hướng của vector, chính vì vậy đáp án A sai. Chọn A. Câu hỏi 7 : Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 2x−y+3=0. Ảnh của đường thẳng d qua phép đối xung trục Ox có phương trình là:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Phương pháp: Lấy hai điểm bất kì thuộc d và cho đối xứng qua Ox ta được hai điểm mới. Viết phương trình đường thẳng đi qua hai điểm này ta được phương trình cần tìm. Cách giải: Xét hai điểm A(0;3),B(−32;0)∈d. Ảnh của A,B qua phép đối xứng trục Ox là A′(0;−3),B′(−32;0). →A′B′=(−32;3) nên d′ nhận →n=(2;1) làm véc tơ pháp tuyến. Phương trình d′:2(x−0)+1(y+3)=0⇔2x+y+3=0. Chọn A.
Câu hỏi 8 : Tìm m để (C):x2+y2+4x+2my+8=0 là ảnh của đường tròn (C′):(x−10)2+(y−3)2=5 qua phép đối xứng trục d, biết đường thẳng d có phương trình x=4.
Đáp án: D Phương pháp giải: Xác định tâm I và I’ của 2 đường tròn (C) và (C’). I là ảnh của I’ qua phép đối xứng trục d. Lời giải chi tiết: Đường tròn (C) có tâm I(−2;−m) là ảnh của tâm I′(10;3) của đườngtròn (C′) qua phép đối xứng trục d. II’ là đường thẳng đi qua I’ và vuông góc với d nên có phương trình y = 3. Gọi H là giao điểm của đường thẳng x = 4 và y = 3 ⇒H(4;3) là trung điểm của II’ ⇒I(−2;3) ⇔m=−3 Chọn D Câu hỏi 9 : Hình nào sau đây có nhiều trục đối xứng nhất ?
Đáp án: D Phương pháp giải: Liệt kê các trục đối xứng của từng hình. Lời giải chi tiết: Hình thoi có 2 trục đối xứng. Hình vuông có 4 trục đối xứng. Elip có 2 trục đối xứng Hình tròn có vô số trục đối xứng là các đường thẳng đi qua tâm. Chọn D. Câu hỏi 10 : Trong mặt phẳng Oxy cho parabol (P):4x2−7x+3. Phép đối xứng trục Oy biến (P) thành (P’) có phương trình:
Đáp án: B Phương pháp giải: Phép đối xứng trục Oy có: {x=−x′y=y′ Thay vào phương trình (P) để tìm phương trình (P’). Lời giải chi tiết: Phép đối xứng trục Oy có: {x=−x′y=y′ Thay vào phương trình (P) ta có: y=4(−x)2−7(−x)+3=4x2+7x+3 Chọn B. Câu hỏi 11 : Trong mặt phẳng tọa độ Oxy cho đường tròn (C’): x2+y2−10x−2y+23=0 và đường thẳng d: x – y + 2 = 0, phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục d là:
Đáp án: B Phương pháp giải: Gọi I và R là tâm và bán kính của đường tròn (C). Ảnh của (C) qua phép đối xứng trục d là đường tròn có tâm là ảnh của I qua phép đối xứng trục d và có bán kính bằng R Lời giải chi tiết: Đường tròn (C) có tâm I(5; 1), bán kính R=√25+1−23=√3. Ảnh của (C) qua phép đối xứng trục d là đường tròn có tâm là ảnh của I qua phép đối xứng trục d và có bán kính bằng √3. Gọi I’ là ảnh của I qua phép đối xứng trục d. Gọi d’ là đường thẳng đi qua I và vuông góc với d ta có phương trình d’ có dạng x + y + c = 0. I∈d′⇒5+1+c=0⇒c=−6⇒(d′):x+y−6=0 Gọi H=d∩d′⇒H(2;4) là trung điểm của II’, ta có {xI′=2xH−xIyI′=2yH−yI⇒{xI′=2.2−5=−1yI′=2.4−1=7⇒I′(−1;7) Vậy phương trình đường tròn (C’) là (x+1)2+(y−7)2=3⇔x2+y2+2x−14y+47=0 Chọn B. Câu hỏi 12 : Trong mặt phẳng Oxy, cho hai đường tròn (C):(x−1)2+(y−2)2=4 và (C′):(x−3)2+y2=4. Viết phương trình trục đối xứng của (C) và (C′)
Đáp án: B Phương pháp giải: Xác định tâm I và I’ của đường tròn (C) và (C’). Trục đối xứng của 2 đường tròn (C) và (C’) là đường thẳng đi qua H và nhận →II′ là 1 VTPT. Lời giải chi tiết: Đường tròn (C) có tâm I(1;2), đường tròn (C′) có tâm I′(3;0) Gọi H là trung điểm của II’ ta có H(2;1) Trục đối xứng của 2 đường tròn (C) và (C’) là đường thẳng đi qua H và nhận →II′=(2;−2)=2(1;−1) là 1 VTPT ⇒ Trục đối xứng của 2 đường tròn (C) và (C’) có phương trình 1(x−2)−1(y−1)=0⇔x−2−y+1=0⇔y=x−1 Chọn B. Câu hỏi 13 : Khẳng định nào sau đây sai ?
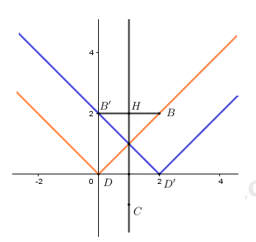
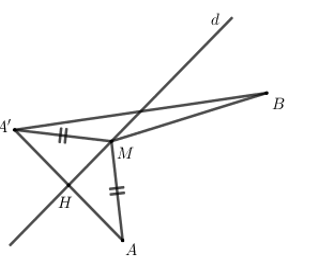
Đáp án: A Phương pháp giải: Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì. Lời giải chi tiết: Phép đối xứng trục không bào toàn hướng của vector. Chọn A. Câu hỏi 14 : Trong mặt phẳng Oxy cho đường thẳng d có phương trình x−y+1=0 và hai điểmA(3;1);B(7;5). Tìm điểm M thuộc d sao cho MA+MB nhỏ nhất ?
Đáp án: C Phương pháp giải: Gọi A’ là điểm đối xứng với A qua d, ta có : MA=MA′ Áp dụng BĐT tam giác ta có ⇒MA+MB=MA′+MB≥A′B⇒(MA+MB)min thẳng hàng. Lời giải chi tiết: Ta dễ dàng kiểm tra được A, B nằm cùng phía so với đường thẳng d. Gọi A’ là điểm đối xứng với A qua d, ta có : MA=MA’ \Rightarrow MA+MB=MA'+MB\ge A'B \Rightarrow MA+MB nhỏ nhất \Leftrightarrow M,A',B thẳng hàng hay M=A'B\cap d. Đường thẳng AA’ đi qua A và vuông góc với d nên có phương trình x+y-4=0\,\,\left( d' \right). Gọi H=d\cap d'\Rightarrow Tọa độ điểm H là nghiệm của hệ \left\{ \begin{array}{l}x - y + 1 = 0\\x + y - 4 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \frac{3}{2}\\y = \frac{5}{2}\end{array} \right. \Rightarrow H\left( {\frac{3}{2};\frac{5}{2}} \right) là trung điểm của AA’ \Rightarrow \left\{ \begin{align} {{x}_{A'}}=2{{x}_{H}}-{{x}_{A}}=0 \\ {{y}_{A'}}=2{{y}_{H}}-{{y}_{H}}=4 \\ \end{align} \right.\Rightarrow A'\left( 0;4 \right) \Rightarrow Phương trình đường thẳng A’B là : \frac{x-0}{7-0}=\frac{y-4}{5-4}\Leftrightarrow \frac{x}{7}=y-4\Leftrightarrow x-7y+28=0 \Rightarrow MA+MB nhỏ nhất \Leftrightarrow M=A'B\cap d\Rightarrow Tọa độ điểm M là nghiệm của hệ \left\{ \begin{array}{l}x - y + 1 = 0\\x - 7y + 28 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{7}{2}\\y = \frac{9}{2}\end{array} \right. \Rightarrow M\left( {\frac{7}{2};\frac{9}{2}} \right) Chọn C. Câu hỏi 15 : Cho hàm số \left( C \right):\,\,y=\left| x \right| Giả sử \left( C' \right) đối xứng với \left( C \right) qua đường thẳng x=1. Khi đó, đồ thị \left( C' \right) có dạng :
Đáp án: D Phương pháp giải: \left( C \right):\,\,y=\left| x \right|=\left[ \begin{align} x\,\,khi\,\,x\ge 0\,\,\,\,\,\,\left( {{d}_{1}} \right) \\ -x\,\,khi\,\,x<0\,\,\,\left( {{d}_{2}} \right) \\ \end{align} \right. Tìm ảnh của {{d}_{1}} và {{d}_{2}} qua phép đối xứng qua trục la đường thẳng x = 1. Lời giải chi tiết:
\left( C \right):\,\,y=\left| x \right|=\left[ \begin{align} x\,\,khi\,\,x\ge 0\,\,\,\,\,\,\left( {{d}_{1}} \right) \\ -x\,\,khi\,\,x<0\,\,\,\left( {{d}_{2}} \right) \\ \end{align} \right. {{d}_{1}}\cap \left( x=1 \right)=A\left( 1;1 \right) Lấy B\left( 2;2 \right)\in {{d}_{1}}\Rightarrow đường thẳng đi qua B và vuông góc với \left( x=1 \right) có phương trình y = 2. Gọi H là giao điểm của đường thẳng x = 1 và y = 2 \Rightarrow H\left( 1;2 \right) Gọi B’ là điểm đối xứng với B qua đường thẳng x = 1 \Rightarrow H là trung điểm của BB’ \Rightarrow B'\left( 0;2 \right) \Rightarrow Phương trình đường thẳng AB’ là \frac{x-1}{0-1}=\frac{y-1}{2-1}\Leftrightarrow -x+1=y-1\Leftrightarrow x+y=2 \Rightarrow x+y=2 là đường thẳng đối xứng với đường thẳng y = x qua đường thẳng x = 1. {{d}_{2}}\cap \left( x=1 \right)=C\left( 1;-1 \right) Lấy D\left( 0;0 \right)\in {{d}_{2}}\Rightarrow Đường thẳng đi qua D và vuông góc với đường thẳng x = 1 có phương trình y = 0. Gọi K là giao điểm của đường thẳng x = 1 và y = 0 \Rightarrow K\left( 1;0 \right) Gọi D’ là điểm đối xứng với D qua đường thẳng x = 1 \Rightarrow K là trung điểm của DD’ \Rightarrow D'\left( 2;0 \right) \Rightarrow Phương trình đường thẳng CD’ là : \frac{x-1}{2-1}=\frac{y+1}{0+1}\Leftrightarrow x-1=y+1\Leftrightarrow x-y=2 \Rightarrow x-y=2 là đường thẳng đối xứng với đường thẳng y=-x qua đường thẳng x=1
\Rightarrow \left( {C'} \right):\,\,\left[ \begin{array}{l}x + y = 2\\x - y = 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}y = - x + 2\\y = x - 2\end{array} \right. \Leftrightarrow y = \left| {x - 2} \right| Chọn D. Câu hỏi 16 : Trên tia phân giác ngoài Cx của góc C của tam giác ABC lấy điểm M không trùng với C. Tìm mệnh đề đúng nhất ?
Đáp án: A Phương pháp giải: Lấy A ‘đối xứng với A qua Cx. Lời giải chi tiết:
Lấy A’ đối xứng với A qua Cx ta có : \begin{array}{l}\left\{ \begin{array}{l}MA = MA'\\CA = CA'\end{array} \right.\\ \Rightarrow MA + MB = MA' + MB > A'B = CA' + CB = CA + CB\end{array} Chọn A. Câu hỏi 17 : Cho điểm A\left( 2;1 \right). Tìm điểm B trên trục hoành và điểm C trên đường phân giác của góc phần tư thứ nhất để chu vi tam giác ABC nhỏ nhất.
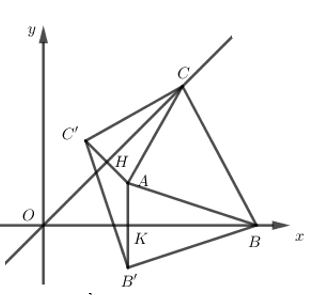
Đáp án: B Phương pháp giải: Gọi B’, C’ lần lượt là điểm đối xứng với A qua trục Ox và đường thẳng y = x ta có : AB=BB',AC=CC’ \begin{align} C=AB+BC+CA=B'B+BC+CC'\ge B'C' \\ \Rightarrow {{C}_{\min }}=B'C'\Leftrightarrow B=Ox\cap B'C',\,\,C=\left( y=x \right)\cap B'C' \\ \end{align} Lời giải chi tiết:
Gọi B’, C’ lần lượt là điểm đối xứng với A qua trục Ox và đường thẳng y = x ta có : AB=BB',AC=CC’ Dễ thấy B'\left( 2;-1 \right) AC’ là đường thẳng đi qua A và vuông góc với đường thẳng y = x nên có phương trình x + y – 3 = 0. Gọi H là giao điểm của đường thẳng y = x và x + y – 3 = 0 \Rightarrow H\left( \frac{3}{2};\frac{3}{2} \right) là trung điểm của AC’ \Rightarrow C'\left( 1;2 \right) Chu vi tam giác ABC \begin{align} C=AB+BC+CA=B'B+BC+CC'\ge B'C' \\ \Rightarrow {{C}_{\min }}=B'C'\Leftrightarrow B=Ox\cap B'C',\,\,C=\left( y=x \right)\cap B'C' \\ \end{align} Phương trình B’C’ : \frac{x-2}{1-2}=\frac{y+1}{2+1}\Leftrightarrow -x+2=\frac{y+1}{3}\Leftrightarrow -3x+6=y+1\Leftrightarrow 3x+y-5=0 \Rightarrow B\left( \frac{5}{3};0 \right),C\left( \frac{5}{4};\frac{5}{4} \right) Chọn B. Câu hỏi 18 : Cho x, y thỏa mãn x-2y+2=0. Tìm giá trị nhỏ nhất của biểu thức T=\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-5 \right)}^{2}}}+\sqrt{{{\left( x-5 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}
Đáp án: A Phương pháp giải: Gọi M\left( x;y \right) thỏa mãn x-2y+2=0\Rightarrow M thuộc đường thẳng x-2y+2=0\,\,\left( d \right). Gọi A\left( 3;5 \right);B\left( 5;7 \right)\Rightarrow T=MA+MB Đưa về bài toán tìm điểm M\in d sao cho MA+MB nhỏ nhất. Lời giải chi tiết:
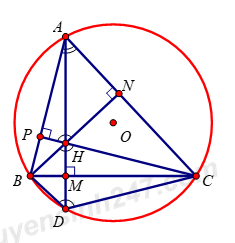
Gọi M\left( x;y \right) thỏa mãn x-2y+2=0\Rightarrow M thuộc đường thẳng x-2y+2=0\,\,\left( d \right). Gọi A\left( 3;5 \right);B\left( 5;7 \right)\Rightarrow T=MA+MB Ta cần tìm điểm M\in d sao cho MA+MB nhỏ nhất. Dễ thấy A, B nằm cùng phía so với đường thẳng d. Gọi A’ là điểm đối xứng với A qua d, ta có : MA=MA’ \Rightarrow MA+MB=MA'+MB\ge A'B \Rightarrow MA+MB nhỏ nhất \Leftrightarrow M,A',B thẳng hàng hay M=A'B\cap d. Đường thẳng AA’ đi qua A và vuông góc với d nên có phương trình 2x+y-11=0\,\,\left( d' \right). Gọi H=d\cap d'\Rightarrow Tọa độ điểm H là nghiệm của hệ \left\{ \begin{array}{l}x - 2y + 2 = 0\\2x + y - 11 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right. \Rightarrow H\left( {4;3} \right) \Rightarrow Phương trình đường thẳng A’B là : x = 5. \Rightarrow MA+MB nhỏ nhất \Leftrightarrow M=A'B\cap d\Rightarrow Tọa độ điểm M là nghiệm của hệ \left\{ \begin{array}{l}x - 2y + 2 = 0\\x = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = \frac{7}{2}\end{array} \right. \Rightarrow M\left( {5;\frac{7}{2}} \right) \Rightarrow {T_{\min }} = 6 Chọn A. Câu hỏi 19 : Cho hai điểm B và C cố định trên đường tròn \left( O;R \right). Điểm A thay đổi trên \left( O;R \right). Gọi H là trực tâm của \Delta ABC và D là điểm đối xứng của H qua đường thẳng BC. Mệnh đề nào sau đây là đúng?
Đáp án: D Phương pháp giải: Vẽ hình và dựa vào các kiên thức về tứ giác nội tiếp. Lời giải chi tiết:
Trong một tam giác, điểm đối xứng của trực tâm H qua một cạnh của nó thì nằm trên đường tròn ngoại tiếp tam giác đó. Đây là một kiến thức cơ bản. Tuy nhiên ta có thể chứng minh lại bài toán này như sau: Kẻ các đường cao AM, BN, CP và gọi D là điểm đối xứng của H qua BC. Ta có tứ giác ANHP là một tứ giác nội tiếp, suy ra: \widehat{PAN}+\widehat{PHN}={{180}^{o}} hay \widehat{BAC}+\widehat{BHC}={{180}^{o}}. Mặt khác, có D là điểm đối xứng của H qua BC nên \widehat{BDC}=\widehat{BHC}. Do đó: \widehat{BAC}+\widehat{BDC}={{180}^{o}}. Suy ra D nằm trên đường tròn (O) ngoại tiếp \Delta ABC. Chọn D. Câu hỏi 20 : Cho M\left( {2;3} \right). Hỏi điểm nào trong các điểm sau là ảnh của M qua phép đối xứng trục Ox?
Đáp án: A Phương pháp giải: Điểm M'\left( {x; - y} \right) là ảnh của điểm M\left( {x;y} \right) qua phép đối xứng trục Ox. Lời giải chi tiết: Điểm Q\left( {2; - 3} \right) là ảnh của điểm M\left( {2;3} \right) qua phép đối xứng trục Ox. Chọn A. Câu hỏi 21 : Cho đường thẳng \Delta :\ x+y-2=0 Đường thẳng \Delta ' đối xứng với \Delta qua trục hoành có phương trình:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Gọi A\left( {{x}_{0}};\ 0 \right) là giao điểm của \Delta và Ox\Rightarrow A\left( 2;\ 0 \right). Đường thẳng \Delta ' đối xứng với \Delta qua trục hoành \Rightarrow A\in \Delta ' Phương trình đường thẳng \Delta ' đi qua A và có hệ số góc k là: y=k\left( x-2 \right)\Leftrightarrow kx-y-2k=0 Gọi B\left( 1;\ 1 \right)\in \Delta \Rightarrow B'\left( 1;-k \right)\in \Delta ' là điểm đối xứng với B qua Ox \Rightarrow d\left( {B;\;Ox} \right) = d\left( {B';\;Ox} \right) \Leftrightarrow \left| k \right| = 1 \Leftrightarrow \left[ \begin{array}{l} k = - 1 \Rightarrow \Delta ':\;\; - x - y + 2 = 0 \Leftrightarrow x + y - 2 = 0\;\;\;\left( {ktm} \right)\\ k = 1 \Rightarrow \Delta ':\;x - y - 2 = 0\;\;\left( {tm} \right)\; \end{array} \right. Chọn B. Câu hỏi 22 : Hình nào trong các hình sau không có trục đối xứng?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Hình bình hành không có trục đối xứng. Hình tam giác đều có 3 trục đối xứng. Hình thoi có 2 trục đối xứng. Hình vuông có 4 trục đối xứng. Chọn: D Câu hỏi 23 : Trong mặt phẳng tọa độ Oxy, tìm ảnh của đường tròn \left( C \right):\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4 qua phép đối xứng trục Ox.
Đáp án: C Phương pháp giải: Phép đối xứng trục Ox biến M\left( {x;y} \right) thành M'\left( {x; - y} \right); biến đường tròn \left( {I\left( {a;b} \right);\,R} \right)thành đường tròn \left( {I'\left( {a; - b} \right);\,R} \right). Lời giải chi tiết: Ảnh của đường tròn \left( C \right):\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4 có tâm I\left( {1; - 2} \right) bán kính R = 2 qua phép đối xứng trục Ox là: \left( C \right):\,{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4 có tâm I'\left( {1;2} \right) bán kính R = 2. Chọn: C Câu hỏi 24 : Trong mặt phẳng tọa độ Oxy, cho đường tròn \left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9. Viết phương trình đường tròn \left( {C'} \right) là ảnh của đường tròn \left( C \right) qua phép đối xứng trục Oy.
Đáp án: A Phương pháp giải: {_{Oy}}:\,\,\,M\left( {x;y} \right)\, \mapsto M'\,\left( {x';y'} \right)\, \Leftrightarrow \left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right. . Lời giải chi tiết: Đường tròn \left( C \right):{{\left( x-2 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=9 có tâm I\left( 2;-3 \right), bán kính R=3
Phép đối xứng trục biến đường tròn thành đường tròn có cùng bán kính \Rightarrow R'=3 Đồng thời, biến tâm I\left( 2;-3 \right) thành tâm I'\left( -2;-3 \right) Phương trình đường tròn \left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 9. Chọn: A Câu hỏi 25 : Cho hai đường thẳng \left( \Delta \right):\,\,x - y + 1 = 0;\,\,\left( {\Delta '} \right):\,\,x - y - 5 = 0. Có bao nhiêu đường thẳng (d) thoả mãn điều kiện phép đối xứng trục (d) biến \left( \Delta \right) thành \left( {\Delta '} \right)?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Có duy nhất 1 đường thẳng (d) thỏa mãn điều kiện phép đối xứng trục (d) biến \left( \Delta \right) thành \left( {\Delta '} \right) là \left( d \right):\,\,x - y - 2 = 0. Chọn B. Câu hỏi 26 : Cho hai điểm A\left( {1;2} \right);\,\,A'\left( {3;4} \right). Nếu A' = {D_\Delta }\left( A \right) thì đường thẳng \left( \Delta \right) có phương trình là
Đáp án: C Phương pháp giải: +) Do A’ đối xứng A qua \left( \Delta \right) nên đường thẳng \left( \Delta \right) là đường trung trực của AA’. Từ đó xác định điểm đi qua và 1VTPT của đường thẳng \left( \Delta \right). +) Đường thẳng đi qua M\left( {{x_0};{y_0}} \right) và có 1 VTPT \overrightarrow n = \left( {a;b} \right) có phương trình a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0. Lời giải chi tiết: Do A’ đối xứng A qua \left( \Delta \right) nên đường thẳng \left( \Delta \right) là đường trung trực của AA’. Do đó \left( \Delta \right) đi qua trung điểm I\left( {2;3} \right) của AA’ và nhận \overrightarrow {AA'} = \left( {2;2} \right) là 1 VTPT. Khi đó ta có phương trình \left( \Delta \right):\,\,2\left( {x - 2} \right) + 2\left( {y - 3} \right) = 0 \Leftrightarrow x + y - 5 = 0. Chọn C. Câu hỏi 27 : Cho hình vuông ABCD có hai đường chéo AC và BD cắt nhau tại I. Khẳng định nào sau đây là đúng về phép đối xứng trục:
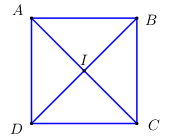
Đáp án: C Phương pháp giải: Sử dụng định nghĩa phép đối xứng trục. Lời giải chi tiết:
Do ABCD nên hai đường chéo AC \bot BD và AC \cap BD tại trung điểm của mỗi đường. \Rightarrow AC là trung trực của BD \Rightarrow Đ_{AC}\left( D \right) = B. Chọn C Câu hỏi 28 : Tìm mệnh đề sai trong các mệnh đề sau:
Đáp án: B Phương pháp giải: Sử dụng định nghĩa phép đối xứng trục. Lời giải chi tiết: Khẳng định sai là B. Phép đối xứng trục biến đường thẳng thành đường thẳng chứ không nhất thiết song song hoặc trùng với đường thẳng đã cho. Chọn B Câu hỏi 29 : Trong mặt phẳng Oxy , cho điểm M\left( {2;3} \right). Hỏi trong bốn điểm sau điểm nào là ảnh của M qua phép đối xứng qua đường thẳng d:\,\,x - y = 0?
Đáp án: A Phương pháp giải: Đ_{Ox}\left[ {M\left( {x;y} \right)} \right] = M'\left( {x';y'} \right) \Rightarrow \left\{ \begin{array}{l}x' = x\\y' = - y\end{array} \right. Lời giải chi tiết: Cách 1: Gọi Đ_\Delta \left( M \right) = M'. Bước 1: Dựng phương trình đường thẳng d' qua M và vuông góc với d. \Rightarrow d':\,\,x + y + c = 0. Thay M:\,\,2 + 3 + c = 0 \Leftrightarrow c = - 5 \Rightarrow t:\,\,x + y - 5 = 0. Bước 2: Gọi H là hình chiếu vuông góc của M trên d \Rightarrow H = d \cap d'. \Rightarrow H\,\,\left\{ \begin{array}{l}x - y = 0\\x + y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = \frac{5}{2}\end{array} \right. \Rightarrow H\left( {\frac{5}{2};\frac{5}{2}} \right). Bước 3: Do M, M’ đối xứng nhau qua d \Rightarrow H là trung điểm của MM’ \Leftrightarrow M'\,\,\left\{ \begin{array}{l}x' = 2{x_H} - {x_M}\\y' = 2{y_H} - {y_M}\end{array} \right. \Rightarrow M'\,\,\left\{ \begin{array}{l}x' = 2.\frac{5}{2} - 2 = 3\\y' = 2.\frac{5}{2} - 3 = 2\end{array} \right. \Rightarrow M'\left( {3;2} \right). Cách 2: Công thức giải nhanh: M' = M - 2nT T = \frac{{x - y}}{{{1^2} + {{\left( { - 1} \right)}^2}}} = \frac{{2 - 3}}{2} = \frac{{ - 1}}{2} \Rightarrow M'\,\,\left\{ \begin{array}{l}x' = 2 - 2.1.\frac{{ - 1}}{2} = 3\\y' = 3 - 2.\left( { - 1} \right).\frac{{ - 1}}{2} = 2\end{array} \right. \Rightarrow M'\left( {3;2} \right). Chọn A Câu hỏi 30 : Cho đường tròn \left( C \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 4. Tìm ảnh của (C) qua phép đối xứng trục d:\,\,x + y - 2 = 0.
Đáp án: D Phương pháp giải: - Xác định tâm I và bán kính R của đường tròn \left( C \right). - \left( {C'} \right) = Đ_d\left( C \right) \Rightarrow \left( {C'} \right) là đường tròn có tâm I' = Đ_d\left( I \right) và bán kính R' = R. Lời giải chi tiết: Đường tròn \left( C \right) có tâm I\left( {1; - 1} \right) và bán kính R = 2. Gọi \left( {C'} \right) = Đ_d\left( C \right) \Rightarrow \left( {C'} \right) là đường tròn có tâm I' = Đ_d\left( I \right) và bán kính R = 2. Tìm I' = Đ_d\left( I \right). Cách 1: Gọi I' = Đ_d\left( I \right). Bước 1: Dựng phương trình đường thẳng d' qua I và vuông góc với d. \Rightarrow d':\,\,x - y + c = 0. Thay I:\,\,1 - \left( { - 1} \right) + c = 0 \Leftrightarrow c = - 2 \Rightarrow t:\,\,x - y - 2 = 0. Bước 2: Gọi H là hình chiếu vuông góc của I trên d \Rightarrow H = d \cap d'. \Rightarrow H\,\,\left\{ \begin{array}{l}x + y - 2 = 0\\x - y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \Rightarrow H\left( {2;0} \right). Bước 3: Do I, I’ đối xứng nhau qua d \Rightarrow H là trung điểm của II’ \Leftrightarrow I'\,\,\left\{ \begin{array}{l}x' = 2{x_H} - {x_I}\\y' = 2{y_H} - {y_I}\end{array} \right. \Rightarrow I'\,\,\left\{ \begin{array}{l}x' = 2.2 - 1 = 3\\y' = 2.0 - \left( { - 1} \right) = 1\end{array} \right. \Rightarrow I'\left( {3;1} \right). Cách 2: Công thức giải nhanh: I' = I - 2nT T = \dfrac{{x + y - 2}}{{{1^2} + {1^2}}} = \dfrac{{1 + \left( { - 1} \right) - 2}}{2} = - 1 \Rightarrow I'\,\,\left\{ \begin{array}{l}x' = 1 - 2.1.\left( { - 1} \right) = 3\\y' = - 1 - 2.1.\left( { - 1} \right) = 1\end{array} \right. \Rightarrow I'\left( {3;1} \right). Vậy phương trình \left( {C'} \right):\,\,\left( {C'} \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4. Chọn D. |