Phương pháp giải:

Phương pháp:

M và M’ đối xứng qua I nên I là trung điểm của MM’.

Lời giải chi tiết:

Cách giải:

M và M’ đối xứng qua I nên I là trung điểm của MM’.

Ta có: 

\(\left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M}\\{y_{M'}} = 2{y_I} - {y_M}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = 4\\{y_{M'}} = - 5\end{array} \right. \Rightarrow M'\left( {4; - 5} \right)\)

Chọn C.

Phương pháp giải:

Gọi M’ là điểm đối xứng với M qua tâm I \(\Rightarrow I\) là trung điểm của MM’.

Lời giải chi tiết:

Gọi M’ là điểm đối xứng với M qua tâm I \(\Rightarrow I\) là trung điểm của MM’.

\(\Rightarrow \left\{ \begin{align}  {{x}_{M'}}=2{{x}_{I}}-{{x}_{M}}=-1 \\  {{y}_{M'}}=2{{y}_{I}}-{{y}_{M}}=5 \\ \end{align} \right.\Rightarrow M'\left( -1;5 \right)\)

Chọn B.

Phương pháp giải:

Đ\(_{I}\left( M \right)=\,M'\Rightarrow I\) là trung điểm của MM’

Lời giải chi tiết:

 Đ\(_{I}\left( I \right)\,=\,I\Rightarrow \) Phép đối xứng tâm có đúng một điểm biến thành chính nó. Điểm đó chính là tâm đối xứng.

Chọn B.

Phương pháp giải:

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song với nó.

Lời giải chi tiết:

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song với nó.

Dựa vào các đáp án ta thấy chỉ có đường thẳng đáp án C song song với đường thẳng d đã cho.

Chọn C.

Phương pháp giải:

Đ\(_{I}\left( M \right)\,=M'\Rightarrow I\) là trung điểm của MM’

Lời giải chi tiết:

Đ\(_{I}\left( M \right)=M'\Rightarrow I\) là trung điểm của MM’

\( \Rightarrow \left\{ \begin{array}{l}x + x' = 2a\\y + y' = 2b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = 2a - x\\y' = 2b - y\end{array} \right.\)

Chọn B.

Phương pháp giải:

Hình có tâm đối xứng nếu và chỉ nếu tồn tại phép đối xứng tâm biến hình (H) thành chính nó.

Lời giải chi tiết:

Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.

Hình tròn có tâm đối xứng là tâm của nó.

Hình thoi có tâm đối xứng là giao điểm của hai đường chéo.

Tam giác đều không có tâm đối xứng.

Chọn C.

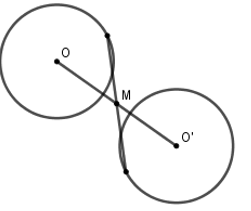
Phương pháp giải:

Sử dụng các tính chất của phép đối xứng tâm.

Lời giải chi tiết:

Dễ thấy các đáp án A, C, D đúng, chỉ có đáp án B sai.

Đ\(_{I}\left( M \right)\,=\,M'\Rightarrow I\) là trung điểm của MM’ \(\Rightarrow IM'=IM\) và ba điểm I, M, M’ thẳng hàng.

Chọn B.

Phương pháp giải:

Vẽ hình và tìm tâm đối xứng.

Lời giải chi tiết:

Hình gồm hai đường tròn phân biệt có cùng bán kính có tâm đối xứng duy nhất là trung điểm có đoạn thẳng nối tâm hai đường tròn đó.

Chọn B.

Phương pháp giải:

Phép đối xứng tâm biến đường tròn thành đường tròn khác cùng bán kính.

Lời giải chi tiết:

Đường tròn (C) có tâm \(K\left( 0;0 \right)\) và bán kính \(R=1\)

Gọi Đ\(_{I}\left( K \right)\,=K'\Rightarrow \) I là trung điểm của KK’ \(\Rightarrow K'\left( 2;0 \right)\)

Đ\(_{I}\left( C \right)\,=\left( C' \right)\Rightarrow \) Đường tròn (C’) có tâm \(K'\left( 2;0 \right)\) và bán kính \(R'=R=1\)

Vậy phương trình đường tròn (C’) là: \({{\left( x-2 \right)}^{2}}+{{y}^{2}}=1\)

Chọn A.

Phương pháp giải:

Phép đối xứng tâm biến đường tròn thành đường tròn khác cùng bán kính.

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(K\left( 1;3 \right)\) và có bán kính \(R=4\)

Đ\(_{I}\left( A \right)\,=\,B,\) Đ\(_{I}\left( C \right)\,=\left( C' \right)\Rightarrow B\left( a;b \right)\) là tâm của đường tròn \(\left( C' \right)\)  và đường tròn \(\left( C' \right)\) có bán kính \(R'=R=4\). Vậy phương trình đường tròn \(\left( C' \right)\) là: \({{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}=16\)

Chọn D.

Phương pháp giải:

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Lời giải chi tiết:

Gọi d’ là ảnh của đường thẳng d qua phép đối xứng tâm I \(\Rightarrow d'//d\Rightarrow \) phương trình d’ có dạng \(x+y+c=0\)

Lấy \(A\left( -1;-1 \right)\in d\). Gọi A’ là ảnh của A qua phép đối xứng tâm I \(\Rightarrow I\) là trung điểm của AA’ \(\Rightarrow A'\left( 3;3 \right)\)

\(\Rightarrow A'\in d'\Leftrightarrow 3+3+c=0\Leftrightarrow c=-6\)

Vậy phương trình đường thẳng d’ là \(x+y-6=0\)

Chọn C.

Phương pháp giải:

Đ\(_{I}\left( M \right)\,=M'\Rightarrow I\) là trung điểm của MM’

Lời giải chi tiết:

Đ\(_{I}\left( A \right)\,=A'\Rightarrow I\) là trung điểm của AA’ \(\Rightarrow I\left( 1;3 \right)\)

Đ\(_{I}\left( B \right)\,=B'\Rightarrow I\) là trung điểm của BB’ \(\Rightarrow B\left( 1;7 \right)\)

Chọn A.

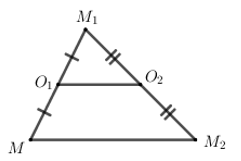
Phương pháp giải:

Nếu phép đối xứng tâm biến a thành b thì tâm đối xứng nằm trên đường thẳng song song và cách đều a và b

Lời giải chi tiết:

Nếu phép đối xứng tâm biến a thành b thì tâm đối xứng nằm trên đường thẳng song song và cách đều a và b.

Đường thẳng song song và cách đều a và b có phương trình là \(3x+4y+2=0\)

Ta thấy chỉ có điểm \(I\left( 2;-2 \right)\) thuộc đường thẳng \(3x+4y+2=0\).

Chọn A.

Phương pháp giải:

Đ\(_{{{O}_{1}}}\left( M \right)={{M}_{1}}\Rightarrow {{O}_{1}}\) là trung điểm của \(M{{M}_{1}}\)

Đ\(_{{{O}_{2}}}\left( {{M}_{1}} \right)={{M}_{2}}\Rightarrow {{O}_{2}}\) là trung điểm của \({{M}_{1}}{{M}_{2}}\)

Lời giải chi tiết:

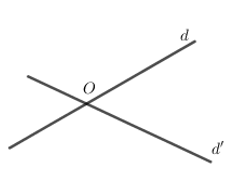
Đ\(_{{{O}_{1}}}\left( M \right)={{M}_{1}}\Rightarrow {{O}_{1}}\) là trung điểm của \(M{{M}_{1}}\)

Đ\(_{{{O}_{2}}}\left( {{M}_{1}} \right)={{M}_{2}}\Rightarrow {{O}_{2}}\) là trung điểm của \({{M}_{1}}{{M}_{2}}\)

\(\Rightarrow {{O}_{1}}{{O}_{2}}\) là đường trung bình của tam giác \(M{{M}_{1}}{{M}_{2}}\)

\(\Rightarrow {{O}_{1}}{{O}_{2}}//M{{M}_{2}}\) và \(2{{O}_{1}}{{O}_{2}}=M{{M}_{2}}\)

 \(\Rightarrow \overrightarrow{M{{M}_{2}}}=2\overrightarrow{{{O}_{1}}{{O}_{2}}}\)

Chọn A.

Phương pháp giải:

Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.

Lời giải chi tiết:

Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.

Gọi O là tâm đối xứng sao cho qua phép đối xứng tâm O biến mỗi đường thẳng d và d’ thành chính nó.

\(\Rightarrow \left\{ \begin{align}  O\in d \\  O\in d' \\ \end{align} \right.\Rightarrow O=d\cap d'\) và O là duy nhất.

Chọn B.

Phương pháp giải:

Đồ thị của một hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.

Lời giải chi tiết:

Giả sử đồ thị hàm số \(y=f\left( x \right)\) nhận gốc tọa độ O làm tâm đối xứng. Điểm \(M\left( x;y \right)\) thuộc đồ thị hàm số \(y=f\left( x \right)\Rightarrow M'\left( -x;-y \right)\) là điểm đối xứng với M qua gốc tọa độ O cũng thuộc đồ thị hàm số  \(y=f\left( x \right)\)

\(\Rightarrow -y=f\left( -x \right)\Rightarrow f\left( -x \right)=-f\left( x \right)\Rightarrow y=f\left( x \right)\) là hàm số lẻ.

Vậy hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.

Dựa vào các đáp án ta thấy đáp án D có : \(f\left( -x \right)=\sin \left( -x \right)\sqrt{{{\left( -x \right)}^{2}}+1}=-\sin x\sqrt{{{x}^{2}}+1}=-f\left( x \right)\)

\(\Rightarrow \) Hàm số \(y=\sin x\sqrt{{{x}^{2}}+1}\) là hàm số lẻ và nhận gốc tọa độ O là tâm đối xứng.

Chọn D.

Phương pháp giải:

Sử dụng biểu thức tọa độ.

Lời giải chi tiết:

Lấy điểm 

\(\left\{ \begin{array}{l}x' =  - 6 - x\\y' = 2 - y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x =  - 6 - x'\\y = 2 - y'\end{array} \right. \Rightarrow M\left( { - 6 - x';2 - y'} \right) \in \left( P \right)\)

Thay vào ta có :

\(\begin{align}  2-y'={{\left( -6-x' \right)}^{2}}-2\left( -6-x' \right) \\  \Leftrightarrow 2-y'=x{{'}^{2}}+12x'+36+12+2x' \\  \Leftrightarrow y'=-x{{'}^{2}}-14x'-46 \\ \end{align}\) 

Do Đ\(_{I}\left( P \right)=\left( P' \right)\Rightarrow M'\in \left( P' \right)\), do đó phương trình parabol (P’) là: \(y=-{{x}^{2}}-14x-46\)

Chọn A.

Phương pháp giải:

Lấy điểm \(M\left( x;y \right)\) bất kì thuộc \(\Delta \Rightarrow \) Tọa độ điểm \(M'\) là ảnh của M qua phép đối xứng tâm I.

Từ đó suy ra phương trình đường thẳng \(\Delta '\)

Lời giải chi tiết:

Lấy điểm \(M\left( x;y \right)\in \Delta \), gọi \(\left\{ \begin{array}{l}x + x' = 2a\\y + y' = 2b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2a - x'\\y = 2b - y'\end{array} \right.\) 

Thay vào phương trình \(\Delta \) ta có:

\(\begin{align}  A\left( 2a-x' \right)+B\left( 2b-y' \right)+C=0 \\  \Leftrightarrow 2aA-Ax'+2bB-By'+C=0 \\  \Leftrightarrow Ax'+By'-C-2aA-2bB=0 \\ \end{align}\)

Do \(M'\left( x';y' \right)\in \Delta '\), do đó phương trình đường thẳng \(\Delta '\) có dạng:  \(\left( \Delta ' \right):\,\,Ax+By-C-2aA-2bB=0\)

Chọn D.

Phương pháp giải:

Suy luận từng đáp án.

Lời giải chi tiết:

(I) đúng, tâm đối xứng của hình đó chính là giao điểm của hai trục đối xứng.

(II) Cách dựng đường thẳng d’ là ảnh của d qua phép đối xứng tâm O.

Bước 1: Lấy một điểm M bất kì thuộc d

Bước 2: Vẽ đường tròn tâm O bán kính OM.

Bước 3: Kéo dài OM, cắt đường tròn tâm O bán kính OM tại điểm thứ hai N.

Bước 4: Qua N kẻ đường thẳng song song với d.

Vậy ta cần dùng compa ở bước 2 và dùng thước ở bước 3 và 4.

Do đó cả (I) và (II) đều đúng.

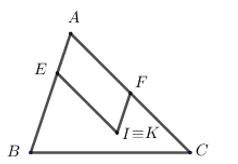
Chọn C.

Phương pháp giải:

Lấy điểm \(M\left( x;y \right)\) bất kì thuộc P, suy ra tọa độ điểm M’(x’; y’) là ảnh của M qua phép đối xứng tâm A và tọa độ điểm M’’(x’’; y’’) là ảnh của M’ qua phép đối xứng tâm B.

Lập phương trình biểu diễn mối quan hệ giữa x’’ và y’’, từ đó suy ra phương trình (P’’).

Lời giải chi tiết:

Gọi \(M\left( x;y \right)\) là điểm bất kì thuộc (P). Gọi \(M'\left( x';y' \right)\) là ảnh của M qua phép đối xứng tâm A \(\Rightarrow A\) là trung điểm của MM’, do đó ta có : \(\left\{ \begin{align}  x=-x' \\  y=2-y' \\ \end{align} \right.\,\,\left( 1 \right)\)

Gọi \(M''\left( x'';y'' \right)\) là ảnh của điểm M’ qua phép đối xứng tâm B \(\Rightarrow B\) là trung điểm của M’M’’, do đó ta có:

\(\left\{ \begin{align}  x'=4-x'' \\  y'=-2-y'' \\ \end{align} \right.\,\,\,\left( 2 \right)\) , thay vào (1) ta có: \(\left\{ \begin{align}  x=-4+x'' \\  y=4+y'' \\ \end{align} \right.\Rightarrow M\left( -4+x'';4+y'' \right)\)

Do điểm \(M\in \left( P \right)\Rightarrow \) Thay tọa độ điểm M vào phương trình parabol (P) ta có:

\(\begin{align}  4+y''={{\left( -4+x'' \right)}^{2}}\Leftrightarrow 4+y''=x'{{'}^{2}}-8x''+16 \\  \Leftrightarrow y''=x'{{'}^{2}}-8x''+12 \\ \end{align}\)

\(\begin{align}  \left( P \right)\,\xrightarrow{{{Đ}_{A}}}\,\left( P' \right)\,\xrightarrow{{{Đ}_{B}}}\,\left( P'' \right) \\  M\,\,\xrightarrow{{{Đ}_{A}}}\,\,\,M'\xrightarrow{{{Đ}_{B}}}\,M'' \\ \end{align}\)

Do đó \(M''\in \left( P'' \right)\) , vậy phương trình (P’’) có dạng \(y={{x}^{2}}-8x+12\)

Chọn C.

Phương pháp giải:

Gọi K là điểm xác định bởi \(\overrightarrow{KA}+2\overrightarrow{KB}+3\overrightarrow{KC}=\overrightarrow{0}\), chứng minh \(K\equiv I\)

Từ giả thiết ban đầu, sử dụng công thức 3 điểm, chứng minh I là trung điểm của PQ, suy ra quỹ tích điểm Q khi P di động.

Lời giải chi tiết:

Gọi K là điểm xác định bởi \(\overrightarrow{KA}+2\overrightarrow{KB}+3\overrightarrow{KC}=\overrightarrow{0}\)

Khi đó  \(\overrightarrow{KA}+2\left( \overrightarrow{KA}+\overrightarrow{AB} \right)+3\left( \overrightarrow{KA}+\overrightarrow{AC} \right)=\overrightarrow{0}\Leftrightarrow 6\overrightarrow{AK}=2\overrightarrow{AB}+3\overrightarrow{AC}\Leftrightarrow \overrightarrow{AK}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\)

\(\begin{align}  \Rightarrow\overrightarrow{AK}=\overrightarrow{AE}+\overrightarrow{AF}=\overrightarrow{AI}\Rightarrow K\equiv I \\  \Rightarrow\overrightarrow{IA}+2\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0} \\\end{align}\)

Từ giả thiết ta có

\(\begin{align}  \overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=6\overrightarrow{IQ} \\  \Leftrightarrow \overrightarrow{PI}+\overrightarrow{IA}+2\overrightarrow{PI}+2\overrightarrow{IB}+3\overrightarrow{PI}+3\overrightarrow{IC}=6\overrightarrow{IQ} \\  \Leftrightarrow 6\overrightarrow{PI}+\underbrace{\left( \overrightarrow{IA}+2\overrightarrow{IB}+3\overrightarrow{IC} \right)}_{\overrightarrow{0}}=6\overrightarrow{IQ} \\  \Leftrightarrow \overrightarrow{PI}=\overrightarrow{IQ} \\ \end{align}\)

\(\Rightarrow I\) là trung điểm của PQ \(\Rightarrow \) Đ\(_{I}\left( P \right)=Q\Rightarrow \) Khi P di động trên (O) thì Q di động trên đường tròn (O’) là ảnh của (O) qua phép đối xứng tâm I.

Chọn A.

Phương pháp giải:

Phép đối xứng tâm I biến trọng tâm tam giác \(ABC\) thành trọng tâm tam giác\(A'B'C'\).

Lời giải chi tiết:

\(A\left( { - 1;2} \right),\,B\left( {3;4} \right),\,C\left( {4; - 3} \right) \Rightarrow \)Trọng tâm tam giác \(ABC\) là: \(G\left( {2;1} \right)\)

\( \Leftrightarrow \left\{ \begin{array}{l}2 + x' = 2.1\\1 + y' = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 0\\y' = 3\end{array} \right.\,\,\,\, \Rightarrow G'\left( {0;3} \right)\)

Chọn: D

Phương pháp giải:

Lời giải chi tiết:

Lấy \(A\left( {0;1} \right) \in d\), \(B\left( {0; - 4} \right) \in d'\).

Vậy trung điểm \(I\) của đoạn \(AB\) là tâm đối xứng biến \(d\) thành \(d'\)\( \Rightarrow I\left( {\dfrac{{0 + 0}}{2};\dfrac{{1 + \left( { - 4} \right)}}{2}} \right) \Leftrightarrow I\left( {0;\dfrac{{ - 3}}{2}} \right)\).

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}x' = 2.1 - x = 2 - x\\y' = 2.2 - y = 4 - y\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2 - x'\\y = 4 - y'\end{array} \right.\).

\(M' = {D_I}\left( M \right)\)\( \Rightarrow M':\,\,\left\{ \begin{array}{l}x' = 2 - \left( { - 2} \right) = 4\\y' = 4 - 3 = 1\end{array} \right.\)\( \Rightarrow M'\left( {4;1} \right)\).

\(\left( {C'} \right) = {D_I}\left( C \right)\)\( \Rightarrow {\left( {2 - x'} \right)^2} + {\left( {4 - y'} \right)^2} + 2\left( {2 - x'} \right) - 6\left( {4 - y'} \right) + 6 = 0\)

\( \Leftrightarrow x{'^2} + y{'^2} - 6x' - 2y' + 6 = 0\).

Vậy \(\left( {C'} \right):\,\,{x^2} + {y^2} - 6x - 2y + 6 = 0\).

Chọn B.

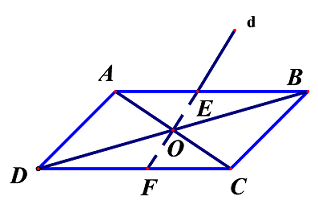
Phương pháp giải:

Lời giải chi tiết:

\(\left\{ \begin{array}{l}{x_{A'}} =  - {x_A} = 1\\{y_{A'}} =  - {y_A} =  - 3\end{array} \right. \Rightarrow A'\left( {1; - 3} \right)\).

Ta có:  \(\left\{ \begin{array}{l}x' =  - x\\y' =  - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - x'\\y =  - y'\end{array} \right.\)

\( \Rightarrow  - x' + 2y' + 3 = 0 \Leftrightarrow x' - 2y' - 3 = 0\).

Vậy phương trình đường thẳng \(d':\,\,x - 2y - 3 = 0\).

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

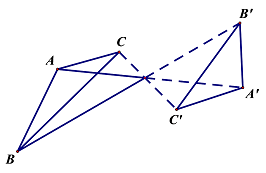
Gọi \(d\) là đường thẳng qua \(O\) và vuông góc với \(AB\) \( \Rightarrow EF \bot AB\)

Mà \(AB\parallel CD\) (tính chất hình bình hành) \( \Rightarrow EF \bot CD\)

Các cặp điểm trên hình vẽ đối xứng với nhau qua tâm \(O\) là:

      +) \(A\) đối xứng với \(C\) qua \(O\).

      +) \(B\) đối xứng với \(D\) qua \(O\).

            +) \(C\) đối xứng với \(F\) qua \(O\).

Phương pháp giải:

Lời giải chi tiết:

Ảnh của tam giác \(ABC\) qua phép đối xứng tâm \(E\) là tam giác \(A'B'C'\).

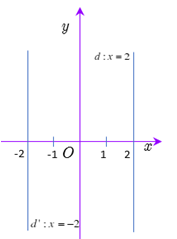
Phương pháp giải:

Lời giải chi tiết:

Phép đối xứng biến đường thẳng thành đường thẳng song song với nó

+ Gọi đường thẳng \(d'\) có ảnh là \(d \Rightarrow d'\parallel d\).

\( \Rightarrow d'\) có dạng: \(x - y + c = 0\)

+ Chọn điểm \(A\left( {0;4} \right) \in d\).

+ Phép đối xứng tâm \(I\) biến điểm \(A\) thuộc \(d\) thành \(A'\) thuộc \(d'\) \( \Rightarrow I\) là trung điểm của \(AA'\).

\( \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_{A'}}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_{A'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 2{x_I} - {x_A}\\{y_{A'}} = 2{y_I} - {y_A}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 8\\{y_{A'}} =  - 2\end{array} \right. \Rightarrow A'\left( {8; - 2} \right)\).

Vì \(A' \in d'\), thay điểm \(A'\) vào \(d'\) ta có: \(8 - \left( { - 2} \right) + c = 0 \Leftrightarrow c =  - 10\).

Vậy phương trình đường thẳng \(d':\,\,x - y - 10 = 0\).

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

Từ hình vẽ ta thấy ảnh của \(d\) trong phép đối xứng tâm \(O\left( {0;0} \right)\) là đường thẳng \(d':x =  - 2\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

“TRÍ ĐỨC” có chữ I có tâm đối xứng.

Chọn B.