30 bài tập trắc nghiệm đường tiệm cận của đồ thị hàm số mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\). Tìm tất cả các giá trị của \(m\) sao cho đồ thị hàm số có đúng hai đường tiệm cận đứng.
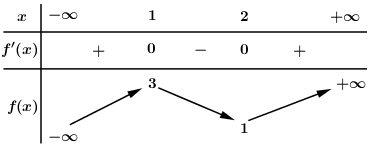
Đáp án: A Phương pháp giải: Số tiệm cận đứng của đồ thị hàm số đã cho bằng số nghiệm của mẫu thức mà không là nghiệm của tử thức. Lời giải chi tiết: Để đồ thị hàm số có 2 TCĐ thì phương trình \(f\left( x \right) = {x^2} - 8x + 2m = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(0 \le {x_1} < {x_2} \le 6\). \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\af\left( 0 \right) \ge 0\\af\left( 6 \right) \ge 0\\0 < \dfrac{S}{2} < 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}16 - 2m > 0\\1.2m \ge 0\\1.\left( { - 12 + 2m} \right) \ge 0\\0 < \dfrac{8}{2} < 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 8\\m \ge 0\\m \ge 6\end{array} \right. \Leftrightarrow 6 \le m < 8\) Vậy \(m \in \left[ {6;8} \right)\). Chọn A. Câu hỏi 2 : Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau: Số đường tiệm cận của đồ thị hàm số \(g\left( x \right) = \dfrac{1}{{2f\left( x \right) - 3}}\) là:
Đáp án: B Phương pháp giải: Sử dụng định nghĩa đường tiệm cận của đồ thị hàm số: Cho hàm số \(y = f\left( x \right)\). - Đường thẳng \(y = {y_0}\) được gọi là TCN của đồ thị hàm số nếu thỏa mãn một trong các điều kiện \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\), \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\). - Đường thẳng \(x = {x_0}\) được gọi là TCĐ của đồ thị hàm số nếu thỏa mãn một trong các điều kiện \(\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = - \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = - \infty \). Lời giải chi tiết: Dựa vào BBT ta thấy: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty ,\,\,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \). Khi đó ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{2f\left( x \right) - 3}} = 0\\\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{2f\left( x \right) - 3}} = 0\end{array}\) Do đó đồ thị hàm số \(y = g\left( x \right)\) có TCN \(y = 0\). Dựa vào BBT ta lại thấy: Phương trình \(2f\left( x \right) - 3 = 0 \Leftrightarrow f\left( x \right) = \dfrac{3}{2}\) có 3 nghiệm phân biệt, và 3 nghiệm này không bị triệt tiêu bởi nghiệm của tử. Do đó đồ thị hàm số có 3 đường tiệm cận đứng. Vậy đồ thị hàm số \(g\left( x \right) = \dfrac{1}{{2f\left( x \right) - 3}}\) có tất cả 4 đường tiệm cận. Chọn B. Câu hỏi 3 : Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 100;100} \right]\) để đồ thị hàm số \(y = \dfrac{1}{{\left( {x - m} \right)\sqrt {2x - {x^2}} }}\) có đúng 2 tiệm cận?
Đáp án: A Phương pháp giải: - Tìm ĐKXĐ của hàm số. - Xác định số tiệm cận ngang của đồ thị hàm số, sử dụng khái niệm: Nếu \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\) thì đường thẳng \(y = {y_0}\) là TCN của đồ thị hàm số \(y = f\left( x \right)\). - Suy ra đồ thị hàm số cần có bao nhiêu đường tiệm cận đứng ứng với bấy nhiêu nghiệm của mẫu thỏa mãn ĐKXĐ. Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}x - m \ne 0\\2x - {x^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne m\\0 < x < 2\end{array} \right.\). Do đó không tồn tại giới hạn của hàm số khi \(x \to \pm \infty \), do đó đồ thị hàm số không có tiệm cận ngang. Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} y = \infty ,\,\,\mathop {\lim }\limits_{x \to {2^ - }} y = \infty \), suy ra đồ thị hàm số có 2 tiệm cận đứng \(x = 0,\,\,x = 2\,\,\forall m\). Suy ra để đồ thị hàm số có đúng 2 đường tiệm cận thì \(m \notin \left( {0;2} \right) \Leftrightarrow \left[ \begin{array}{l}m \le 0\\m \ge 2\end{array} \right.\). Kết hợp điều kiện đề bài ta có \(m \in \left[ { - 100;0} \right] \cup \left[ {2;100} \right]\), \(m\) nguyên. Vậy có 101 + 99 = 200 giá trị của \(m\) thỏa mãn yêu cầu bài toán. Chọn A. Câu hỏi 4 : Biết đồ thị hàm số \(y = \dfrac{{\sqrt {x + 3} + ax + b}}{{{{\left( {x - 1} \right)}^2}}}\) không có đường tiệm cận đứng nào. Tính \(T = a - 3b.\)
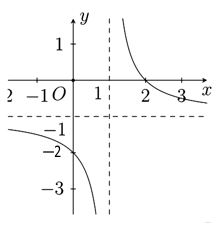
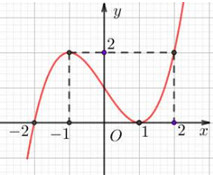
Đáp án: D Phương pháp giải: Đặt ẩn phụ\(t = \sqrt {x + 3} \), đưa hàm số về dạng bậc hai trên bậc hai rồi biện luận. Lời giải chi tiết: Ta có \(y = \dfrac{{\sqrt {x + 3} + ax + b}}{{{{\left( {x - 1} \right)}^2}}}\) Đặt \(\sqrt {x + 3} = t \Rightarrow x = {t^2} - 3\) Khi đó \(y = \dfrac{{a\left( {{t^2} - 3} \right) + t + b}}{{{{\left( {x - 1} \right)}^2}}}\) Để hàm số \(y = \dfrac{{\sqrt {x + 3} + ax + b}}{{{{\left( {x - 1} \right)}^2}}}\) không có tiệm cận đứng thì phương trình \(a\left( {{t^2} - 3} \right) + t + b = 0 \Leftrightarrow a{t^2} + t - 3a + b = 0\) có nghiệm kép \(t = 2\) (ứng với \(x = 1\)). Khi đó \(\left\{ \begin{array}{l}\Delta = 1 - 4a\left( {b - 3a} \right) = 0\\ - \dfrac{1}{{2a}} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{1}{4}\\b = - \dfrac{7}{4}\end{array} \right.\). Vậy \(T = a - 3b = - \dfrac{1}{4} - 3.\dfrac{{ - 7}}{4} = 5.\) Chọn D. Câu hỏi 5 : Đồ thị trong hình bên là của hàm số \(y = \dfrac{{ax + b}}{{x + c}}\)(với \(a,b,c \in \mathbb{R}\)). Khi đó tổng \(a + b + c\) bằng
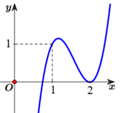
Đáp án: D Phương pháp giải: - Dựa vào đồ thị hàm số suy ra các đường tiệm cận để tìm a;c. - Dựa vào điểm thuộc đồ thị để tìm b. Lời giải chi tiết: Dựa vào hàm số ta có: Đồ thị hàm số có TCN \(y = a\) và TCĐ \(x = - c\). Dựa vào đồ thị hàm số ta có: Đồ thị hàm số có TCN \(y = - 1\) và TCĐ \(x = 1\). \( \Rightarrow \left\{ \begin{array}{l}a = - 1\\ - c = 1\end{array} \right. \Leftrightarrow a = c = - 1\). Khi đó hàm số có dạng \(y = \dfrac{{ - x + b}}{{x - 1}}\). Đồ thị hàm số đi qua điểm có tọa độ là \(\left( {2;0} \right) \Rightarrow 0 = \dfrac{{ - 2 + b}}{{2 - 1}} \Leftrightarrow b = 2.\) Vậy \(a + b + c = - 1 + 2 - 1 = 0.\) Chọn D. Câu hỏi 6 : Cho hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\). Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Đáp án: A Phương pháp giải: +) Đường thẳng \(x = a\) được gọi là TCĐ của đồ thị hàm số \(y = f\left( x \right)\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \infty .\) +) Đường thẳng \(y = b\) được gọi là TCN của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to \infty } f\left( x \right) = b.\) Lời giải chi tiết: Xét hàm số: \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\) TXĐ: \(D = \left( {2; + \infty } \right)\backslash \left\{ {\dfrac{7}{2}} \right\}.\) \(\mathop {\lim }\limits_{x \to \frac{7}{2}} \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\) \( = \mathop {\lim }\limits_{x \to \frac{7}{2}} \dfrac{1}{{\sqrt {x - 2} \left( {x + 2} \right)\left( {2x - 7} \right)}} = \infty \) \( \Rightarrow x = \dfrac{7}{2}\) là đường TCĐ của đồ thị hàm số. \(\mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}} = \mathop {\lim }\limits_{x \to 2} \dfrac{1}{{\left( {x + 2} \right)\sqrt {x - 2} \left( {2x - 7} \right)}} = \infty \) \( \Rightarrow x = 2\) là đường TCĐ của đồ thị hàm số. \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\) \( = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{\sqrt {x - 2} \left( {x + 2} \right)\left( {2x - 7} \right)}} = 0\) \( \Rightarrow y = 0\) là TCN của đồ thị hàm số. Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận. Chọn A. Câu hỏi 7 : Gọi \(S\) là tập hợp các giá trị nguyên \(m\) để đồ thị hàm số \(y = \dfrac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là:
Đáp án: C Phương pháp giải: - Tìm ĐKXĐ của hàm số. - Tìm điều kiện để phương trình \({x^2} - 6x + 2m = 0\) có hai nghiệm phân biệt thỏa mãn điều kiện xác định của tử và không bị triệt tiêu bởi nghiệm của tử. Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}x + 2 \ge 0\\{x^2} - 6x + 2m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\{x^2} - 6x + 2m > 0\end{array} \right.\). Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình \({x^2} - 6x + 2m = 0\) có 2 nghiệm phân biệt thỏa mãn \({x_1} > {x_2} > - 2\). \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1} + {x_2} > - 4\\\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 2m > 0\\6 > - 4\,\,\left( {luôn\,\,đúng} \right)\\{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < \frac{9}{2}\\2m + 2.6 + 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < \frac{9}{2}\\2m > - 16\end{array} \right.\\ \Leftrightarrow - 8 < m < \frac{9}{2}\\ \Rightarrow S = \left\{ { - 7; - 6; - 5; - 4; - 3; - 2; - 1;0;1;2;3;4} \right\}\end{array}\) Vậy tập hợp \(S\) có 12 phần tử. Chọn C. Câu hỏi 8 : Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = m.\) Có bao nhiêu giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có duy nhất một tiệm cận ngang.
Đáp án: C Phương pháp giải: Định nghĩa tiệm cận ngang của đồ thị hàm số \(y = f(x)\). Nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = a\,\)hoặc\(\,\mathop {\lim }\limits_{x \to - \infty } f(x) = a \Rightarrow y = a\) là TCN của đồ thị hàm số. Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{f\left( x \right) + 2}} = \dfrac{1}{{\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to - \infty } 2}} = \dfrac{1}{{ - 1 + 2}} = 1 \Rightarrow \) Đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có TCN \(y = 1\) \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) + 2}} = \dfrac{1}{{\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to + \infty } 2}} = \dfrac{1}{{m + 2}}\). Để đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có duy nhất một tiệm cận ngang thì \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) + 2}}\) hoặc là không xác định hoặc là bằng 1. Khi đó \(\left[ \begin{array}{l}m + 2 = 0\\m + 2 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 2\\m = - 1\end{array} \right.\). Vậy có 2 giá trị thực của \(m\) thỏa mãn yêu cầu bài toán. Chọn C. Câu hỏi 9 : Cho hàm số \(f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), có bảng biến thiên như sau:
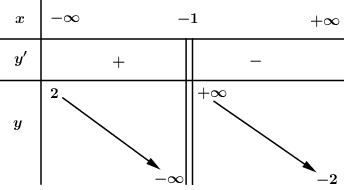
Hỏi đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right)}}\)có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Đáp án: A Phương pháp giải: Dựa vào định ngĩa đường tiệm cận của đồ thị hàm số \(y = f\left( x \right)\). - Đường thẳng \(y = {y_0}\) được gọi là TCN của đồ thị hàm số khi thỏa mãn một trong các điều kiện: \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\), \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\). - Đường thẳng \(x = {x_0}\) được gọi là TCĐ của đồ thị hàm số khi thỏa mãn một trong các điều kiện: \(\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = - \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = - \infty \). Lời giải chi tiết: Dựa vào BBT ta có: \(\mathop {\lim }\limits_{x \to - \infty } y = 2\), \(\mathop {\lim }\limits_{x \to + \infty } y = - 2\), \(\mathop {\lim }\limits_{x \to - {1^ - }} y = - \infty \), \(\mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \). Đặt \(y = g\left( x \right) = \dfrac{1}{{f\left( x \right)}}\) ta có: \(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right)}} = - \dfrac{1}{2}\) \( \Rightarrow y = - \dfrac{1}{2}\) là TCN của đồ thị hàm số \(y = g\left( x \right) = \dfrac{1}{{f\left( x \right)}}\). \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{f\left( x \right)}} = \dfrac{1}{2}\) \( \Rightarrow y = \dfrac{1}{2}\) là TCN của đồ thị hàm số \(y = g\left( x \right) = \dfrac{1}{{f\left( x \right)}}\). \(\mathop {\lim }\limits_{x \to - 1} g\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \dfrac{1}{{f\left( x \right)}} = 0\) \( \Rightarrow x = - 1\) không là TCĐ của đồ thị hàm số \(y = g\left( x \right) = \dfrac{1}{{f\left( x \right)}}\). Xét phương trình \(f\left( x \right) = 0\), dựa vào BBT ta thấy phương trình có 2 nghiệm phân biệt thỏa mãn khác \( - 1\). Do đó đồ thị hàm số \(y = g\left( x \right) = \dfrac{1}{{f\left( x \right)}}\) có 2 TCĐ. Vậy đồ thị hàm số \(y = g\left( x \right) = \dfrac{1}{{f\left( x \right)}}\) có tất cả 4 đường tiệm cận. Chọn A. Câu hỏi 10 : Cho hàm số \(y = \dfrac{{3x + 1}}{{x - 4}}\) có đồ thị \(\left( C \right)\), với mọi điểm \(M\) thuộc \(\left( C \right)\) thì tích các khoảng cách từ \(M\) tới 2 đường tiệm cận của \(\left( C \right)\) bằng:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đồ thị hàm số \(y = \dfrac{{3x + 1}}{{x - 4}}\) (C) có TCĐ là: \(x = 4\), TCN là: \(y = 3\) Lấy điểm \(M\) bất kì thuộc (C), giả sử \(M\left( {{x_0};\dfrac{{3{x_0} + 1}}{{{x_0} - 4}}} \right)\,\,\left( {{x_0} \ne 4} \right)\). Tích khoảng cách từ M tới 2 đường tiệm cận là: \(\left| {{x_0} - 4} \right|.\left| {\dfrac{{3{x_0} + 1}}{{{x_0} - 4}} - 3} \right| = \left| {{x_0} - 4} \right|.\left| {\dfrac{{13}}{{{x_0} - 4}}} \right| = 13\) Chọn D. Câu hỏi 11 : Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x\sqrt {2 - {x^2}} }}{{{x^2} + x - 2}}\) là
Đáp án: A Phương pháp giải: - Tìm TXĐ của hàm số. - Sử dụng định nghĩa các đường tiệm cận: Cho hàm số \(y = f\left( x \right)\). + Đường thẳng \(y = {y_0}\) là TCN của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\). + Đường thẳng \(x = {x_0}\) là TCĐ của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = - \infty \) , \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to x_0^ - } y = - \infty \). Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}2 - {x^2} \ge 0\\{x^2} + x - 2 \ne 0\end{array} \right. \Leftrightarrow x \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\backslash \left\{ 1 \right\}\). Do đó hàm số không có tiệm cận ngang (do không thể tồn tại giới hạn khi x tiến ra vô cực). Ta xét \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{x\sqrt {2 - {x^2}} }}{{{x^2} + x - 2}} = + \infty \\\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{x\sqrt {2 - {x^2}} }}{{{x^2} + x - 2}} = - \infty \end{array} \right.\). (Ta không xét giới hạn của hàm số khi \(x \to {2^ + }\) và \(x \to {2^ - }\) do \(x = 2\) không thuộc TXĐ của hàm số). Do đó \(x = 1\) là TCĐ của đồ thị hàm số. Vậy đồ thị hàm số có 1 tiệm cận đứng. Chọn A. Câu hỏi 12 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
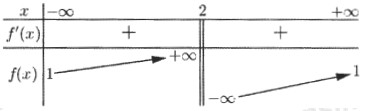
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) - 1}}\) là
Đáp án: B Phương pháp giải: Sử dụng định nghĩa về đường tiệm cận Lời giải chi tiết: Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) - 1}} = \dfrac{1}{{2 - 1}} = 1\), do đó đồ thị hàm số có TCN \(y = 1\). \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{f\left( x \right) - 1}} = 0\), do đó đồ thị hàm số có TCN \(y = 0\). Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) - 1}}\) là số nghiệm của phương trình \(f\left( x \right) = 1.\) Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 4 điểm phân biệt nên phương trình \(f\left( x \right) = 1\) có 4 nghiệm phân biệt. Suy ra đồ thị hàm số có 4 đường tiệm cận đứng. Vậy đồ thị hàm số có tổng cộng 6 đường tiệm cận. Chọn B. Câu hỏi 13 : Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 10;10} \right]\) để đồ thị hàm số \(y = \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}}\) có ba đường tiệm cận?
Đáp án: A Phương pháp giải: - Đồ thị hàm số \(y = f\left( x \right)\) nhận đường thẳng \(x = a\) là tiệm cận đứng khi xảy ra một trong các giới hạn \(\mathop {\lim }\limits_{x \to {a^ \pm }} f\left( x \right) = \pm \infty \). - Đồ thị hàm số \(y = f\left( x \right)\) nhận đường thẳng \(y = b\) là tiệm cận ngang khi xảy ra một trong các giới hạn \(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b\). Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}m{x^2} \ge 4\\x \ne 1\end{array} \right.\) \( \Rightarrow m > 0\). Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}} = \sqrt m \\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}} = - \sqrt m \end{array} \right. \Rightarrow \) Đồ thị hàm số có 2 đường tiệm cận ngang \(y = \pm \sqrt m \) \(\left( {m > 0} \right)\). Để đồ thị hàm số \(y = \dfrac{{\sqrt {m{x^2} - 4} }}{{x - 1}}\) có 3 đường tiệm cận thì đồ thị hàm số phải có 1 đường tiệm cận đứng. \( \Rightarrow x = 1\) phải thỏa mãn điều kiện \(m{x^2} \ge 4 \Leftrightarrow m \ge 4\). Do đó, \(m \ge 4\) thì hàm số đã cho có 1 đường tiệm cận đứng và 2 đường tiệm cận ngang. Mặt khác \(m \in \left[ { - 10;10} \right]\), \(m \in \mathbb{Z}\) nên \(m \in \left\{ {4;5;6;7;8;9;10} \right\}\). Vậy có tất cả 7 giá trị nguyên của tham số \(m\) thỏa mãn bài toán. Chọn A. Câu hỏi 14 : Cho hàm số \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\,\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
Trong các số \(a,\,\,b\) và \(c\) có bao nhiêu số dương ?
Đáp án: C Phương pháp giải: Từ BBT suy ra các đường TCĐ, TCN của đồ thị hàm số. Từ đó suy ra mối quan hệ của \(a,\,\,b,\,\,c.\) Lời giải chi tiết: Dựa vào BBT ta thấy đồ thị hàm số có TCĐ: \(x = 2\) \( \Rightarrow - \dfrac{c}{b} = 2 \Leftrightarrow c = - 2b\) TCN: \(y = 1 \Rightarrow \dfrac{a}{b} = 1 \Leftrightarrow a = b\) Ta có: \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\) \( \Rightarrow f'\left( x \right) = \dfrac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}}\) Hàm số đồng biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\) \(\begin{array}{l} \Leftrightarrow y' > 0\,\,\,\,\,\forall x \ne 2\\ \Leftrightarrow \dfrac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}} > 0\,\,\,\forall x \ne 2\\ \Leftrightarrow ac - b > 0\\ \Leftrightarrow b.\left( { - 2b} \right) - b > 0\\ \Leftrightarrow - 2{b^2} - b > 0\\ \Leftrightarrow 2{b^2} + b < 0\\ \Leftrightarrow - \dfrac{1}{2} < b < 0\\ \Rightarrow b < 0\\ \Rightarrow a < 0,c > 0\end{array}\) Vậy trong ba số \(a,\,\,b,\,\,c\) có 1 số dương. Chọn C. Câu hỏi 15 : Số giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\) có 3 tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) là
Đáp án: C Phương pháp giải: Đường thẳng \(x = a\) được gọi là TCĐ của đồ thị hàm số \(y = f\left( x \right) = \frac{{g\left( x \right)}}{{h\left( x \right)}}\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \infty .\) Đường thẳng \(y = b\) được gọi là TCN của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b.\) Lời giải chi tiết: Điều kiện: \(\left\{ \begin{array}{l}x \ge - 1\\{x^2} - \left( {1 - m} \right)x + 2m > 0\end{array} \right..\) Ta có: \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\) Đồ thị hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\)\(\left( {x \ge - 1} \right)\) có tiệm cận ngang là đường thẳng \(y = 0.\) Do đó để hàm số có 3 đường tiệm cận thì hàm số phải có 2 tiệm cận đứng \( \Rightarrow {x^2} - \left( {1 - m} \right)x + 2m = 0\) có 2 nghiệm phân biệt lớn hơn \( - 1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) > 0\\{x_1} + 1 + {x_2} + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {1 - m} \right)^2} - 8m > 0\\{x_1}{x_2} + \left( {{x_1} + {x_2}} \right) + 1 > 0\\{x_1} + {x_2} + 2 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {1 - m} \right)^2} - 8m > 0\\2m + 1 - m + 1 > 0\\1 - m + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 - 2m + {m^2} - 8m > 0\\m + 2 > 0\\m < 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 10m + 1 > 0\\m > - 2\\m < 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 5 + 2\sqrt 6 \\m < 5 - 2\sqrt 6 \end{array} \right.\\ - 2 < m < 3\end{array} \right. \Leftrightarrow - 2 < m < 5 - 2\sqrt 6 \\ \Rightarrow m \in \left\{ { - 1;0} \right\}\end{array}\) Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;\,\,0} \right\}.\) Chọn C. Câu hỏi 16 : Cho hàm số \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}}\). Số giá trị thực của \(m\) để đồ thị hàm số có đúng hai đường tiệm cận ?
Đáp án: B Phương pháp giải: - Sử dụng Định nghĩa tiệm cận ngang của đồ thị hàm số \(y = f(x)\): Nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = a\,\)hoặc\(\,\mathop {\lim }\limits_{x \to - \infty } f(x) = a\)\( \Rightarrow y = a\) là TCN của đồ thị hàm số, xác định đường TCN của hàm số. - Để hàm số có đúng hai đường tiệm cận thì hàm số phải có bao nhiêu đường tiệm cận đứng. - Tìm điều kiện số nghiệm của phương trình mẫu số = 0. Lời giải chi tiết: Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - x}}{{{x^2} - 2mx + 4}} = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 - x}}{{{x^2} - 2mx + 4}} = 0.\) \( \Rightarrow \) Đồ thị hàm số \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}}\) luôn có 1 TCN \(y = 0\) với mọi \(m\). Để đồ thị hàm số \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}}\) có đúng 2 đường tiệm cận thì số đường tiệm cận đứng là 1. \( \Leftrightarrow \) Phương trình \({x^2} - 2mx + 4 = 0\,\,\left( * \right)\) hoặc là có hai nghiệm phân biệt, trong đó có một nghiệm là 1; hoặc là có nghiệm kép (bằng 1 hay khác 1 đều nhận). TH1 : \(x = 1\) là nghiệm của phương trình (*) trên \( \Rightarrow 1 - 2m + 4 = 0 \Leftrightarrow m = \dfrac{5}{2}\). Khi đó \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}} = \dfrac{{1 - x}}{{{x^2} - 5x + 4}} = \dfrac{{ - 1}}{{x - 4}}\) \( \Rightarrow \) Đồ thị hàm số có đúng 1 TCĐ là \(x = 4 \Rightarrow m = \dfrac{5}{2}\) thỏa mãn. TH2 : Phương trình \({x^2} - 2mx + 4 = 0\) có nghiệm kép \( \Leftrightarrow \Delta = {m^2} - 4 = 0 \Leftrightarrow m = \pm 2.\) Thử lại: Với \(m = - 2\) thì \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}} = \dfrac{{1 - x}}{{{x^2} + 4x + 4}}\) có 1 TCĐ là \(x = - 2\). Với \(m = - 2\) thì \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}} = \dfrac{{1 - x}}{{{x^2} - 4x + 4}}\) có 1 TCĐ là \(x = 2\). \( \Rightarrow m = \pm 2\)thỏa mãn. Vậy tập các giá trị của \(m\) thỏa mãn là \(\left\{ {\dfrac{5}{2};2; - 2} \right\}.\) Chọn B. Câu hỏi 17 : Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên.
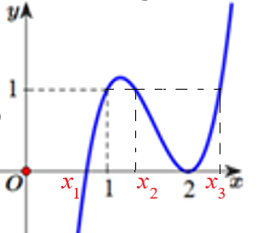
Hỏi đồ thị hàm số \(g(x) = \dfrac{{({x^2} - 3x + 2)\sqrt {x - 1} }}{{x\left[ {{f^2}(x) - f(x)} \right]}}\) có bao nhiêu tiệm cận đứng?
Đáp án: B Phương pháp giải: - Xác định số nghiệm của phương trình mẫu số. - Số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình mẫu số thỏa mãn điều kiện xác định và không bị triệt tiêu hết bởi nghiệm của tử số. Lời giải chi tiết:
ĐKXĐ: \(x \ge 1,\,\,f\left( x \right) \ne 0,\,\,f\left( x \right) \ne 1\). \(g(x) = \dfrac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}} = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.f\left( x \right)\left( {f\left( x \right) - 1} \right)}}\) Nhận xét: \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy: +) \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = {x_1}\,\,\left( {0 < {x_1} < 1} \right)\,\,\left( {ktm} \right)\)(nghiệm đơn) và \(x = 2\)(nghiệm kép). +) \(f\left( x \right) = 1\) có 3 nghiệm phân biệt \(x = 1\) (nghiệm đơn), \(x = {x_2}\,\,\left( {1 < {x_2} < 2} \right)\) (nghiệm đơn) và \(x = {x_3}\,\,\left( {{x_3} > 2} \right)\) (nghiệm đơn). Khi đó hàm số \(y = g\left( x \right)\) được viết dưới dạng : \(g\left( x \right) = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.\,a\left( {x - {x_1}} \right){{\left( {x - 2} \right)}^2}.\,a\left( {x - 1} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)}}\) Do đó, đồ thị hàm số \(g\left( x \right)\) có 3 đường tiệm cận đứng là: \(x = {x_2},\,\,x = 2,\,\,x = {x_3}.\) Chọn: B. Câu hỏi 18 : Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = \dfrac{{x - 1}}{{{x^2} + 2mx - m + 2}}\) có đúng hai đường tiệm cận. Tổng tất cả các phần tử của tập \(S\) bằng:
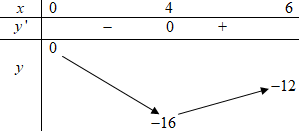
Đáp án: A Phương pháp giải: Đồ thị hàm số \(y = f\left( x \right)\) nhận đường thẳng \(x = a\) là tiệm cận đứng khi xảy ra một trong các giới hạn \(\mathop {\lim }\limits_{x \to {a^ \pm }} f\left( x \right) = \pm \infty \). Đồ thị hàm số \(y = f\left( x \right)\) nhận đường thẳng \(y = b\) là tiệm cận ngang khi xảy ra một trong các giới hạn \(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b\). Tìm đường tiệm cận ngang của đồ thị hàm số để suy ra số đường tiệm cận đứng. Từ đó tìm giá trị của \(m\) thỏa mãn. Lời giải chi tiết: Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{x - 1}}{{{x^2} + 2mx - m + 2}} = 0\). Do đó, đồ thị hàm số đã cho luôn nhận đường thẳng \(y = 0\) là tiệm cận ngang với mọi giá trị của \(m\). Đồ thị hàm số có đúng hai đường tiệm cận khi và chỉ khi nó có đúng 1 đường tiệm cận đứng. Đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình \({x^2} + 2mx - m + 2 = 0\) hoặc có nghiệm kép, hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng \(1\). (1) Phương trình \({x^2} + 2mx - m + 2 = 0\) có \(\Delta ' = {m^2} - \left( { - m + 2} \right) = {m^2} + m - 2\) \(\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}\Delta ' = 0\\\left\{ \begin{array}{l}\Delta ' > 0\\{1^2} + 2m.1 - m + 2 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} + m - 2 = 0\\\left\{ \begin{array}{l}{m^2} + m - 2 > 0\\3 + m = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\\\left\{ \begin{array}{l}m > 1\\m < - 2\\m = - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\\m = - 3\end{array} \right.\) Do đó, tập các giá trị của tham số \(m\) thỏa mãn là \(S = \left\{ {1; - 2; - 3} \right\}\). Vậy tổng tất cả các phần tử của tập hợp \(S\) bằng \(1 - 2 - 3 = - 4\). Chọn A. Câu hỏi 19 : Cho hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\). Tìm tất cả các giá trị của \(m\) sao cho đồ thị hàm số có đúng hai đường tiệm cận đứng.
Đáp án: A Phương pháp giải: - Tìm ĐKXĐ của hàm số. - Đồ thị hàm số có 2 đường tiệm cận đứng khi và chỉ khi phương trình mẫu số = 0 có 2 nghiệm phân biệt thỏa mãn ĐKXĐ. - Cô lập \(m\). Sử dụng phương pháp hàm số. Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}0 \le x \le 6\\{x^2} - 8x + 2m > 0\end{array} \right.\) Để đồ thị hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\) có hai đường tiệm cận đứng thì phương trình \({x^2} - 8x + 2m = 0\) có hai nghiệm phân biệt thuộc đoạn \(\left[ {0;6} \right]\) \( \Leftrightarrow \) Phương trình \({x^2} - 8x = - 2m\) có hai nghiệm phân biệt thuộc đoạn \(\left[ {0;6} \right]\)(*). Xét hàm số \(f\left( x \right) = {x^2} - 8x\) ta có: \(f'\left( x \right) = 2x - 8 = 0 \Leftrightarrow x = 4.\) Bảng biến thiên:
Dựa vào bảng biến thiên ta thì \(\left( * \right) \Leftrightarrow - 16 < - 2m \le - 12 \Leftrightarrow 6 \le m < 8.\) Vậy \(m \in \left[ {6;8} \right)\). Chọn A. Câu hỏi 20 : Cho hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\,\,\left( C \right)\). Biết rằng \({M_1}\left( {{x_1};{y_1}} \right)\) và \({M_2}\left( {{x_2};{y_2}} \right)\) là hai điểm trên đồ thị \(\left( C \right)\) có tổng khoản cách đến hai tiệm cận của \(\left( C \right)\) nhỏ nhất. Tính giá trị \(P = {x_1}{x_2} + {y_1}{y_2}\).
Đáp án: D Phương pháp giải: - Xác định các đường tiệm cận của đồ thị hàm số. - Gọi \(M\left( {a;\frac{{2a - 1}}{{a + 1}}} \right) \in \left( C \right)\) \(\left( {a \ne - 1} \right)\). Tính các khoảng cách từ \(M\) đến hai đường tiệm cận. - Sử dụng BĐT Cô-si để tìm GTNN của tổng khoảng cách. Lời giải chi tiết: TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\). Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\,\,\left( C \right)\) có hai đường tiệm cận là \(y = 2;\,\,x = - 1\). Gọi \(M\left( {a;\dfrac{{2a - 1}}{{a + 1}}} \right) \in \left( C \right)\) \(\left( {a \ne - 1} \right)\). Khoảng cách từ \(M\) đến đường thẳng \(y = 2 \Leftrightarrow y - 2 = 0\) là: \({d_1} = \dfrac{{\left| {\dfrac{{2a - 1}}{{a + 1}} - 2} \right|}}{{\sqrt {{0^2} + {1^2}} }} = \left| {\dfrac{{2a - 1 - 2a - 2}}{{a + 1}}} \right|\)\( = \dfrac{3}{{\left| {a + 1} \right|}}\). Khoảng cách từ \(M\) đến đường thẳng \(x = - 1 \Leftrightarrow x + 1 = 0\) là: \({d_2} = \dfrac{{\left| {a + 1} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {a + 1} \right|\). Do đó tổng khoảng cách từ \(M\) đến hai đường tiệm cận là: \(d = {d_1} + {d_2} = \dfrac{3}{{\left| {a + 1} \right|}} + \left| {a + 1} \right|\) \( \ge 2\sqrt {\dfrac{3}{{\left| {a + 1} \right|}}.\left| {a + 1} \right|} = 2\sqrt 3 \) (BĐT Cô-si) Dấu “=” xảy ra \( \Leftrightarrow \dfrac{3}{{\left| {a + 1} \right|}} = \left| {a + 1} \right| \Leftrightarrow {\left( {a + 1} \right)^2} = 3\)\( \Leftrightarrow \left[ \begin{array}{l}a = - 1 + \sqrt 3 \\a = - 1 - \sqrt 3 \end{array} \right.\,\,\left( {tm} \right)\). Với \(a = - 1 + \sqrt 3 \) ta có \({M_1}\left( { - 1 + \sqrt 3 ;2 - \sqrt 3 } \right)\). Với \(a = - 1 - \sqrt 3 \) ta có \({M_2}\left( { - 1 - \sqrt 3 ;2 + \sqrt 3 } \right)\). Vậy \(\begin{array}{l}P = {x_1}{x_2} + {y_1}{y_2}\\\,\,\,\,\, = \left( { - 1 + \sqrt 3 } \right)\left( { - 1 - \sqrt 3 } \right) + \left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)\\\,\,\,\,\, = {\left( { - 1} \right)^2} - 3 + 4 - 3\\\,\,\,\,\, = - 1\end{array}\) Chọn D. Câu hỏi 21 : Cho hàm đa thức bậc ba \(y = f\left( x \right)\) có đò thị như hình vẽ
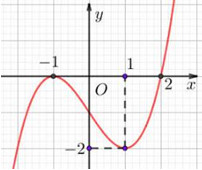
Tổng số đường tiệm cận ngang và đứng của đồ thị hàm số \(y = \dfrac{{\left( {x + 1} \right)\left( {{x^2} - 1} \right)}}{{f\left( x \right)}}\) là
Đáp án: B Phương pháp giải: Cho hàm số \(y = f\left( x \right)\): - Đồ thị hàm số nhận \(y = {y_0}\) làm TCN nếu thỏa mãn một trong các điều kiện \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\), \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\). - Đồ thị hàm số nhận \(x = {x_0}\) làm TCĐ nếu thỏa mãn một trong các điều kiện \(\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = - \infty \). Lời giải chi tiết: Hàm số có dạng \(f\left( x \right) = a{x^3} + b{x^2} + cx - 1\) (vì là hàm bậc ba và cắt trục tung tại điểm có tung độ \( - 1\)) Đồ thị hàm số đã cho đi qua các điểm có tọa độ là \(\left( { - 1;0} \right),\,\,\left( {1; - 2} \right);\,\,\left( {2;0} \right)\). \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}8a + 4b + 2c = 1\\ - a + b - c = 1\\a + b + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = 0\\c = \dfrac{{ - 3}}{2}\end{array} \right.\\ \Rightarrow f\left( x \right) = \dfrac{1}{2}{x^3} - \dfrac{3}{2}x - 1 = \dfrac{1}{2}{\left( {x - 1} \right)^2}\left( {x - 2} \right)\end{array}\) Khi đó \(y = \dfrac{{\left( {x + 1} \right)\left( {{x^2} - 1} \right)}}{{f\left( x \right)}} = \dfrac{{\left( {x + 1} \right)\left( {{x^2} - 1} \right)}}{{\dfrac{1}{2}{{\left( {x - 1} \right)}^2}\left( {x - 2} \right)}} = \dfrac{{2{{\left( {x + 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x - 2} \right)}}\) Đồ thị hàm số trên có tiệm cận ngang \(y = 2\) và tiệm cận đứng là \(x = 1,\,\,x = 2\). Vậy đồ thị hàm số \(y = \dfrac{{\left( {x + 1} \right)\left( {{x^2} - 1} \right)}}{{f\left( x \right)}}\) có 3 đường tiệm cận. Chọn B. Câu hỏi 22 : Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có đồ thị như hình dưới đây.
Gọi \(S\) là tập các giá trị nguyên của m thuộc khoảng (-2019 ;2020) để đồ thị hàm số \(g\left( x \right) = \dfrac{{\left( {x + 1} \right)\sqrt {f\left( x \right)} }}{{\left( {f\left( x \right) - 2} \right)\left( {{x^2} - 2mx + m + 2} \right)}}\) có 5 đường tiệm cận ( tiệm cận đứng hoặc tiệm cận ngang). Số phần tử của \(S\) là:
Đáp án: A Phương pháp giải: - Dựa vào đồ thị để tìm nghiệm của phương trình \(f\left( x \right) = 2\). - Biện luận để tìm điều kiện của \(m\). Lời giải chi tiết: Đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\) cắt trục tung tại điểm có tung độ bằng 1; đi qua các điểm có tọa độ \(\left( {1;0} \right),\,\,\left( {2;2} \right);\,\,\left( { - 1;2} \right)\). \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}d = 1\\a + b + c + d = 0\\8a + 4b + 2c + d = 2\\ - a + b - c + d = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = 0\\c = \dfrac{{ - 3}}{2}\end{array} \right.\\ \Rightarrow f\left( x \right) = \dfrac{1}{2}{x^3} - \dfrac{3}{2}x + 1 = \dfrac{1}{2}{\left( {x - 1} \right)^2}\left( {x + 2} \right)\end{array}\) Khi đó \(\begin{array}{l}g\left( x \right) = \dfrac{{\left( {x + 1} \right)\sqrt {f\left( x \right)} }}{{\left( {f\left( x \right) - 2} \right)\left( {{x^2} - 2mx + m + 2} \right)}}\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\left( {x + 1} \right)\sqrt {\dfrac{1}{2}{{\left( {x - 1} \right)}^2}\left( {x + 2} \right)} }}{{\dfrac{1}{2}\left( {x - 2} \right){{\left( {x + 1} \right)}^2}\left( {{x^2} - 2mx + m + 2} \right)}}\,\,\,\left( {x \ge - 2} \right)\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\sqrt {\dfrac{1}{2}{{\left( {x - 1} \right)}^2}\left( {x + 2} \right)} }}{{\dfrac{1}{2}\left( {x - 2} \right)\left( {x + 1} \right)\left( {{x^2} - 2mx + m + 2} \right)}}\,\,\left( {x \ge - 2} \right)\end{array}\) Đồ thị hàm số có 1 đường TCN là \(y = 0\). Để đồ thị hàm số có 5 đường tiệm cận thì phương trình \({x^2} - 2mx + m + 2 = 0\) phải có 2 nghiệm phân biệt khác \(2,\,\, - 1,\,\,1\) và thỏa mãn lớn hơn hoặc bằng \( - 2\). \( \Rightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - m - 2 > 0\\1 - 2m + m + 2 \ne 0\\1 + 2m + m + 2 \ne 0\\4 - 4m + m + 2 \ne 0\\{x_1} + {x_2} = 2m > - 4\\\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m \notin \left\{ {3; - 1;2} \right\}\\m > - 2\\m + 2 + 2.2m + 4 \ge 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\ - 2 < m < - 1\end{array} \right.\\m \ne 3\\m \ge - \dfrac{6}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\ - \dfrac{6}{5} \le m < - 1\end{array} \right.\\m \ne 3\end{array} \right.\) Kết hợp điều kiện \(m \in \left( { - 2019;2020} \right),\,\,m \in \mathbb{Z}\) \( \Rightarrow \left\{ \begin{array}{l}3 < m < 2020\\n \in \mathbb{Z}\end{array} \right. \Rightarrow \) Có 2016 giá trị \(m\) thỏa mãn yêu cầu bài toán. Chọn A. Câu hỏi 23 : Có bao nhiêu giá trị nguyên của \(m\) để đồ thị hàm số \(y = \frac{{x - 2}}{{{x^2} - 3mx + m}}\) có đúng một tiệm cận đứng?
Đáp án: A Phương pháp giải: Đường thẳng \(x = a\) được gọi là TCĐ của đồ thị hàm số \(y = f\left( x \right) = \frac{{g\left( x \right)}}{{h\left( x \right)}}\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \infty .\) Lời giải chi tiết: Ta có: \(y = \frac{{x - 2}}{{{x^2} - 3mx + m}}\) Điều kiện: \({x^2} - 3mx + m \ne 0.\) Đồ thị hàm số \(y = \frac{{x - 2}}{{{x^2} - 3mx + m}}\) có đúng một tiệm cận đứng \( \Leftrightarrow \) phương trình \(g\left( x \right) = {x^2} - 3mx + m = 0\) có hai nghiệm phân biệt trong đó có một nghiệm \(x = 2\) hoặc phương trình có nghiệm kép \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\Delta > 0\\g\left( 2 \right) = 0\end{array} \right.\\\Delta = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}9{m^2} - 4m > 0\\{2^2} - 3m.2 + m = 0\end{array} \right.\\9{m^2} - 4m = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m\left( {9m - 4} \right) > 0\\5m = 4\end{array} \right.\\m\left( {9m - 4} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\left[ \begin{array}{l}m < 0\\m > \frac{4}{9}\end{array} \right.\\m = \frac{4}{5}\end{array} \right.\\m = 0\\m = \frac{4}{9}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \frac{4}{5}\\m = 0\\m = \frac{4}{9}\end{array} \right..\) Mà \(m \in \mathbb{Z} \Rightarrow m = 0 \Rightarrow \) có 1 giá trị nguyên thỏa mãn bài toán. Chọn A. Câu hỏi 24 : Xác định số đường đường tiệm cận của đồ thị hàm số \(y = \dfrac{{\sqrt {x + 4} - 2}}{{{x^2} + 5x}}\).
Đáp án: D Phương pháp giải: Tính \(f\left( x \right) - f\left( { - x} \right)\,\,\forall x \in \left[ {1;100} \right]\) sau đó tính \({S_1} - {S_2}\) Lời giải chi tiết: TXĐ: \(D = \left[ { - 4; + \infty } \right)\backslash \left\{ 0 \right\}\). Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {x + 4} - 2}}{{{x^2} + 5x}} = 0\) \( \Rightarrow y = 0\) là đường tiệm cận đứng của đồ thị hàm số. \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sqrt {x + 4} - 2}}{{{x^2} + 5x}} = \dfrac{1}{{20}}\\\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sqrt {x + 4} - 2}}{{{x^2} + 5x}} = \dfrac{1}{{20}}\end{array}\) \( \Rightarrow \) Đồ thị hàm số không có TCĐ. Chọn D. Câu hỏi 25 : Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{\left( {\sqrt {x + 1} - 2} \right)\sin x}}{{{x^3} - {x^2} - 6x}}\) là
Đáp án: B Phương pháp giải: - Đồ thị hàm số y = f(x) nhận đường thẳng \(x = {x_0}\) là TCĐ khi thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = - \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = - \infty \). - Tính giới hạn bẳng phương pháp nhân cả tử và mẫu với biểu thức liên hợp, và sử dụng giới hạn \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1\). Lời giải chi tiết: ĐKXĐ: \(x + 1 \ge 0 \Leftrightarrow x \ge - 1\). Xét phương trình mẫu số: \(\begin{array}{l}\,\,\,\,\,\,{x^3} - {x^2} - 6x = 0\\ \Leftrightarrow x\left( {{x^2} - x - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,\,\left( {tm} \right)\\x = 3\,\,\,\,\,\,\left( {tm} \right)\\x = - 2\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Ta có: \(\begin{array}{l}y = \dfrac{{\left( {\sqrt {x + 1} - 2} \right)\sin x}}{{{x^3} - {x^2} - 6x}}\\y = \dfrac{{\left( {x + 1 - 4} \right)\sin x}}{{\left( {\sqrt {x + 1} + 2} \right)x\left( {x + 2} \right)\left( {x - 3} \right)}}\\y = \dfrac{{\sin x}}{{\left( {\sqrt {x + 1} + 2} \right)x\left( {x + 2} \right)}}\end{array}\) Khi đó: \(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sin x}}{{\left( {\sqrt {x + 1} + 2} \right)x\left( {x + 2} \right)}}\)\( = \dfrac{1}{{\left( {1 + 2} \right)\left( {0 + 2} \right)}}.1 = \dfrac{1}{6}\) \(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{\sin x}}{{\left( {\sqrt {x + 1} + 2} \right)x\left( {x + 2} \right)}}\)\( = \dfrac{1}{{\left( {1 + 2} \right)\left( {0 + 2} \right)}}.1 = \dfrac{1}{6}\) Suy ra x = 0 không là TCĐ của đồ thị hàm số. \(\mathop {\lim }\limits_{x \to {3^ + }} y\)\( = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\sin x}}{{\left( {\sqrt {x + 1} + 2} \right)x\left( {x + 2} \right)}}\)\( = \dfrac{{\sin 3}}{{60}}\). \(\mathop {\lim }\limits_{x \to {3^ - }} y\)\( = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\sin x}}{{\left( {\sqrt {x + 1} + 2} \right)x\left( {x + 2} \right)}}\)\( = \dfrac{{\sin 3}}{{60}}\). Suy ra x = 3 không là TCĐ của đồ thị hàm số. Vậy đồ thị hàm số đã cho không có TCĐ. Đáp án B. Câu hỏi 26 : Tồn tại bao nhiêu giá trị nguyên của tham số \(m\) trong đoạn \(\left[ -2017;2017 \right]\) sao cho đồ thị hàm số \(y=\frac{x-2}{\left( {{x}^{2}}-4mx+4 \right)\left( m{{x}^{2}}-2x+4 \right)}\) có đúng một đường tiệm cận.
Đáp án: A Phương pháp giải: - Tìm tiệm cận ngang của đồ thị hàm số. - Điều kiện để đồ thị hàm số chỉ có duy nhất 1 tiệm cận là nó không có tiệm cận đứng, hay mẫu thức vô nghiệm hoặc có 1 nghiệm duy nhất là nghiệm đơn \(x=2\). Lời giải chi tiết: Dễ thấy \(\underset{x\to \pm \infty }{\mathop{\lim }}\,y=\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{x-2}{\left( {{x}^{2}}-4mx+4 \right)\left( m{{x}^{2}}-2x+4 \right)}=0\) nên \(y=0\) là đường tiệm cận ngang của đồ thị hàm số. Do đó để đồ thị hàm số chỉ có 1 đường tiệm cận thì nó không có tiệm cận đứng. Khi đó phương trình \(\left( {{x}^{2}}-4mx+4 \right)\left( m{{x}^{2}}-2x+4 \right)=0\) vô nghiệm hoặc có nghiệm duy nhất \(x=2\) (nghiệm đơn). Trường hợp 1: Phương trình \(\left( {{x}^{2}}-4mx+4 \right)\left( m{{x}^{2}}-2x+4 \right)=0\) vô nghiệm. \(\Leftrightarrow \) cả hai phương trình \({{x}^{2}}-4mx+4=0\) và \(m{{x}^{2}}-2x+4=0\) đều vô nghiệm. +) Phương trình \({{x}^{2}}-4mx+4=0\) vô nghiệm \(\Leftrightarrow {{\Delta }_{1}}'=4{{m}^{2}}-4<0\Leftrightarrow -1<m<1\). +) Phương trình \(m{{x}^{2}}-2x+4=0\) vô nghiệm \(\Leftrightarrow {{\Delta }_{2}}'=1-4m<0\Leftrightarrow m>\frac{1}{4}\). Kết hợp hai điều kiện trên ta được \(\frac{1}{4}<m<1\). Do đó trong trường hợp này không có số nguyên nào thỏa mãn. Trường hợp 2: Phương trình \(\left( {{x}^{2}}-4mx+4 \right)\left( m{{x}^{2}}-2x+4 \right)=0\) có 1 nghiệm duy nhất là nghiệm đơn \(x=2\). Với \(x=2\) thì \(\left( {{2}^{2}}-4m.2+4 \right)\left( m{{.2}^{2}}-2.2+4 \right)=0\Leftrightarrow \left( 8-8m \right).4m=0\Leftrightarrow \left[ \begin{align} & m=0 \\ & m=1 \\ \end{align} \right.\). +) Nếu \(m=0\) thì \(y=\frac{x-2}{\left( {{x}^{2}}+4 \right)\left( -2x+4 \right)}=-\frac{1}{2\left( {{x}^{2}}+4 \right)}\) nên đồ thị hàm số không có tiệm cận đứng và chỉ có 1 tiệm cận duy nhất (thỏa mãn). +) Nếu \(m=1\) thì \(y=\frac{x-2}{\left( {{x}^{2}}-4x+4 \right)\left( {{x}^{2}}-2x+4 \right)}=-\frac{1}{\left( x-2 \right)\left( {{x}^{2}}+4 \right)}\) nên đồ thị hàm số có 1 tiệm cận đứng \(x=2\) và một tiệm cận ngang \(y=0\) (loại). Vậy \(m=0\) và có 1 giá trị nguyên duy nhất của \(m\) thỏa bài toán. Chọn A.
Câu hỏi 27 : Cho (C) là đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\). Tìm các điểm trên (C) sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất:
Đáp án: B Phương pháp giải: +) Tìm các đường tiệm cận của đồ thị hàm số. +) Gọi \(M(x_0; \,y_0)\) là điểm bất kì thuộc đồ thị hàm số. +) Dựa vào công thức tính khoảng cách từ một điểm đến một đường thẳng để tính khoảng cách từ điểm \(M\) đến từng đường tiệm cận. +) Áp dụng bất đẳng thức Cô-si để tìm \(m\) thỏa mãn đề bài. Lời giải chi tiết: Gọi \(M\left( {m;\dfrac{{m + 1}}{{m - 2}}} \right) \in \left( C \right)\,\left( {m \ne 2} \right)\). Tổng khoảng cách từ M đến 2 đường tiệm cận x = 2 và y = 1 là \(S = \left| {m - 2} \right| + \left| {\dfrac{{m + 1}}{{m - 2}} - 1} \right| = \left| {m - 2} \right| + \dfrac{3}{{\left| {m - 2} \right|}} \ge 2\sqrt {\left| {m - 2} \right|.\dfrac{3}{{\left| {m - 2} \right|}}} = 2\sqrt 3 \) Dấu “=” xảy ra \( \Leftrightarrow \left| {m - 2} \right| = \dfrac{3}{{\left| {m - 2} \right|}} \Leftrightarrow \left| {m - 2} \right| = \sqrt 3 \Leftrightarrow m = 2 \pm \sqrt 3 \) Vậy có 2 điểm thỏa mãn bài toán là \({M_1}\left( {2 + \sqrt 3 ;1 + \sqrt 3 } \right),{M_2}\left( {2 - \sqrt 3 ;1 - \sqrt 3 } \right)\) Chọn B. Câu hỏi 28 : Đồ thị hàm số nào sau đây không có đường tiệm cận?
Đáp án: B Phương pháp giải: Đường thẳng \(x=a\) được gọi là TCĐ của đồ thị hàm số \(y=f(x) \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \pm \infty .\) Hay \(x=a\) là nghiệm của mẫu số và không là nghiệm của tử số. Đường thẳng \(y=b\) được gọi là TCN của đồ thị hàm số \(y=f(x) \Leftrightarrow \mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b .\) Lời giải chi tiết: Các đồ thị của hàm số phân thức luôn có ít nhất một đường tiệm cận. Chỉ có đáp án B là hàm số không có đường tiệm cận. Chọn B. Câu hỏi 29 : Cho hai hàm số \(y = \dfrac{{2x - 1}}{{{m^2} - 8 - x}}\) và \(y = \dfrac{{5 - 2x}}{{x + 4}}\). Tập hợp các giá trị của tham số \(m\) để hai đường tiệm cận đứng của hai đồ thị hàm số trên trùng nhau là:
Đáp án: A Phương pháp giải: Tìm TCĐ của đồ thị hàm số \(y = \frac{{5 - 2x}}{{x + 4}}.\) Tìm TCĐ của đồ thị hàm số \(y = \frac{{2x - 1}}{{{m^2} - 8 - x}}\) theo \(m.\) Sau đó cho hai giá trị đó bằng nhau để tìm \(m.\) Lời giải chi tiết: Xét đồ thị hàm số \(y = \dfrac{{5 - 2x}}{{x + 4}}\) có TCĐ là \(x = - 4\). Suy ra hai đồ thị hàm số đã cho có tiệm cận đứng trùng nhau \( \Leftrightarrow x = - 4\) là TCĐ của đồ thị hàm số \(y = \dfrac{{2x - 1}}{{{m^2} - 8 - x}}\). Ta thấy \(x = - 4\) không là nghiệm của tử số \( \Rightarrow x = - 4\) là TCĐ của đồ thị hàm số\( \Leftrightarrow {m^2} - 8 = - 4 \Leftrightarrow {m^2} - 8 + 4 = 0\)\( \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\). Chọn A. Câu hỏi 30 : Gọi \(a;\,b;\,c\) lần lượt là số các đường tiệm cận của đồ thị hàm số sau: \(y = \dfrac{{1 - 2x}}{{x - 4}};\)\(y = \dfrac{{ - x - 2}}{{{x^2} - 3}}\) và \(y = \dfrac{{25}}{{2{x^2} - 3x + 4}}\). Bất đẳng thức nào sau đây đúng?
Đáp án: C Phương pháp giải: Đường thẳng \(x=a\) được gọi là TCĐ của đồ thị hàm số \(y=f(x) \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \pm \infty .\) Hay \(x=a\) là nghiệm của mẫu số và không là nghiệm của tử số. Đường thẳng \(y=b\) được gọi là TCN của đồ thị hàm số \(y=f(x) \Leftrightarrow \mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b .\) Lời giải chi tiết: +) Xét đồ thị hàm số \(y = \dfrac{{1 - 2x}}{{x - 4}}\) ta thấy đồ thị có TCĐ là \(x = 4\) và TCN là \(y = - 2\) \( \Rightarrow a = 2\). +) Xét đồ thị hàm số \(y = \dfrac{{ - x - 2}}{{{x^2} - 3}}\) ta thấy đồ thị có TCĐ là \(x = \pm \sqrt 3 \) và TCN là \(y = 0\)\( \Rightarrow b = 3\). +) Xét đồ thị hàm số \(y = \dfrac{{25}}{{2{x^2} - 3x + 4}}\) ta thấy đồ thị không có TCĐ và có TCN là \(y = 0\) \( \Rightarrow c = 1\). Vậy chọn C.
|