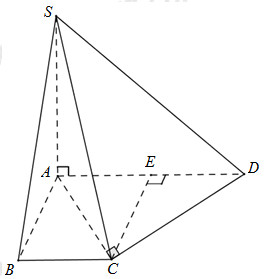
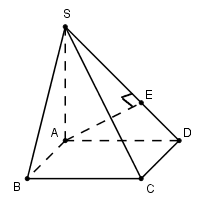
30 bài tập khoảng cách nhận biếtLàm bàiCâu hỏi 1 : Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, \(SA = a;\,\,SA \bot \left( {ABCD} \right);\)\(AB = BC = a\) và \(AD = 2a\). Khoảng cách từ C đến mặt phẳng (SAD) theo a là:
Đáp án: D Phương pháp giải: Xác định khoảng cách từ 1 điểm đến mặt phẳng chứa đường cao. Lời giải chi tiết:
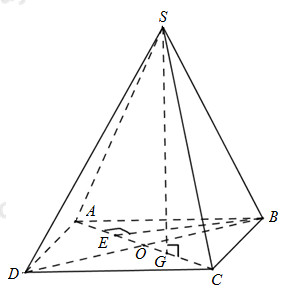
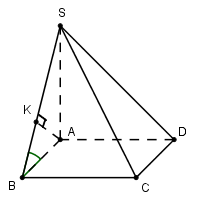
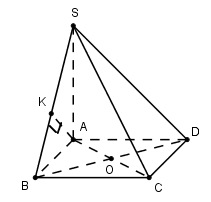
Trong (ABCD) kẻ \(CE \bot AD\) Ta có: \(\left. \begin{array}{l}CE \bot AD\\CE \bot SA\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow CE \bot \left( {SAD} \right) \Rightarrow d\left( {C;\left( {SAD} \right)} \right) = CE\) Tứ giác ABCE là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow CE = AB = a\) Chọn D. Câu hỏi 2 : Cho hình chóp S.ABCD có đáy là hình bình hành với \(AB = 2a,BC = a\sqrt 2 ,BD = a\sqrt 6 \). Hình chiếu vuông góc của S lên (ABCD) là trọng tâm G của tam giác BCD, khoảng cách từ điểm B đến (SAC) theo a là:
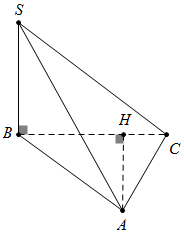
Đáp án: B Phương pháp giải: Lời giải chi tiết:
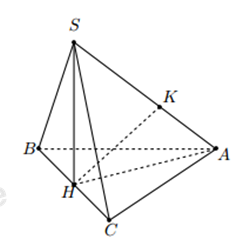
Trong (ABCD) kẻ \(BE \bot AC\) Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}BE \bot AC\\BE \bot SG\,\,\left( {SG \bot \left( {ABCD} \right)} \right)\end{array} \right.\\ \Rightarrow BE \bot \left( {SAC} \right) \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = BE\end{array}\) Ta có: \(B{C^2} + C{D^2} = 2{a^2} + 4{a^2} = 6{a^2} = B{D^2} \Rightarrow \Delta BCD\) vuông tại C\( \Rightarrow ABCD\) là hình chữ nhật (Hình bình hành có 1 góc vuông) Xét tam giác vuông ABC có: \(\dfrac{1}{{B{E^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{B{C^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{2{a^2}}} = \dfrac{3}{{4{a^2}}} \Rightarrow BE = \dfrac{{2a}}{{\sqrt 3 }}\) Chọn B. Câu hỏi 3 : Cho hình chóp S.ABC có đáy ABC là tam giác cạnh \(BC=a,\,\,AC=2a\sqrt{2}\), góc \(\widehat{ACB}={{45}^{0}}\). Cạnh bên SB vuông góc với mặt phẳng (ABC). Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
Đáp án: B Phương pháp giải: Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết:
Từ A kẻ AH vuông góc với \(BC,\,\,H\in BC\) (1) Ta có \(SB\) vuông góc với \(\left( ABC \right)\) \(\Rightarrow SB\bot AH\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\) Từ (1), (2) suy ra \(AH\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AH\). Tam giác AHC vuông tại H, có \(\cos \widehat{HAC}=\dfrac{AH}{AC}\). \(\Rightarrow AH=\cos \widehat{HAC}.AC=\cos {{45}^{0}}.AC=2a\sqrt{2}.\dfrac{\sqrt{2}}{2}=2a\). Chọn B. Câu hỏi 4 : Cho hình chóp S.ABCDcó đáy ABCDlà hình chữ nhật có \(AB=a\sqrt{2}\). Cạnh bên \(SA=2a\) và vuông góc với mặt đáy \(\left( ABCD \right)\). Tính khoảng cách D từ Dđến mặt phẳng \(\left( SBC \right)\)
Đáp án: C Phương pháp giải: Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết:
Do AD // BC nên \(d\left( D;\left( SBC \right) \right)=d\left( A;\left( SBC \right) \right).\) Gọi K là hình chiếu của A trên SB, suy ra \(AK\bot SB\,\,\,\left( 1 \right)\). Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\) Từ (1) và (2) \(\Rightarrow AK\bot \left( SBC \right)\) Khi \(d\left( A;\left( SBC \right) \right)=AK=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{2a\sqrt{3}}{3}.\) Chọn C. Câu hỏi 5 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\) cạnh \(a\). Cạnh bên \(SA=a\sqrt{2}\) và vuông góc với đáy \(\left( ABCD \right)\). Tính khoảng cách \(d\) từ điểm \(B\) đến mặt phẳng \(\left( SCD \right).\)
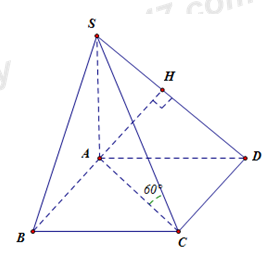
Đáp án: B Phương pháp giải: Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết: Do AB // CD nên \(d\left( B;\left( SCD \right) \right)=d\left( A;\left( SCD \right) \right)\). Kẻ \(AE\bot SD\) tại \(E\). (1) Ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AE\,\,\,\left( 2 \right)\) Từ (1) và (2) \(\Rightarrow AE\bot \left( SCD \right)\). Khi đó \(d\left( A;\left( SCD \right) \right)=AE.\) Tam giác vuông \(SAD,\) có \(AE=\frac{SA.AD}{\sqrt{S{{A}^{2}}+A{{D}^{2}}}}=\frac{a\sqrt{6}}{3}.\) Vậy \(d\left( B;\left( SCD \right) \right)=AE=\frac{a\sqrt{6}}{3}.\) Chọn B. Câu hỏi 6 : Cho hình chóp \(S.ABCD\) có đáy ABCDlà hình vuông cạnh bằng \(a\). Cạnh bên \(SA\) vuông góc với đáy, \(SB\) hợp với mặt đáy một góc \(60{}^\circ \). Tính khoảng cách Dtừ điểm \(D\) đến mặt phẳng \(\left( SBC \right)\).
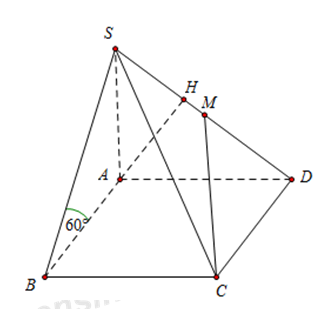
Đáp án: A Phương pháp giải: Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết: Xác định \({{60}^{0}}=\widehat{\left( SB;\left( ABCD \right) \right)}=\widehat{\left( SB;AB \right)}=\widehat{SBA}\Rightarrow SA=AB.\tan \widehat{SBA}=a\sqrt{3}\). Ta có \(AD\parallel BC\Rightarrow AD\parallel \left( SBC \right)\Rightarrow d\left( D;\left( SBC \right) \right)=d\left( A,\left( SBC \right) \right)\) Kẻ \(AK\bot SB\,\,\,\,\left( 1 \right)\). Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\) Từ (1) và (2) \(\Rightarrow AK\bot \left( SBC \right)\) Khi đó \(d\left( A;\left( SBC \right) \right)=AK=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{a\sqrt{3}}{2}.\) Vậy \(d\left( D;\left( SBC \right) \right)=AK=\frac{a\sqrt{3}}{2}.\) Chọn A. Câu hỏi 7 : Cho hình chóp S.ABCDcó đáy ABCDlà hình vuông tâm O, cạnh aCạnh bên \(SA=\frac{a\sqrt{15}}{2}\) và vuông góc với mặt đáy \(\left( ABCD \right).\) Tính khoảng cách Dtừ O đến mặt phẳng \(\left( SBC \right).\)
Đáp án: C Phương pháp giải: Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết:
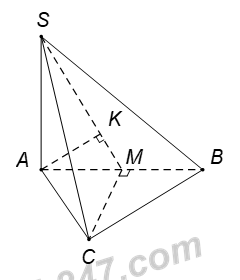
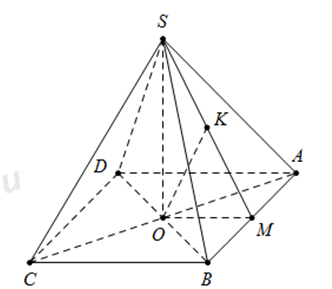
Ta có : \(OA\cap \left( SBC \right)=C\Rightarrow \frac{d\left( O;\left( SBC \right) \right)}{d\left( A;\left( SBC \right) \right)}=\frac{OC}{AC}=\frac{1}{2}\) Do đó \(d\left( O;\left( SBC \right) \right)=\frac{1}{2}d\left( A;\left( SBC \right) \right).\) Gọi \(K\) là hình chiếu của \(A\) trên \(SB\) \(\Rightarrow \)\(AK\bot SB\,\,\,\left( 1 \right)\). Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\) Từ (1) và (2) \(\Rightarrow AK\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AK\) Tam giác vuông SAB, có \(AK=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{a\sqrt{285}}{19}.\) Vậy \(d\left( O;\left( SBC \right) \right)=\frac{1}{2}AK=\frac{a\sqrt{285}}{38}.\) Chọn C. Câu hỏi 8 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA\) vuông góc với mặt phẳng \(\left( ABC \right)\); góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( ABC \right)\) bằng \({{60}^{0}}\). Gọi \(M\) là trung điểm của cạnh \(AB\). Tính khoảng cách Dtừ \(B\) đến mặt phẳng \(\left( SMC \right)\).
Đáp án: B Phương pháp giải: Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết:
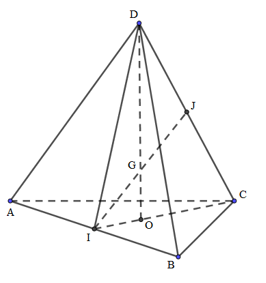
\({{60}^{0}}=\widehat{\left( SB;\left( ABC \right) \right)}=\widehat{\left( SB;AB \right)}=\widehat{SBA};\,\,SA=AB.\tan \widehat{SBA}=a.\sqrt{3}=a\sqrt{3}\). Do M là trung điểm của cạnh AB nên \(d\left( B;\left( SMC \right) \right)=d\left( A;\left( SMC \right) \right)\). Trong (SAB) kẻ \(AK\bot SM\,\,\,\left( 1 \right)\). Ta có : \(\left\{ \begin{array}{l}CM \bot AB\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAB} \right) \Rightarrow CM \bot AK\,\,\,\,\left( 2 \right)\) Từ (1) và (2) \(\Rightarrow AK\bot \left( SCM \right)\Rightarrow d\left( A;\left( SMC \right) \right)=AK.\) Tam giác vuông \(SAM\), có \(AK=\frac{SA.AM}{\sqrt{S{{A}^{2}}+A{{M}^{2}}}}=\frac{a\sqrt{39}}{13}\). Vậy \(d\left( B;\left( SMC \right) \right)=AK=\frac{a\sqrt{39}}{13}\). Chọn B. Câu hỏi 9 : Cho tứ diện đều ABCD có cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD.
Đáp án: B Phương pháp giải: - Khoảng cách giữa hai đường thẳng bằng độ dài đoạn vuông góc chung. Lời giải chi tiết:
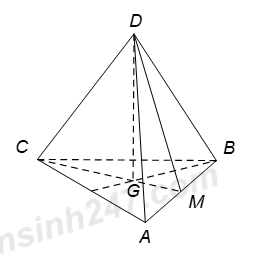
Gọi I, J lần lượt là trung điểm của AB, CD; O là trọng tâm của ABC, G là giao điểm của DO và IJ. * Chứng minh IJ là đoạn vuông góc chung của AB và CD: Các tam giác ABC, ABD đều và bằng nhau, suy ra các đường cao tương ứng \(DI=IC\). \(\Rightarrow \Delta DIC\)cân tại I Mà IJ là trung tuyến \(\Rightarrow IJ\bot CD\) (1) Ta có: \(IC\bot AB\) (vì tam giác ABC đều), \(DO\bot AB\,\)(vì \(DO\bot (ABC)\) \(\Rightarrow AB\bot (DIC)\Rightarrow AB\bot IJ\) (2) Từ (1), (2) suy ra IJ là đoạn vuông góc chung của AB và CD \(\Rightarrow d(AB,\,CD)=IJ\) * Tính IJ: Tam giác ABC đều, cạnh a \(\Rightarrow IC=\frac{a\sqrt{3}}{2}\) J là trung điểm CD \(\Rightarrow JC=\frac{a}{2}\) Tam giác IJC vuông tại J \(\Rightarrow I{{C}^{2}}=I{{J}^{2}}+J{{C}^{2}}\Leftrightarrow {{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}=I{{J}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}\Rightarrow IJ=\frac{a\sqrt{2}}{2}\) Vậy khoảng cách giữa hai đường thẳng AB và CD là \(\frac{a\sqrt{2}}{2}\). Chọn: B. Câu hỏi 10 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông với \(AC=\frac{a\sqrt{2}}{2}\). Cạnh bên SA vuông góc với đáy, SB hợp với đáy góc \({{60}^{0}}\). Tính khoảng cách d giữa hai đường thẳng AD và SC.
Đáp án: A Phương pháp giải: Dựa vào cách xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng còn lại, đưa về dạng toán tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết:
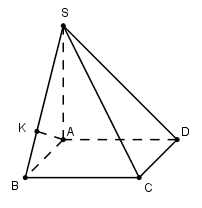
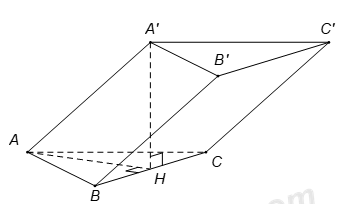
Ta có \(SA\bot \left( ABCD \right)\Rightarrow \widehat{\left( SB;\left( ABCD \right) \right)}=\widehat{\left( SB;AB \right)}=\widehat{SBA}={{60}^{0}}\) Tam giác ABC vuông cân tại B nên \(AB=BC=\frac{AC}{\sqrt{2}}=\frac{a}{2}\) Xét tam giác vuông SAB có : \(SA=AB.\tan {{60}^{0}}=\frac{a}{2}.\sqrt{3}=\frac{a\sqrt{3}}{2}\) Ta có \(d\left( AD;SC \right)=d\left( AD;\left( SBC \right) \right)=d\left( A;\left( SBC \right) \right)\). Kẻ \(AK\bot SB\). Khi đó \(d\left( A;\left( SBC \right) \right)=AK=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{\frac{a\sqrt{3}}{2}.\frac{a}{2}}{\sqrt{{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}}=\frac{a\sqrt{3}}{4}\) Chọn A. Câu hỏi 11 : Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh có độ dài bằng 2a. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với trung điểm H của BC. Tính khoảng cách d giữa hai đường thẳng BB’ và A’H.
Đáp án: B Phương pháp giải: Dựa vào cách xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng còn lại, đưa về dạng toán tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết:
Do \(BB'\parallel AA'\) nên \(d\left( BB';A'H \right)=d\left( BB';\left( AA'H \right) \right)=d\left( B;\left( AA'H \right) \right)\). Ta có \(\left\{ \begin{array}{l}BH \bot AH\\BH \bot A'H\end{array} \right. \Rightarrow BH \bot \left( {AA'H} \right)\) Nên \(d\left( B;\left( AA'H \right) \right)=BH=\frac{BC}{2}=a.\) Vậy khoảng cách \(d\left( BB';A'H \right)=a\). Chọn B. Câu hỏi 12 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy. Biết rằng đường thẳng SC tạo với đáy một góc \({{60}^{0}}.\) Khoảng cách giữa hai đường thẳng AB và SD là
Đáp án: A Phương pháp giải: Dựa vào cách xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng còn lại, đưa về dạng toán tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết:
Ta có \(AC=a\sqrt{2}.\) Do \(SA\bot \left( ABCD \right)\) và \(SC\) tạo với đáy góc \({{60}^{0}}\) nên \(\widehat{SCA}={{60}^{0}}\). Khi đó \(SA=AC\tan {{60}^{0}}=a\sqrt{6}\). Do \(\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)\). Trong (SAD) dựng \(AH\bot SD\,\,\left( 1 \right)\) suy ra \(AB\bot AH\,\,\left( 2 \right)\) là đoạn vuông góc chung \(AB\) và \(SD\). Ta có \(AH=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{a\sqrt{6}.a}{\sqrt{6{{a}^{2}}+{{a}^{2}}}}=\frac{a\sqrt{42}}{7}\). Vậy khoảng cách \(d\left( AB;SD \right)=\frac{a\sqrt{42}}{7}.\) Chọn A. Câu hỏi 13 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng SA và BC.
Đáp án: B Phương pháp giải: Dựa vào cách xác định mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng còn lại. Lời giải chi tiết:
Gọi H là trung điểm của BC khi đó \(SH\bot BC\). Mặt khác \(\left( SBC \right)\bot \left( ABC \right)\) do đó \(SH\bot \left( ABC \right)\). Ta có \(SH=\frac{a\sqrt{3}}{2}\) và \(AB=AC=\frac{a}{\sqrt{2}};AH=\frac{BC}{2}=\frac{a}{2}\). Do \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHA} \right)\). Dựng \(HK\bot SA\) khi đó \(HK\) là đoạn vuông góc chung của \(BC\) và \(SA\). Lại có \(HK=\frac{SH.AH}{\sqrt{S{{H}^{2}}+H{{A}^{2}}}}=\frac{a\sqrt{3}}{4}\). Vậy \(d\left( SA;BC \right)=\frac{a\sqrt{3}}{4}.\) Chọn B. Câu hỏi 14 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết mặt phẳng (SBC) tạo với đáy một góc \({{60}^{0}}\) và M là trung điểm của SD. Tính khoảng cách d giữa hai đường thẳng AB và CM.
Đáp án: B Phương pháp giải: Dựa vào cách xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng còn lại, đưa về dạng toán tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \widehat {SBA}\) là góc giữa 2 mặt phẳng \(\left( SBC \right)\) và \(\left( ABC \right)\) Ta có \(SA=AB\tan \widehat{SBA}=a\sqrt{3}\). Do \(AB||CD\)do đó \(d\left( AB;CM \right)=d\left( AB;\left( CMD \right) \right)=d\left( A;\left( SCD\right) \right)\) Dựng \(AH\bot SD\,\,\,\left( 1 \right)\) ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\,\,\left( 2 \right)\). Từ (1) và (2) \(\Rightarrow AH\bot \left( SCD \right)\), khi đó \(d\left( A;\left( SCD \right) \right)=AH\) Lại có \(AH=\frac{SA.AD}{\sqrt{S{{A}^{2}}+A{{D}^{2}}}}=\frac{a\sqrt{3}.a}{\sqrt{3{{a}^{2}}+{{a}^{2}}}}=\frac{a\sqrt{3}}{2}\). Do đó \(d=\frac{a\sqrt{3}}{2}\). Chọn B. Câu hỏi 15 : Cho tứ diện đều ABCD. Trong các mệnh đề trên mệnh đề nào là sai? Khoảng cách từ điểm D tới mặt phẳng (ABC) là
Đáp án: D Phương pháp giải: Sử dụng các phương pháp xác định góc – khoảng cách trong không gian Lời giải chi tiết:
Gọi M là trung điểm AB và G là trọng tâm tam giác ABC Do ABCD là tứ diện đều \(\Rightarrow \,DG\bot \left( ABC \right)\). Do đó, khoảng cách \(d\left( D;\left( ABC \right) \right)=DG.\) Và G cũng là hình chiếu của D trên mặt phẳng (ABC). Tam giác ABC đều \(\Rightarrow \,\,G\) tâm đường tròn ngoại tiếp tam giác ABC Chọn D. Câu hỏi 16 : Trong các mệnh đề sau, mệnh đề nào đúng?
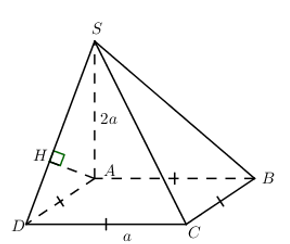
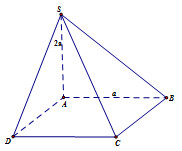
Đáp án: B Phương pháp giải: Sử dụng các phương pháp xác định góc – khoảng cách trong không gian Lời giải chi tiết: Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn nối hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy và ngược lại. Chọn B. Câu hỏi 17 : Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng \(a\sqrt{3}.\) Chiều cao của khối chóp S.ABCD bằng
Đáp án: D Phương pháp giải: Sử dụng các phương pháp xác định góc – khoảng cách trong không gian Lời giải chi tiết:
Gọi O là tâm của hình vuông ABCD. Ta có AB \\ CD \( \Rightarrow \) CD \\ (SAB) \( \Rightarrow \) d(SA,CD) = d(CD,(SAB))= 2d(O,(SAB))= \(a\sqrt 3 \) Gọi M là trung điểm của AB, kẻ \(OK\bot SM\,\,\left( K\in SM \right)\,\,\left( 1 \right)\) ta có : \(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OK\,\,\left( 2 \right)\) Từ (1) và (2) \(\Rightarrow OK\bot \left( SAB \right)\Rightarrow d\left( O;\left( SAB \right) \right)=OK=\frac{a\sqrt{3}}{2}\) Xét tam giác SMO vuông tại , có\(\frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} = \frac{1}{{O{K^2}}} \Rightarrow SO = a\sqrt 3 \) . Chọn D. Câu hỏi 18 : Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) cạnh \(a.\) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {A}'BC \right)\) theo \(a.\)
Đáp án: A Phương pháp giải: Áp dụng phương pháp xác định khoảng cách từ điểm đến mặt phẳng Lời giải chi tiết:
.Gọi H là trung điểm của A’B. Kẻ \(AH\bot {A}'B\,\,\,\left( H\in {A}'B\, \right)\) mà \(BC\bot \left( A{A}'{B}'B \right)\Rightarrow BC\bot AH\Rightarrow \,\,AH\bot \left( {A}'BC \right).\) Tam giác \({A}'AB\) cân tại \(A\,\,\Rightarrow \,\,AH=\frac{{A}'B}{2}=\frac{a\sqrt{2}}{2}.\) Vậy \(d\left( A;\left( {A}'BC \right) \right)=\frac{a\sqrt{2}}{2}.\) Chọn A. Câu hỏi 19 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh A. Cạnh bên \(SA=a\sqrt{3}\) và vuông góc với mặt đáy \(\left( ABC \right)\) Tính khoảng cách \(D\) từ Ađến mặt phẳng \(\left( SBC \right)\).
Đáp án: A Phương pháp giải: Áp dụng phương pháp xác định khoảng cách từ điểm đến mặt phẳng Lời giải chi tiết:
Gọi \(M\) là trung điểm \(BC\), suy ra \(AM\bot BC\) và \(AM=\frac{a\sqrt{3}}{2}\). Gọi \(K\) là hình chiếu của \(A\) trên \(SM\), suy ra \(AK\bot SM\). Ta có \(\left\{ \begin{array}{l}AM \bot BC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot AK.\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(AK\bot \left( SBC \right)\) nên \(d\left[ A,\left( SBC \right) \right]=AK.\) Trong \(\Delta SAM\), có \(AK=\frac{SA.AM}{\sqrt{S{{A}^{2}}+A{{M}^{2}}}}=\frac{3a}{\sqrt{15}}=\frac{a\sqrt{15}}{5}.\) Vậy \(d\left[ A,\left( SBC \right) \right]=AK=\frac{a\sqrt{15}}{5}.\) Chọn A Câu hỏi 20 : Trong các mệnh đề sau, mệnh đề nào sau đây là sai ?
Đáp án: C Phương pháp giải: Lý thuyết xác định khoảng cách giữa hai đường thẳng chéo nhau. Lời giải chi tiết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia. Chọn C Câu hỏi 21 : Hình lập phương ABCD.A’B’C’D’, AB = a. Tính d(A’D’DA; B’C’CB)
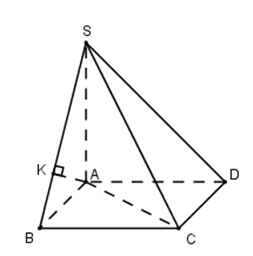
Đáp án: A Phương pháp giải: Lời giải chi tiết: (A’D’DA) // (B’C’CB) * Lấy \(D\in \left( A'D'DA \right)\). Ta có: +) d(A’D’DA; B’C’CB) = d(D; B’C’CB) = DC = a. Chọn đáp án A. Câu hỏi 22 : Chóp S.ABCD, \(SA\bot \left( ABCD \right)\), SA = a, ABCD là hình vuông, AB = a. Tính d(AD; SBC).
Đáp án: D Phương pháp giải: Lời giải chi tiết: * Nhận xét: AD // BC \(\Rightarrow AD\) // (SBC). * Lấy \(A\in AD\). D\). Ta có d(AD; SBC) = d(A; SBC). * Vẽ \(AH\bot SB\overset{Mau\,2}{\mathop{\Rightarrow }}\,AH\bot \left( SBC \right)\). * Chứng minh \(AH\bot \left( SBC \right)\). Do đó d(A; SBC) = AH. * Tính AH: Xét tam giác SAB: \(\frac{1}{A{{H}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{a}^{2}}}\Rightarrow AH=\frac{a}{\sqrt{2}}\) Chọn đáp án D. Câu hỏi 23 : Chóp S.ABC, \(SA\bot \left( ABC \right)\), SA = a. \(\Delta ABC\) đều, AB = a. Tính d(A ; SBC).
Đáp án: B Phương pháp giải: Lời giải chi tiết: * Vẽ \(AE\bot BC,~AH\bot SE\). \(\Rightarrow AH\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AH\). * Chứng minh : \(AH\bot \left( SBC \right)\) (Tự chứng minh). * Tính AH: Ta có: \(AE=\frac{a\sqrt{3}}{2}\) Xét \({{\Delta }_{v}}SAE\): \(\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{E}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{4}{3{{a}^{2}}}=\frac{7}{3{{a}^{2}}}\Rightarrow AH=\frac{a\sqrt{3}}{\sqrt{7}}\). Chọn đáp án B. Câu hỏi 24 : Lăng trụ đứng \(ABC.A'B'C’\), \(\Delta ABC\) vuông ở B, \(AB=a;\,\,BC=2a\). Tính \(d\left( B;\left( ACC'A' \right) \right)\).
Đáp án: C Phương pháp giải: Lời giải chi tiết:
* Vẽ \(\left\{ \begin{align} BH\bot AC \\ BH\bot AA' \\ \end{align} \right.\Rightarrow BH\bot \left( ACC'A' \right)\) \(\Rightarrow d\left( B;\left( ACC'A' \right) \right)=BH\) * Tính BH trong \({{\Delta }_{v}}ABC\) : \(\frac{1}{B{{H}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{4{{a}^{2}}}=\frac{5}{4{{a}^{2}}}\) \(\Rightarrow BH=\frac{2a}{\sqrt{5}}\) Chọn đáp án C. Câu hỏi 25 : Cho hình chóp đều S.ABCD, \(SA=2a;\,\,AB=a\). Tính \(d\left( S;\left( ABCD \right) \right)\).
Đáp án: D Phương pháp giải: Lời giải chi tiết:
* Nối \(AC\cap BD=O\Rightarrow O\) là tâm đáy \(\Rightarrow SO\bot \left( ABCD \right)\). \(\Rightarrow d\left( S;\left( ABCD \right) \right)=SO\). * Tính SO : \(BD=a\sqrt{2}\Rightarrow OB=\frac{a\sqrt{2}}{2}\) \({{\Delta }_{v}}SOB:\,\,SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=\sqrt{4{{a}^{2}}-\frac{2{{a}^{2}}}{4}}=\frac{a\sqrt{14}}{2}\) Chọn đáp án D. Câu hỏi 26 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D’\), \(AA'=a\). Tính \(d\left( A'C';BD \right)\).
Đáp án: C Phương pháp giải: Lời giải chi tiết:
* Nhận xét : \(A'C'\subset \left( A'B'C'D' \right);\,\,BD\subset \left( ABCD \right)\). Mà \(\left( A'B'C'D' \right)//\left( ABCD \right)\) \(\Rightarrow d\left( A'C';BD \right)=d\left( \left( ABCD \right);\left( A'B'C'D' \right) \right)=d\left( A';\left( ABCD \right) \right)=AA'=a\) Chọn đáp án C. Câu hỏi 27 : Chóp S.ABCD, \(SA\bot \left( ABCD \right),\,\,SA=2a,\,\,ABCD\) là hình vuông, \(AB=a\). Tính \(d\left( AB;SD \right)\).
Đáp án: B Phương pháp giải: Lời giải chi tiết:
* Nhận xét : \(\left\{ \begin{align} AB\bot AD \\ AB\bot SA \\ \end{align} \right.\Rightarrow AB\bot \left( SAD \right)\) \(\Rightarrow AB\bot SD\) * Chọn \(A\in AB\). Vẽ \(AH\bot SD\). Vì \(AB\bot \left( SAD \right)\Rightarrow AB\bot AH\) \(d\left( AB;SD \right)=AH\) * Tính AH : \({{\Delta }_{v}}SAD:\,\,\frac{1}{A{{H}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{4{{a}^{2}}}=\frac{5}{4{{a}^{2}}}\Rightarrow AH=\frac{2a}{\sqrt{5}}\) Chọn đáp án B. Câu hỏi 28 : Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\), khoảng cách từ đỉnh \(A\) đến đường thẳng \({B}'D\) bằng
Đáp án: B Phương pháp giải: Dựng đường cao, áp dụng hệ thức lượng trong tam giác vuông tính khoảng cách Lời giải chi tiết: Kẻ \(AH\bot {B}'D\,\,\,\,\,\left( H\in {B}'D \right)\) suy ra \(\frac{1}{A{{H}^{2}}}=\frac{1}{A{{D}^{2}}}+\frac{1}{A{{{{B}'}}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{2{{a}^{2}}}=\frac{3}{2{{a}^{2}}}\Rightarrow \,\,AH=\frac{a\sqrt{6}}{3}.\) Chọn B Câu hỏi 29 : Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng chứa đáy \(\left( {ABCD} \right)\), độ dài cạnh \(SA\) bằng \(2a\) (Tham khảo hình vẽ bên). Khoảng cách từ \(S\) đến mặt phẳng \(\left( {ABCD} \right)\) bằng:
Đáp án: B Phương pháp giải: Khoảng cách từ \(S\) đến \(\left( {ABCD} \right)\) bằng độ dài khoảng cách từ \(S\) đến hình chiếu của \(S\) lên \(\left( {ABCD} \right)\). Lời giải chi tiết: \(SA \bot \left( {ABCD} \right) \Rightarrow d\left( {S;\left( {ABCD} \right)} \right) = SA\). Chọn B. Câu hỏi 30 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm thỏa mãn \(f'\left( 8 \right) = 5\). Giá trị của biểu thức \(\mathop {\lim }\limits_{x \to 8} \dfrac{{f\left( x \right) - f\left( 8 \right)}}{{x - 8}}\) bằng:
Đáp án: B Phương pháp giải: Hàm số \(y = f\left( x \right)\) có đạo hàm tại điểm \(x = {x_0}\) khi tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\). Khi đó \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\). Lời giải chi tiết: Do hàm số \(y = f\left( x \right)\) có đạo hàm thỏa mãn \(f'\left( 8 \right) = 5\) nên \(\mathop {\lim }\limits_{x \to 8} \dfrac{{f\left( x \right) - f\left( 8 \right)}}{{x - 8}} = f'\left( 8 \right) = 5\). Chọn B.
|