25 bài tập cơ bản Đồ thị của hàm số y=ax+b (a khác 0)Làm bàiCâu hỏi 1 : “ĐTHS y=ax+b(a≠0)y=ax+b(a≠0) cắt trục hoành tại điểm có hoành độ bằng ….. và cắt trục tung tại điểm có tung độ bằng ……” Trong dấu “…” là gì?
Đáp án: B Phương pháp giải: Phương pháp: - Sử dụng lý thuyết được học: ĐTHS cắt trục hoành, trục tung - So sánh với đề bài để tìm ra biểu thức cần điền vào chỗ trống. Lời giải chi tiết: Cách giải: ĐTHS y=ax+by=ax+b cắt trục hoành ⇒y=0⇒ax+b=0⇔x=−ba⇒y=0⇒ax+b=0⇔x=−ba ĐTHS y=ax+by=ax+b cắt trục tung ⇒x=0⇒y=a.0+b⇒y=b⇒x=0⇒y=a.0+b⇒y=b Chọn B. Câu hỏi 2 : Điểm nào sau đây thuộc ĐTHS y=2x+1y=2x+1:
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức: Điểm (x0;y0)(x0;y0) thuộc ĐTHS y=ax+b⇔ax0+b=y0y=ax+b⇔ax0+b=y0. Lời giải chi tiết: Cách giải: Ta có ax0+b=2.0+1=1=y0⇒(0;1)ax0+b=2.0+1=1=y0⇒(0;1) thuộc ĐTHS đã cho. Chọn A.
Câu hỏi 3 : Với giá trị nào của mm thì điểm (1;2)(1;2) thuộc đường thẳng x−y=mx−y=m?
Đáp án: D Phương pháp giải: Phương pháp: Điểm (x0;y0)(x0;y0)thuộc ĐTHS y=ax+b⇔ax0+b=y0y=ax+b⇔ax0+b=y0. Lời giải chi tiết: Cách giải: Điểm (1;2)(1;2) thuộc ĐTHS x−y=m⇔1−2=m⇔−1=mx−y=m⇔1−2=m⇔−1=m. Chọn D.
Câu hỏi 4 : Điểm nào sau đây thuộc đồ thị hàm số y=2x+1y=2x+1 ?
Đáp án: D Phương pháp giải: Thay các điểm ở từng đáp án vào hàm số. Lời giải chi tiết: Ta có: 2.0+1=1⇒N(0;1)2.0+1=1⇒N(0;1) thuộc đồ thị hàm số y=2x+1y=2x+1. Chọn D. Câu hỏi 5 : Hệ số góc của đường thẳng (d):y=−2x+3(d):y=−2x+3 là:
Đáp án: A Phương pháp giải: Đường thẳng y=ax+by=ax+b có hệ số góc là a.a. Lời giải chi tiết: Ta có: đường thẳng y=−2x+3y=−2x+3 có hệ số góc là a=−2.a=−2. Chọn A. Câu hỏi 6 : Đồ thị hàm số y=2x−1y=2x−1 đi qua điểm
Đáp án: B Phương pháp giải: Thay tọa độ các điểm vào công thức hàm số và chọn đáp án đúng. Lời giải chi tiết: Thay x=2x=2 vào hàm số y=2x−1⇒2.2−1=3=yy=2x−1⇒2.2−1=3=y Vậy N(2;3)N(2;3) thuộc đồ thị hàm số. Chọn B. Câu hỏi 7 : Giá trị của mm để đường thẳng y=(m−1)x−my=(m−1)x−m cắt trục tung tại điểm có tung độ là 1+√21+√2 là:
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức ĐTHS bậc nhất cắt trục Oy tại điểm (0;b) và tính toán. Lời giải chi tiết: Cách giải: ĐTHS y=(m−1)x−m cắt trục tung tại điểm có tung độ là 1+√2 ⇒−m=1+√2⇒m=−1−√2 Chọn A. Câu hỏi 8 : Điểm (−2;3) thuộc đường thẳng nào trong các đường thẳng có phương trình sau:
Đáp án: C Phương pháp giải: Phương pháp: - Điểm (x0;y0) thuộc ĐTHS y=ax+b⇔ax0+b=y0. - Tính toán và chọn đáp án phù hợp. Lời giải chi tiết: Cách giải: Ta có 3(−2)−2.3=−12≠3=> loại A 3(−2)−3=−9≠0 => loại B 0(−2)+3=3 Chọn C. Câu hỏi 9 : ĐTHS y=12x−3và y=−x+3cắt nhau tại điểm :
Đáp án: D Phương pháp giải: Phương pháp: Sử dụng kiến thức: 2 đường thẳng cắt nhau: Xét phương trình hoành độ giao điểm 2 đường thẳng rồi tính toán. Lời giải chi tiết: Cách giải: Xét phương trình hoành độ giao điểm: 12x−3=−x+3⇔32x=6⇔x=4⇒y=−4+3=−1. Chọn D. Câu hỏi 10 : ĐTHS y=(3−m)x+m+3 đi qua gốc tọa độ khi:
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức: Điểm thuộc đồ thị hàm số. Lời giải chi tiết: Cách giải: Ta có điểm O(0 ;0) thuộc đường thẳng y=(3−m)x+m+3⇔m+3=0⇔m=−3 Chọn A. Câu hỏi 11 :
Tìm giá trị của m để đồ thị của hàm số y=(m−2017)x+2018 đi qua điểm (1;1) ta được
Đáp án: B Phương pháp giải: Thay tọa độ của điểm (1;1) vào hàm số y=(m−2017)x+2018 để tìm giá trị của m. Lời giải chi tiết: Đồ thị của hàm số y=(m−2017)x+2018 đi qua điểm (1;1) nên ta có: 1=(m−2017).1+2018⇒1=m−2017+2018⇒m=0 Vậy để đồ thị của hàm số y=(m−2017)x+2018 đi qua điểm (1;1) thì m=0. Chọn B. Câu hỏi 12 : Trong các hàm số dưới đây, hàm số bậc nhất có đồ thị đi qua điểm A(1;4)là:
Đáp án: C Phương pháp giải: Thay giá trị A(1;4) vào lần lượt các đáp án Lời giải chi tiết: +) Theo đầu bài hàm số cần tìm là hàm số bậc nhất, nên A.y=x2+3 là hàm số bậc 2 nên loại +) Lần lượt thay x=1 vào các hàm số: −)y=x−3=1−3=−2−)y=4x=4.1=4−)y=4−x=4−1=3 Như vậy ta thấy điểm A(1,4) thuộc đồ thị hàm số y=4x Chọn đáp án C. Câu hỏi 13 : Tìm a;b để đồ thị hàm số y=ax+b thỏa mãn : Câu 1: Đi qua M(1;2) và song song với đường thẳng y=x−2.
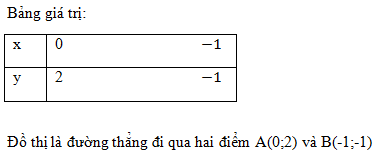
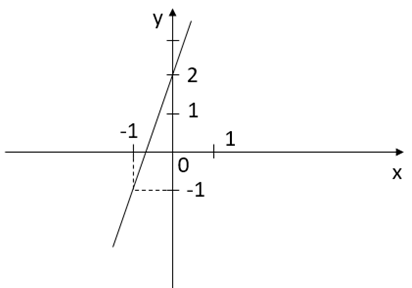
Đáp án: A Phương pháp giải: Đường thẳng y=ax+b song song với đường thẳng y=a′x+b′ khi và chỉ khi {a=a′b≠b′ Đường thẳng y=ax+b đi qua M(x0;y0) khi y0=ax0+b Lời giải chi tiết: Đường thẳng y=ax+b(d) song song với đường thẳng y=x−2⇒a=1⇒y=x+b (d) đi qua M(1;2)⇒2=1+b⇒b=1 Vậy hàm số cần tìm y=x+1 Câu 2: Đi qua 2 điểm M(1;2) và N(−1;0)
Đáp án: B Phương pháp giải: Đường thẳng y=ax+b đi qua M(x0;y0) khi y0=ax0+b Lời giải chi tiết: Đường thẳng y=ax+b đi qua 2 điểm M(1;2) và N(−1;0) suy ra ta có: {2=a+b0=−a+b⇒a=b=1 Vậy hàm số y=x+1 Câu hỏi 14 : Nếu đồ thị hàm số y=12x−b cắt trục hoành tại điểm có hoành độ bằng 2 thì giá trị của b là:
Đáp án: D Phương pháp giải: Thay điểm đi qua vào hàm số. Lời giải chi tiết: Hàm số y=12x−b cắt trục hoành tại điểm có hoành độ bằng 2 ⇒(2;0) thuộc đồ thị hàm số. Khi đó ta có: 0=12.2−b⇔b=1. Vậy b=1. Chọn D. Câu hỏi 15 : Cho đường thẳng d:y=x−1. Khi đó khoảng cách từ gốc tọa độ đến đường thẳng đã cho là:
Đáp án: C Phương pháp giải: Phương pháp: - Tìm giao điểm của đường thẳng với trục hoành, trục tung - Dựng hình chiếu của tam giác được tạo thành - Áp dụng hệ thức trong tam giác để tính khoảng cách từ điểm O đến 1 đường thẳng. - Tính kết quả thu được Lời giải chi tiết: Cách giải: Ta có: d∩Ox=A(1;0)⇒OA=1d∩Oy=B(0;−1)⇒OB=1 Ta có OA⊥OB. Gọi H là hình chiếu của O trên đường thẳng AB. Áp dụng hệ thức trong tam giác ta có: 1OH2=1OA2+1OB2=11+11=2⇒OH=√22 Chọn C.
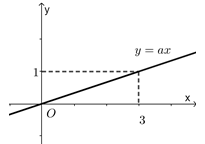
Câu hỏi 16 : Cho hàm số y=ax có đồ thị như hình bên. Giá trị của a bằng:
Đáp án: C Phương pháp giải: Thay tọa độ điểm thuộc đồ thị vào hàm số để tìm hệ số a Lời giải chi tiết: Ta thấy M(3;1) thuộc đồ thị hàm số nên 1=a.3⇔a=13 Chọn C. Câu hỏi 17 : Trong các hàm số sau, đồ thị hàm số nào là đường thẳng tạo với trục hoành một góc 450.
Đáp án: C Phương pháp giải: Gọi α là góc tạo bởi đường thẳng d:y=ax+b(a≠0) với trục hoành. Ta có: tanα=a⇒α là góc nhọn nếu a>0,α là góc tù nếu a<0. Lời giải chi tiết: Đường thẳng tạo với trục hoành góc 450⇒tanα=1. Chọn C Câu hỏi 18 : Giá trị của tham số m để đường thẳng y=(2m+1)x+3 đi qua điểm A(−1;0) là:
Đáp án: D Phương pháp giải: Đường thẳng d:y=ax+b đi qua điểm M(x0;y0)⇔y0=ax0+b. Lời giải chi tiết: Đường thẳng y=(2m+1)x+3 đi qua điểm A(−1;0) ⇔0=(2m+1).(−1)+3⇔2m+1=3⇔m=1. Chọn D. Câu hỏi 19 : Cho điểm M(xM;yM) thuộc đồ thị hàm số y=−3x2. Biết xM=−2. Tính yM.
Đáp án: C Phương pháp giải: Điểm M(x0;y0) thuộc đồ thị hàm số y=ax2(a≠0)⇒y0=ax20. Lời giải chi tiết: Điểm M(xM;yM) có hoành độ xM=−2 và thuộc đồ thị hàm số y=−3x2 ⇒yM=−3.(−2)2=−12. Chọn C. Câu hỏi 20 : Điểm nào dưới đây thuộc đường thẳng y=3x−5?
Đáp án: B Phương pháp giải: Đường thẳng d:y=ax+b đi qua điểm M(x0;y0)⇔y0=ax0+b. Lời giải chi tiết: +) Xét điểm M(3;−5) ta có: 3.3−5=4≠−5⇒M∉d:y=3x−5. +) Xét điểm N(1;−2) ta có: 3.1−5=−2⇒N∈d:y=3x−5. Chọn B. Câu hỏi 21 : Cho hàm số f(x)=2x+5;g(x)=2x2−1 Câu 1: So sánh f2(3) và g(2)
Đáp án: D Phương pháp giải: Để tính f(x0) thay x=x0vào biểu thức f(x) Lời giải chi tiết: Ta có f(x)=2x+5⇒f(3)=3.2+5=11⇒f2(3)=121 g(x)=2x2−1⇒g(2)=2.22−1=7⇒f2(3)>g(2) Câu 2: Tìm x để g(x)=f(x).
Đáp án: A Phương pháp giải: Giải phương trình f(x)=g(x) Lời giải chi tiết: g(x)=f(x)⇔2x+5=2x2−1⇔2x2−2x−6=0⇔x=1±√132 Vậy x=1±√132 Câu hỏi 22 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 23 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 24 : Đường thẳng y=ax+b đi qua điểm (3;2). Khi đó 6a+2b bằng:
Đáp án: B Phương pháp giải: Phương pháp: - Sử dụng kiến thức: điểm thuộc đường thẳng. - Biến đổi biểu thức cần tính thành biểu thức có thể tính được theo biểu thức đã xuất hiện - Tính kết quả thu được Lời giải chi tiết: Cách giải: Điểm (3;2) thuộc đường thẳng y=ax+b⇒3a+b=2 Ta có 6a+2b=2(3a+b)=2.2=4 Chọn B. Câu hỏi 25 : Cho 2 đường thằng d:y=2x−1;d′:y=x−3. Đường thẳng nào đi qua giao điểm của d và d′?
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức: - Xác định giao điểm của 2 đường thẳng - Sử dụng kiến thức điểm thuộc đường thẳng để tìm ra đáp án phù hợp. Lời giải chi tiết: Cách giải: Ta có: 2x−1=x−3⇔x=−2⇒y=−5⇒M(−2;−5) Trước hết xét M có thuộc đường thẳng y=3x+1 không? Ta có 3.xM+1=3.(−2)+1=−5=yM Chọn A.
|