Phương pháp giải:

Dựa vào tính chất của đường trung trực của đoạn thẳng : những điểm nằm trên đường trung trực của đoạn AB sẽ cách đều hai đầu mút của đoạn \(AB\).

Lời giải chi tiết:

Các điểm cách đều \(A, B\) của đoạn \(AB\) là đường trung trực của đoạn \(AB\).

Chọn C

Phương pháp giải:

Dựa vào dấu hiệu nhận biết hình thoi.

Lời giải chi tiết:

Các đáp án A, C, D đều cho ta hình thoi chỉ có đáp án C: Tứ giác có hai đường chéo vuông góc và bằng nhau không cho ta hình thoi.

Chọn B

Phương pháp giải:

Ta dựa vào tính chất của hình thoi.

Lời giải chi tiết:

Theo tính chất của hình thoi ta thấy hai đường chéo của hình thoi không bằng nhau.

Chọn C

Phương pháp giải:

Dựa vào tính chất khoảng cách giữa hai đường thẳng.

Lời giải chi tiết:

Tập hợp tất cả các điểm cách đều đường thẳng \(a\) cố định một khoảng bằng \(2,5\)cm là hai đường thẳng song song với \(a\) và cách \(a\) một khoảng bằng \(2,5\)cm.

Chọn B

Phương pháp giải:

Vẽ thêm \(Ax // DE\). Ta chứng minh \(Ax, DE, BC\) là ba đường thẳng song song cách đều. Từ đó suy ra \(AE = EC\).

Lời giải chi tiết:

Do \(DE // BC\) theo giả thiết nên vẽ thêm \(Ax // DE\) thì \(Ax//DE//BC\).   (1)

Vì \(D\) là trung điểm của \(AB\) nên \(AD = DB\) (2)

Từ (1) và (2) suy ra \(Ax, DE, BC\) là ba đường thẳng song song cách đều nên nó chắn trên đường thẳng \(AC\) hai đoạn liên tiếp bằng nhau \(AE = EC\).(đpcm)

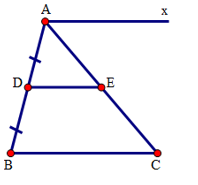
Phương pháp giải:

Dựa vào công thức tính chu vi hình thoi: chu vi hình thoi bằng độ dài cạnh nhân 4, từ đó suy ra độ dài cạnh.

Lời giải chi tiết:

Cạnh của hình thoi là: 16 : 4 = 4cm

Chọn B 

Phương pháp giải:

+ Ta chỉ ra NQ = MP theo thính chất hình thang cân.

+ Chứng minh ABCD là hình thoi theo dấu hiệu tứ giác có 4 cạnh bằng nhau.

Lời giải chi tiết:

Do MNPQ là hình thang cân nên MP = NQ. (hình thang cân có hai đường chéo bằng nhau). 

Do A, D lần lượt là trung điểm của MN, MQ nên AD là đường trung bình của tam giác MNQ. Do đó  \(DA = {1 \over 2}QN\) (1)  (tính chất đường trung bình của tam giác).   (2)

Chứng minh tương tự ta cũng có BC, AB, DC lần lượt là đường trung bình của các tam giác PQN, MNP, QMP.

Do đó \(BC = {1 \over 2}QN;\,\,AB = {1 \over 2}MP;\,\,DC = {1 \over 2}MP\,\,\,\,\left( 3 \right)\)

Từ (1), (2), (3) suy ra AB = BC = CD = DA.

Do đó ABCD là hình thoi.

Chọn D

Phương pháp giải:

Để chứng minh AGCH là hình thoi ta dựa vào dấu hiệu hình bình hành có đường chéo là đường phân giác của một góc là hình thoi. 

Lời giải chi tiết:

Gọi O là giao điểm của AC và BD thì  (do O là giao điểm của hai đường chéo của hình thoi)

Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:

\(AB = AD,\widehat {\,\,B} = \widehat D,\,\,BE = DF.\)

Từ đó suy ra  \(\Delta ABE = \Delta ADF(c.g.c)\)

Suy ra \(\widehat {{A_1}} = \widehat {{A_4}}\) (hai góc tương ứng).

Mà AC là phân giác của \(\widehat A \Rightarrow \widehat {{A_2}} = \widehat {{A_3}}.\)  (1)

Do đó AO là phân giác của  \(\widehat {HAG}.\)

Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.

Suy ra HO = OG.(2)

Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi)   (3)

Từ (1), (2), (3) suy ra AHCG là hình thoi. (đpcm)

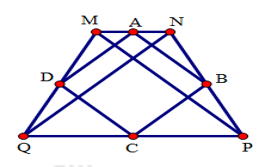
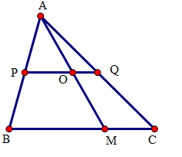
Phương pháp giải:

+ Dựa vào tính chất của hình thoi để suy ra hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.

+ Sử dụng định lý Pytago để tính độ dài cạnh hình thoi.

Lời giải chi tiết:

Giả sử hình thoi ABCD có hai đường chéo AC = 16cm, BD = 12cm cắt nhau tại O.

Theo tính chất hình thoi ta có AC vuông góc với BD, O là trung điểm của AC, BD.

Do đó: \(OA=\frac{1}{2}AC=16:2=8(cm);\,\,\,OB=\frac{1}{2}BD=12:2=6(cm)\)

Áp dụng định lý Pytago cho tam giác ABO vuông tại O ta có:

\(A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}}={{6}^{2}}+{{8}^{2}}=100\Rightarrow AB=10(cm)\)

Vậy độ dài cạnh hình thoi là 10cm.

Chọn D.

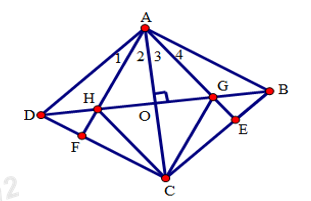
Phương pháp giải:

+ Chứng minh \(PQ\) là đường trung bình của tam giác \(ABC\) để suy ra \(PQ // BC\).

+ Chứng minh \(O\) thuộc \(PQ\)

Lời giải chi tiết:

Gọi \(P, Q\) lần lượt là trung điểm của \(AB, AC\). Suy ra \(PQ\) là đường trung bình của tam giác \(ABC\). Do đó \(PQ // BC\)

Nếu \(M\) trùng với \(B\) thì ta có \(O\) trùng với \(P\)

Nếu \(M\) trùng với \(C\) thì \(O\) trùng với \(Q\).

Do đó nếu \(M\) di chuyển trên \(BC\) thì \(O\) di chuyển trên đường thẳng \(PQ\) song song với cạnh \(BC\), với \(P, Q\) là trung điểm của các cạnh \(AB, AC\)

Chọn D

Phương pháp giải:

+ Tính MC dựa vào định lý Pitago

Lời giải chi tiết:

Gọi \(H, K, I\) lần lượt là chân đường vuông góc kẻ từ \(M\) đến \(AB, AD, DC.\)

Ta có MI = AD  - AK = AD – MH = 6 – 2 = 4

          IC = DC – DI = AB – KM = 10 – 4 = 6

Áp dụng định lý Pitago cho tam giác \(MIC\) ta có:

 \(\begin{array}{l}M{C^2} = M{I^2} + I{C^2} = {4^2} + {6^2} = 52\\\Rightarrow MC = \sqrt {52}\end{array}\)

Chọn D

Phương pháp giải:

+ Vẽ \(OI \bot d\) ta chứng minh \(OI, AE, CG\) là ba đường thẳng song song cách đều để suy ra \(EI = IG\);  \(OI, BF, DH\) là ba đường sog song cách đều để suy ra \(FI = IH\).

+ Chứng minh \(OI\) là đường trung bình của hai hình thang \(AEGC\) và \(BFHD\)

+ Áp dụng định lý đường trung bình của hình thang để suy ra điều phải chứng minh.

Lời giải chi tiết:

Do \(AE, BF, CG, DH\) cùng vuông góc với d suy ra \(AE // BF // CG//DH\). Nên \(AEGC\) và \(BFHD\) là hai hình thang vuông.

Gọi O là giao điểm của hai đường chéo \(AC\) và \(BD\). Áp dụng tính chất về đường chéo vào hình bình hành \(ABCD\), ta được:

\(AO = OC\)    (1), \(BO  = OD\) (2)

Vẽ thêm \(OI \bot d\) thì \(OI // AE // CG\) (3) và \(OI // BF // DH\) (4) (do cùng vuông góc với d).

Từ (1) và (3) suy ra \(OI, AE, CG\) là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng d hai đoạn liên tiếp bằng nhau là \(EI = IG\)   (5)

Từ (2) và (4) suy ra \(OI, BF, DH\) cũng là ba đường thẳng song song cách đều nên chúng cũng chắn trên đường thẳng d hai đoạn liên tiếp bằng nhau là \(FI = IH\)  (6)

Từ (1) với (5) và (2) với (6) ta có \(OI\) là đường trung bình của hai hình vuông \(AEGC\) và \(BFHD\).

Áp dụng định lý đường trung bình vào hai hình thang trên ta được:

\(2OI  = AE + CG = BF + DH\)

Phương pháp giải:

+ Gọi M là trung điểm của BC, ta chứng minh được tam giác MDE cân tại M từ đó suy ra ID = IE

+ Chứng minh BH, MI, CK là ba đường song song cách đều nên IH = IK

+ Từ đó suy ra điều phải chứng minh.

Lời giải chi tiết:

Vì BD, CE là các đường  cao của tam giác ABC nên \(BD \bot AC,CE \bot AB\) do đó tam giác BDC vuông tại D, tam giác CEB vuông tại E.

Gọi M là trung điểm của BC, vẽ DM, EM thì DM, EM là các trung tuyến ứng với cạnh huyền của tam giác BDC và tam giác CEB.

Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào hai tam giác vuông trên, ta được

\(DM = \frac{1}{2}BC,EM = \frac{1}{2}BC\)

Suy ra DM  = EM, suy ra tam giác MDE cân tại M.

Xét tứ giác BHKC có: \(BH \bot DE,KC \bot DE,\widehat {BHK} = {90^0}\) nên tứ giác BHKC là hình thang vuông.

Vẽ thêm \(MI \bot DE\) thì BH // MI // KC(vì cùng vuông góc với DE)   (1)

Mà BM = MC  (2)

Từ (1) và (2) suy ra BH, MI, CK là ba đường thẳng song song cách đều  nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3)

Áp dụng tính chất về đường cao ứng với cạnh đáy vào tam giác cân MDE ta được EI = ID (4)

Trừ theo vế đẳng thức (3) cho (4), ta được EH = DK.(đpcm)

Phương pháp giải:

+ Ta dựa vào tính chất hình thoi để tính độ dài hai cạnh AH, HB

+ Tính độ dài cạnh hình thoi dựa vào định lý Pitago.

Lời giải chi tiết:

Giả sử ABCD là hình thoi có hai đường chéo AC = 10 cm, BD = 24cm.

Do ABCD là hình thoi nên:

\(AC \bot BD;\,\,AH = {1 \over 2}AC = {1 \over 2}.10 = 5\left( {cm} \right);\,\,HB = {1 \over 2}BD = {1 \over 2}.24 = 12\left( {cm} \right).\)

Xét tam giác AHB vuông tại H ta có:   \(A{B^2} = A{H^2} + H{B^2} = {5^2} + {12^2} = 25 + 144 = 169\)

Suy ra AB = 13cm.

Chọn B

Phương pháp giải:

+ Ta dựa vào tính chất hình thoi để suy ra  \(AC \bot BD,\,\,AH = {1 \over 2}AC.\,\)

+ Áp dụng định lý Pitago để tính độ dài HB, từ đó suy ra độ dài BD.

Lời giải chi tiết:

Giả sử ABCD là hình thoi có độ dài cạnh  là 25cm, đường chéo AC = 14 cm.

Theo tính chất hình thoi ta có: \(AC \bot BD,\,\,\,AH = {1 \over 2}AC = 7\left( {cm} \right).\)

Xét tam giác AHB vuông tại H ta có:  \(H{B^2} = A{B^2} - A{H^2} = {25^2} - {7^2} = 576\)

Suy ra  HB = 24(cm)

Do đó  BD = 2.HB = 2.24 = 48(cm).

Chọn B

Phương pháp giải:

+ Ta chứng minh tam giác ADC là tam giác đều từ đó suy ra số đo góc D

+ Ta thấy góc C và góc D là hai góc bù nhau nên ta suy ra số đo góc C.

+ Từ đó suy ra số đo hai góc còn lại.

Lời giải chi tiết:

Gọi H là chân đường cao kẻ từ A đến cạnh CD. Từ giả thiết ta có: \(AH \bot DC,CH = HD\), suy ra AH là đường trung trục của đoạn CD nên AC = CD.      (1)

Do ABCD là hình thoi nên AD = CD (2)

Từ (1) và (2) suy ra AD = CD = AC nên tam giác ACD là tam giác đều, do đó \(\widehat D = {60^0}\)

Vì góc A và góc D là hai góc trong cùng phía của AB // CD nên chúng bù nhau hay \(\widehat A = {180^0} - {60^0} = {120^0}\)

Áp dụng tính chất về góc vào hình thoi ta được: \(\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}\)

Phương pháp giải:

+ Để chứng minh \(MN \bot PQ\) trước hết ta chứng minh MNPQ là hình thoi dựa vào dấu hiệu tứ giác có bốn canh bằng nhau là hình thoi.

+ Ta nhận xét thấy MN, PQ là hai đường chéo của hình thoi nên \(MN \bot PQ\)

Lời giải chi tiết:

Từ giả thiết ta có MN, NP, NQ, QM  lần lượt là các đường trung bình của các tam giác BDE, ECD, DCB, BEC. (định nghĩa đường trung bình).

Đặt BD = CE =2a.

Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:

\(MP = {1 \over 2}BD = a;NQ = {1 \over 2}DB = a;NP = {1 \over 2}CE = a;MQ = {1 \over 2}CE = a\)

Suy ra MN = NP = PQ = QM.

Tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi.

Áp dụng tính chất về đường chéo vào hình thoi MNPQ ta được: \(MN \bot PQ\) (đpcm).

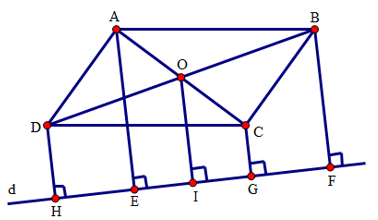
Phương pháp giải:

+ Gọi G, H lần lượt là trung điểm của AC, BD, ta chứng minh EGFH là hình thoi.

+ Dựa vào tính chất đường chéo của hình thoi để suy ra EF là tia phân giác của HFG.

+ Từ đó tính được số đo góc EFC nhờ \(\widehat {GFC} = \widehat {ADC},\widehat {HFG} = \widehat {BCD}\)

Lời giải chi tiết:

Gọi G, H lần lượt là trung điểm của AC, BD.

Vì E, G lần lượt là trung điểm của AB, AC nên EG là đường trung bình của tam giác ABC . Suy ra  \(EG = {1 \over 2}BC;\,\,EG//BC.\)

Chứng minh tương tự ta cũng có:

\(GF = {1 \over 2}AD,FH = {1 \over 2}BC,HE = {1 \over 2}AD;\,\,GF//AD;\,\,FH//BC;\,\,HE//AD.\)

Mà AD = BC (gt), nên EG = GF = FH = HE.

Suy ra tứ giác EGFH là thoi 

Suy ra EF là tia phân giác của góc \(\widehat {HFG} \Rightarrow \widehat {EFG} = {1 \over 2}\widehat {HFG}.\)

\(\widehat {GFC} = \widehat {ADC} = {80^0}\,\left( {do\,\,GF//AD} \right);\,\,\widehat {HFD} = \widehat {BCD} = {50^0}\,\,\,\left( {do\,\,\,FH//BC} \right).\)

Do đó  \(\widehat {HFG} = {180^0} - \left( {\widehat {GFC} + \widehat {HFD}} \right) = {50^0} \Rightarrow \widehat {EFG} = {1 \over 2}{.50^0} = {25^0}\)

Vậy \(\widehat {EFC} = \widehat {EFG} + \widehat {GFC} = {25^0} + {80^0} = {105^0}\)

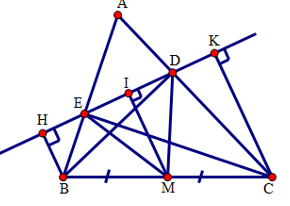
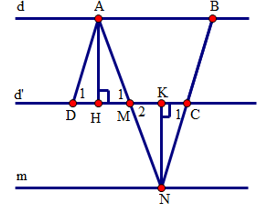
Phương pháp giải:

Vẽ ba vị trí của C, D, dự đoán rằng N di chuyển trên đường thẳng song song với d và d’.

Vẽ \(NK \bot d',K \in d'\). Cần chứng minh NK không đổi.

Vẽ \(AH \bot d',H \in d'\)

Ta chứng minh được \(\Delta AMD = \Delta NMC \Rightarrow AM = NM\)

                                   \(\Delta HAM = \Delta KNM \Rightarrow AH = NK\)

Lời giải chi tiết:

\(NK \bot d',AH \bot d\left( {K \in d',H \in d} \right)\).

Xét \(\Delta AMD\) và \(\Delta NMC\)có: \(\widehat {AMD} = \widehat {NMC}\) (đối đỉnh), \(MD = MC\left( {gt} \right)\); \(\widehat {{D_1}} = \widehat {{C_1}}\) (vì AD // BC), nên

\(\Delta AMD = \Delta NMC\)(c.g.c).

Suy ra AM = NM.

Xét \(\Delta HAM\) và \(\Delta KNM\)có: \(\widehat H = \widehat K = {90^0}\) , \(\widehat {{M_1}} = \widehat {{M_2}},AM = NM\) , nên \(\Delta HAM = \Delta KNM\left( {c.h.g.n} \right)\)

Suy ra \(AH = NK\).

AH chính là khoảng cách của d và d’, d’ cố định nên N thuộc đường thẳng cố định m song song với d’ cách d’ một khoảng bằng khoảng cách của d và d’. 

Phương pháp giải:

+ Vẽ thêm N là trung điểm của AH.

+ Ta chứng minh MH//IN, KH//IN, từ đó suy ra M, H, K thẳng hàng.

Lời giải chi tiết:

Tam giác EAM vuông tại E, EI là đường trung tuyến nên:  \(EI = IM = IA = {1 \over 2}AM\)

Từ EI = IA suy ra tam giác IAE cân tại I, từ đó có: \(\widehat {EIM} = 2\widehat {EAI}\) (góc ngoài của tam giác).

Chứng minh tương tự với tam giác vuông  ta có:  \(\widehat {MID} = 2\widehat {IAD},DI = {1 \over 2}AM\)

Do đó:

\(EI = DI\,\,\left( { = {1 \over 2}AM} \right);\,\,\,\widehat {EID} = \widehat {EIM} + \widehat {MID} = 2\left( {\widehat {EAI} + \widehat {IAD}} \right) = 2\widehat {EAD} = {60^0}\)

Tam giác IED cân (vì EI = DI) có \(\widehat {EID} = {60^0}\) nên là tam giác đều, từ đó EI = ED = ID.

Tương tự  tam giác IDF đều suy ra ID = DF = IF.

Do đó EI = ED = DF = IF. Suy ra tứ giác EIFD là hình thoi.

Suy ra K là trung điểm chung của EF và ID.

Gọi N là trung điểm của AH.

Tam giác ABC đều có H là trực tâm của tam giác ABC nên H cũng là trọng tâm tam giác.

Do đó AN = NH = HD.

Ta có : MH // IN ( vì IN là đường trung bình của tam giác AMH) và KH // IN(vì KH là đường trung bình của tam giác DIN).

Từ H ta chỉ vẽ được một đường thẳng song song với IN (tiên đề Ơ – Clit) nên M, H, K thẳng hàng.