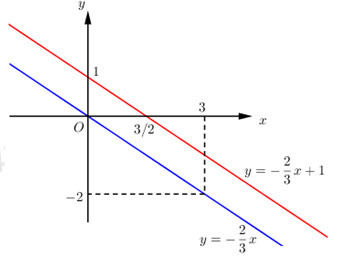
20 bài tập tổng hợp về Đường thẳng song song và đường thẳng cắt nhauLàm bàiCâu hỏi 1 : Vẽ đồ thị \(y = \dfrac{{ - 2}}{3}x\) và \(y = \dfrac{{ - 2}}{3}x + 1\) trên cùng một hệ trục tọa độ \(Oxy\) và nhận xét về đồ thị của hai hàm số này. Phương pháp giải: Cách vẽ đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\). Cho \(x = 0 \Rightarrow y = b \Rightarrow A\left( {0;b} \right)\) Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a} \Rightarrow B\left( { - \dfrac{b}{a};0} \right)\) Vẽ đường thẳng đi qua hai điểm \(A\left( {0;b} \right)\) và \(B\left( { - \dfrac{b}{a};0} \right)\). Lời giải chi tiết: \(y = \dfrac{{ - 2}}{3}x\) đi qua \(A\left( {0;0} \right)\)và \(B\left( {3; - 2} \right)\) \(y = \dfrac{{ - 2}}{3}x + 1\) đi qua \(A\left( {0;1} \right)\)và \(B\left( {\dfrac{3}{2};0} \right)\) Từ đó ta có đồ thị.
Nhìn trên đồ thị ta có 2 đồ thị song song với nhau . Câu hỏi 2 : Chọn đáp án đúng nhất: Câu 1: Không sử dụng máy tính cầm tay, giải hệ phương trình: \(\left\{ \begin{array}{l}4x - y = 7\\x + 3y = 5\end{array} \right..\)
Đáp án: D Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số. Lời giải chi tiết: \(\left\{ \begin{array}{l}4x - y = 7\\x + 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12x - 3y = 21\\x + 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}13x = 26\\y = 4x - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 4.2 - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\) Vậy hệ phương trình có nghiệm duy nhất:\(\left( {x;\,\,y} \right) = \left( {2;\,1} \right).\) Chọn D. Câu 2: Cho đường thẳng \(d:\,\,y = ax + b.\) Tìm giá trị của \(a,\,\,b\) sao cho đường thẳng \(d\) đi qua điểm \(A\left( {0; - 1} \right)\) và song song với đường thẳng \(\Delta :\,\,y = x + 2019.\)
Đáp án: B Phương pháp giải: Hai đường thẳng \({d_1}:\,\,y = {a_1}x + {b_1},\,\,{d_2}:\,\,y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Lời giải chi tiết: Ta có: \(d//\Delta \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b \ne 2019\end{array} \right. \Rightarrow d:\,\,y = x + b,\left( {b \ne 2019} \right).\) Đường thẳng \(d:\,\,y = x + b\) đi qua điểm \(A\left( {0; - 1} \right)\) nên thay tọa độ điểm \(A\) vào phương trình đường thẳng \(d\) ta được: \( - 1 = 0 + b \Leftrightarrow b = - 1\,\,\left( {tm} \right)\) Vậy \(a = 1;\,\,b = - 1.\) Chọn B. Câu hỏi 3 : Tìm \(m\) để đường thẳng \(\left( d \right):\,\,y = {m^2}x + m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 4x - 2.\)
Đáp án: D Phương pháp giải: Cho hai đường thẳng \(d:\,\,y = ax + b\) và \(d':\,\,y = a'x + b'.\) Khi đó: \(d//d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\) Lời giải chi tiết: \(\left( d \right):\,\,y = {m^2}x + m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 4x - 2.\) \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\m \ne - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne - 2\end{array} \right. \Leftrightarrow m = 2.\) Chọn D. Câu hỏi 4 : Đường thẳng nào sau đây không song song với đường thẳng \(y = 7x + 3?\)
Đáp án: B Phương pháp giải: Hai đường thẳng \(\left( d \right):y = ax + b,\left( {d'} \right):y = a'x + b'\) +) song song với nhau khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) +) Cắt nhau khi \(a \ne a'\) Lời giải chi tiết: Đường thẳng \(y = 7x + 3\) và đường thẳng \(y = 4 - 7x\) có \(7 \ne - 7\) nên hai đường thẳng này cắt nhau tức là chúng không song song. Chọn B Câu hỏi 5 : Đường thẳng nào sau đây song song với đường thẳng \(y = - 2x + 3?\)
Đáp án: A Phương pháp giải: Hai đường thẳng \({d_1}:\,\,\,y = {a_1}x + {b_1}\) và \({d_2}:\,\,\,y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Lời giải chi tiết: Đường thẳng song song với đường thẳng \(y = - 2x + 3\) có dạng: \(y = - 2x + b\,\,\,\,\left( {b \ne 3} \right).\) \( \Rightarrow \) Chỉ có đáp án A: \(y = - 2x + 7\) thỏa mãn. Chọn A. Câu hỏi 6 : Giá trị của \(m\) để đồ thị các hàm số \(y = \left( {m + 2} \right)x + 3\) và \(y = 3x + 3\) trùng nhau là
Đáp án: A Phương pháp giải: Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) trùng nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} = {b_2}\end{array} \right.\). Lời giải chi tiết: Đồ thị các hàm số \(y = \left( {m + 2} \right)x + 3\) và \(y = 3x + 3\)\( \Leftrightarrow \left\{ \begin{array}{l}m + 2 = 3\\3 = 3\end{array} \right. \Leftrightarrow m = 1\). Chọn A. Câu hỏi 7 : Giá trị của tham số \(m\) để đường thẳng \(y = mx + 1\) song song với đường thẳng \(y = 2x - 3\) là:
Đáp án: C Phương pháp giải: Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Lời giải chi tiết: Đường thẳng \(y = mx + 1\) song song với đường thẳng \(y = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}m = 2\\1 \ne - 3\end{array} \right. \Leftrightarrow m = 2.\) Chọn C. Câu hỏi 8 : Tìm \(m\) để hai đường thẳng \({d_1}:\,\,\,y = 2mx + 3\) và \({d_2}:\,\,\,y = \left( {m + 1} \right)x + 2\) song song.
Đáp án: B Phương pháp giải: Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Lời giải chi tiết: Ta có: \({d_1}:\,\,\,y = 2mx + 3\) và \({d_2}:\,\,y = \left( {m + 1} \right)x + 2\) song song \( \Leftrightarrow \left\{ \begin{array}{l}2m = m + 1\\3 \ne 2\end{array} \right. \Leftrightarrow m = 1.\) Chọn B. Câu hỏi 9 : Cho 2 đường thẳng \(\left( {{d_1}} \right):y = \left( {{m^2} + 1} \right)x + 2\) và \(\left( {{d_2}} \right):y = 5x + m\). Hai đường thẳng đó trùng nhau khi:
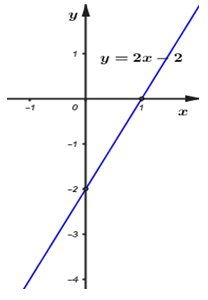
Đáp án: B Phương pháp giải: Hai đường thẳng trùng nhau khi chúng có các hệ số giống hệt nhau Lời giải chi tiết: Hai đường thẳng đề cho trùng nhau khi: \(\left\{ \begin{array}{l}{m^2} + 1 = 5\\m = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \pm 2\\m = 2\end{array} \right. \Leftrightarrow m = 2\) Chọn đáp án B Câu hỏi 10 : Cho hàm số \(y = 2x - 2\). a) Hàm số đã cho đồng biến hay nghịch biến trên \(\mathbb{R}\). Vì sao? b) Vẽ đồ thị hàm số \(y = 2x - 2\). c) Với giá trị nào của \(m\) thì đường thẳng \(y = (m - 1)x + 3\,\,\,\,\,(m \ne 1)\)song song với đường thẳng \(y = 2x - 2\).
Đáp án: B Phương pháp giải: a) Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R}\) khi \(a > 0\). b) Tìm các 2 điểm bất kì thuộc đồ thị hàm số. Đồ thị hàm số là đường thẳng đi qua 2 điểm đó. c) Đường thẳng \(y = (m - 1)x + 3\,\,(m \ne 1)\) song song với đường thẳng \(y = 2x - 2\) khi hệ số góc của hai hàm số bằng nhau và hệ số tự do của 2 đường thẳng khác nhau. Lời giải chi tiết: a) Hàm số đã cho đồng biến trên \(\mathbb{R}\) vì \(a = 2 > 0\). b) Vẽ đồ thị hàm số \(y = 2x - 2\) Cho \(x = 0 \Rightarrow y = - 2\), ta được điểm \((0; - 2)\) thuộc đường thẳng \(y = 2x - 2\); \(y = 0 \Rightarrow x = 1\), ta được điểm \((1;0)\) thuộc đường thẳng \(y = 2x - 2\). Vậy đồ thị hàm số \(y = 2x - 2\) là đường thẳng đi qua 2 điểm \(\left( {0; - 2} \right),\;\left( {1;\;0} \right).\;\) Đồ thị hàm số như hình vẽ bên: c) Đường thẳng \(y = (m - 1)x + 3\,\,(m \ne 1)\) song song với đường thẳng \(y = 2x - 2\) \(\begin{array}{l} \Leftrightarrow m - 1 = 2\\ \Leftrightarrow m = 3\end{array}\) (vì \(3 \ne - 2\)) Chọn B. Câu hỏi 11 : Cho hàm số \(y = \left( {{m^2} - 2m + 3} \right)x - 4\,\,\,\,\,\left( d \right)\), (với m là tham số) 1. Chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó. 2. Tìm m để \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\). 3. Tìm m để \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\).
Đáp án: D Phương pháp giải: 1. Hàm số \(y = ax + b\) đồng biến khi \(a > 0\) 2. \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\) thì tọa độ điểm A thỏa mãn hàm số của \(\left( d \right)\) 3. \(y = ax + b\) song song với \(y = a'x + b'\) \( \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) Lời giải chi tiết: Cho hàm số \(y = \left( {{m^2} - 2m + 3} \right)x - 4\,\,\,\,\,\left( d \right)\), (với m là tham số) 1. Chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó. \({m^2} - 2m + 3 = {m^2} - 2m + 1 + 2 = {\left( {m - 1} \right)^2} + 2 > 0\) với mọi m Vậy với mọi m hàm số luôn đồng biến trên tập xác định của nó 2. Tìm m để \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\). Để \(\left( d \right)\) đi qua \(A\left( {2;8} \right) \Leftrightarrow 8 = \left( {{m^2} - 2m + 3} \right).2 - 4 \Leftrightarrow 2{m^2} - 4m + 6 - 4 - 8 = 0\) \(\begin{array}{l} \Leftrightarrow 2{m^2} - 4m - 6 = 0 \Leftrightarrow 2{m^2} + 2m - 6m - 6 = 0\\ \Leftrightarrow 2m\left( {m + 1} \right) - 6\left( {m + 1} \right) = 0 \Leftrightarrow \left( {m + 1} \right)\left( {2m - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\2m - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 3\end{array} \right.\end{array}\) Vậy với \(m = - 1\) hoặc \(m = 3\) thì \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\) 3. Tìm m để \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\). Để \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\) \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m + 3 = 3\\ - 4 \ne m - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m = 0\\m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m\left( {m - 2} \right) = 0\\m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\\m \ne 0\end{array} \right. \Leftrightarrow m = 2.\) Vậy với \(m = 2\) thì \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\). Chọn D. Câu hỏi 12 : Tìm tọa độ giao điểm của đường thẳng \({d_1}:\,y = 2x + 1\) và đường thẳng \({d_2}:y = x + 3.\)
Đáp án: A Phương pháp giải: Cách 1: Giải phương trình hoành độ giao điểm. Cách 2 : Giải hệ phương trình bao gồm 2 phương trình đường thẳng. Lời giải chi tiết: Cách 1: Phương trình hoành độ giao điểm của \({d_1},\,{d_2}\) là: \(2x + 1 = x + 3 \Leftrightarrow 2x - x = 3 - 1 \Leftrightarrow x = 2\) Thay \(x = 2\) vào d2 ta có: \(y = x + 3 = 2 + 3 = 5\). Vậy \(A\left( {2;5} \right)\) là giao điểm của hai đường thẳng. Cách 2: Gọi \(A\left( {x;y} \right)\) là giao điểm của \({d_1}\) và \({d_2}\). Tọa độ của \(A\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}y = 2x + 1\\y = x + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = - 1\\x - y = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\x - y = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5\end{array} \right.\). Vậy \(A\left( {2;5} \right)\). Chọn A. Câu hỏi 13 : Cho hàm số \(y = ax + b\) với \(a \ne 0\) . Xác định các hệ số \(a,b\) biết đồ thị hàm số song song với đường thẳng \(y = 2x + 2019\) và cắt trục tung tại điểm có tung độ là 2020.
Đáp án: D Phương pháp giải: Đồ thị hàm số song song với đường thẳng \(y = 2x + 2019\)suy ra \(\left\{ \begin{array}{l}a = 0\\b \ne 2019\end{array} \right..\) Đồ thị hàm số cắt trục tung tại điểm có tung độ là 2020, suy ra tọa độ giao điểm \(A\left( {0;2020} \right)\) Lời giải chi tiết: Vì đồ thị hàm số \(y = ax + b\) song song với đường thẳng \(y = 2x + 2019\) nên \(\left\{ \begin{array}{l}a = 0\\b \ne 2019\end{array} \right..\) \( \Rightarrow y = ax + b \Leftrightarrow y = 2x + b\,\,\,\left( {b \ne 2019} \right)\) Mà đồ thị hàm số cắt trục tung tại điểm có tung độ là \(2020 \Rightarrow \) đồ thị hàm số đi qua điểm \(\left( {0;\,\,\,2020} \right)\) \(\begin{array}{l} \Rightarrow 2020 = 2.0 + b\\ \Rightarrow b = 2020\,\,\,\left( {tm} \right)\end{array}\) Vậy \(a = 2;\,\,\,\,b = 2020.\) Chọn D. Câu hỏi 14 : Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = - \frac{2}{3}x + 5\) và đi qua điểm \(A\left( {0;2} \right).\) Khi đó tổng \(S = a + b\) là
Đáp án: D Phương pháp giải: +) Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\). +) Thay tọa độ điểm \(A\) vào phương trình đường thẳng. Lời giải chi tiết: Gọi đường thẳng cần tìm là \(d\). Do \(d\) song song với đường thẳng \(y = - \frac{2}{3}x + 5 \Rightarrow \) Phương trình đường thẳng d có dạng \(y = - \frac{2}{3}x + c\,\,\left( {c \ne 5} \right)\). Do \(A\left( {0;2} \right) \in d \Rightarrow 2 = - \frac{2}{3}.0 + c \Leftrightarrow c = 2\). Vậy phương trình đường thẳng d là \(y = - \frac{2}{3}x + 2 \Rightarrow \left\{ \begin{array}{l}a = - \frac{2}{3}\\b = 2\end{array} \right. \Rightarrow S = a + b = - \frac{2}{3} + 2 = \frac{4}{3}\). Chọn D. Câu hỏi 15 : Giá trị của tham số \(m\) để ba đường thẳng \(\left( {{d_1}} \right):y = 2x - 5,\,\left( {{d_2}} \right):y = 1\) và \(\left( {{d_3}} \right):y = \left( {2m - 3} \right)x - 2\) đồng quy tại một điểm là
Đáp án: D Phương pháp giải: +) Tìm tọa độ giao điểm \(M\) của đường thẳng \({\left( d \right)_1},\,\,\left( {{d_2}} \right).\) +) Ba đường thẳng \(\left( {{d_1}} \right);\,\,\left( {{d_2}} \right);\,\,\left( {{d_3}} \right)\) đồng quy \( \Leftrightarrow M \in \left( {{d_3}} \right).\) +) Thay tọa độ điểm \(M\) vào công thức đường thẳng\(\left( {{d_3}} \right)\) để tìm \(m.\) Lời giải chi tiết: Ta có tọa độ giao điểm \(M\) của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là nghiệm của hệ phương trình : \(\left\{ \begin{array}{l}y = 2x - 5\\y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right. \Rightarrow M\left( {3;\,\,1} \right).\) Ba đường thẳng \(\left( {{d_1}} \right);\,\,\left( {{d_2}} \right);\,\,\left( {{d_3}} \right)\) đồng quy \( \Leftrightarrow M \in \left( {{d_3}} \right).\) \( \Leftrightarrow 1 = \left( {2m - 3} \right).3 - 2 \Leftrightarrow 1 = 6m - 9 - 2 \Leftrightarrow m = 2.\) Chọn D. Câu hỏi 16 : Chọn đáp án đúng nhất: Câu 1: Tìm các giá trị của tham số \(m\) để đồ thị hai hàm số \(y = \left( {m + 4} \right)x + 11\) và \(y = x + {m^2} + 2\) cắt nhau tại một điểm trên trục tung.
Đáp án: C Phương pháp giải: Xét phương trình hoành độ giao điểm. Để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung thì tìm điều kiện để phương trình hoành độ giao điểm có nghiệm duy nhất \(x = 0\) Lời giải chi tiết: Xét phương trình hoành độ giao điểm của hai hàm số ta có: \(\left( {m + 4} \right)x + 11 = x + {m^2} + 2 \Leftrightarrow \left( {m + 3} \right)x = {m^2} - 9\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\) Để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung thì phương trình (1) có nghiệm duy nhất \(x = 0\) \( \Leftrightarrow \left\{ \begin{array}{l}m + 3 \ne 0\\x = \frac{{{m^2} - 9}}{{m + 3}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m = 3\end{array} \right. \Rightarrow m = 3\) Vậy \(m = 3.\) Chọn C. Câu 2: Giải hệ phương trình \(\left\{ \begin{array}{l}3x - \frac{2}{{y + 1}} = - \frac{1}{2}\\2x + \frac{1}{{y + 1}} = 2\end{array} \right..\)
Đáp án: A Phương pháp giải: Đặt \(t = \frac{1}{{y + 1}}\) và giải hệ phương trình bằng phương pháp cộng đại số ra \(x,\,t\). Từ đó tìm được \(x,\,y\). Lời giải chi tiết: Điều kiện: \(y \ne - 1\) Đặt \(t = \frac{1}{{y + 1}}\) Hệ phương trình \( \Leftrightarrow \left\{ \begin{array}{l}3x - 2t = - \frac{1}{2}\\2x + t = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 2t = - \frac{1}{2}\\4x + 2t = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = \frac{7}{2}\\2x + t = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\t = 1\end{array} \right..\) Với \(t = 1\) thì \(\frac{1}{{y + 1}} = 1 \Rightarrow y + 1 = 1 \Leftrightarrow y = 0\,\,\,\,\left( {tm} \right)\) Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\frac{1}{2};0} \right)\) Chọn A. Câu hỏi 17 : Cho đường thẳng \(\left( {{d_1}} \right):\,\,y = ax + b\) song song với đường thẳng \(\left( {{d_2}} \right):\,\,\,y = 2x + 2019\) và cắt trục tung tại điểm \(A\left( {0; - 2} \right).\) Giá trị của biểu thức \({a^2} + {b^3}\) bằng:
Đáp án: C Phương pháp giải: Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\) Lời giải chi tiết: Theo đề bài ta có:\({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 2019\end{array} \right. \Rightarrow {d_1}:\,\,\,y = 2x + b.\) \({d_1}\) cắt trục tung tại \(A\left( {0; - 2} \right) \Rightarrow - 2 = 2.0 + b \Leftrightarrow b = - 2\,\,\left( {tm} \right)\) \( \Rightarrow {a^2} + {b^3} = {2^2} + {\left( { - 2} \right)^3} = 4 - 8 = - 4.\) Chọn C. Câu hỏi 18 : Trong hệ trục tọa độ \(Oxy\) cho hai đường thẳng \(\left( {{d_1}} \right):\,\,y = 5x + 9\) và \(\left( {{d_2}} \right):\,\,y = \left( {{m^2} - 4} \right)x + 3m\) (\(m\) là tham số). Tìm các giá trị của \(m\) để hai đường thẳng \({d_1}\) và \({d_2}\) song song.
Đáp án: C Phương pháp giải: Cho hai đường thẳng: \({d_1}:\,\,\,y = {a_1}x + {b_1}\) và \({d_2}:\,\,\,y = {a_2}x + {b_2}.\) Khi đó: \({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Lời giải chi tiết: Ta có hai đường thẳng \(\left( {{d_1}} \right):\,\,y = 5x + 9\) và \(\left( {{d_2}} \right):\,\,y = \left( {{m^2} - 4} \right)x + 3m\) song song \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4 = 5\\3m \ne 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 9\\m \ne 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 3\\m = - 3\end{array} \right.\\m \ne 3\end{array} \right. \Leftrightarrow m = - 3.\) Vậy \(m = - 3\) thì đường thẳng \({d_1}\) và \({d_2}\) song song. Chọn C. Câu hỏi 19 : Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\) \(\left( {m \ne 4} \right)\). a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\) b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút). c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\)
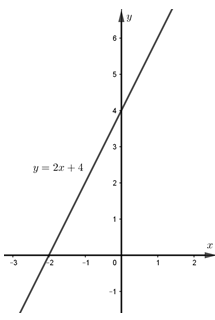
Đáp án: A Phương pháp giải: a) Thay tọa độ điểm A vào hàm số để tìm m b) Sử dụng định nghĩa hệ số góc của đường thẳng để tính góc cần tìm c) Áp dụng điều kiện để hai đường thẳng song song để tìm m Lời giải chi tiết: Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\) \(\left( {m \ne 4} \right)\). a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\) \(A\left( {1;\;6} \right)\) thuộc đường thẳng \(\left( d \right).\) Ta thay \(x = 1;\,\,y = 6\) vào hàm số \(y = \left( {m - 4} \right)x + 4\) ta được \(6 = \left( {m - 4} \right).1 + 4 \Leftrightarrow m = 6\;\;\left( {tm} \right)\) Vậy với \(m = 6\) thì đồ thị hàm số đi qua \(A\left( {1;6} \right)\) b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút). Với \(m = 6\) thì \(y = 2x + 4\) Ta có bảng giá trị: Đường thẳng \(y = 2x + 4\) đi qua hai điểm \(\left( {0;4} \right)\) và \(\left( { - 2;0} \right)\) Gọi \(\alpha \) là góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox \( \Rightarrow \tan \alpha = 2 \Rightarrow \alpha \approx {63^0}26'\) c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\) \(\left( d \right)//\left( {{d_1}} \right) \Leftrightarrow \left\{ \begin{array}{l}m - {m^2} = m - 4\\m + 2 \ne 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} = 4\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = - 2\;\;\left( {tm} \right)\) Vậy với \(m = - 2\) thỏa mãn yêu cầu đề bài. Câu hỏi 20 : Cho hàm số \(y = 0,5x\) có đồ thị là \(\left( {{d_1}} \right)\) và hàm số \(y = - x + 3\) có đồ thị là \(\left( {{d_2}} \right)\). a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ Oxy. b) Xác định các hệ số a, b của đường thẳng \(\left( {{d_3}} \right)\)\(:\,\,y = ax + b\). Biết \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 4.
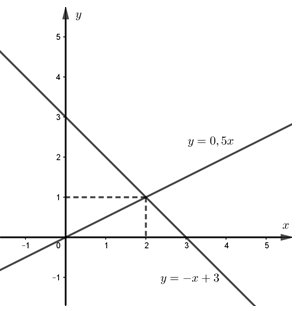
Đáp án: B Phương pháp giải: a) Lập bảng giá trị và vẽ đồ thị hàm số. b) Tìm điểm\(A\left( {4;{y_0}} \right)\) là giao điểm của \(\left( {{d_3}} \right)\) và \(\left( {{d_2}} \right)\), \(\left( {{d_3}} \right)//\left( {{d_1}} \right)\) suy ra a và dạng của \(\left( {{d_3}} \right)\), thay tọa độ điểm A vào đó để suy ra b Lời giải chi tiết: Cho hàm số \(y = 0,5x\) có đồ thị là \(\left( {{d_1}} \right)\) và hàm số \(y = - x + 3\) có đồ thị là \(\left( {{d_2}} \right)\). a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ Oxy.
\( \Rightarrow \left( {{d_1}} \right)\) là đường thẳng đi qua gốc tọa độ và điểm \(\left( {2;1} \right)\) \( \Rightarrow \left( {{d_2}} \right)\) là đường thẳng đi qua 2 điểm \(\left( {0;3} \right)\) và \(\left( {3;0} \right)\) b) Xác định các hệ số a, b của đường thẳng \(\left( {{d_3}} \right)\)\(:\,\,y = ax + b\). Biết \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 4. \(\left( {{d_3}} \right)//\left( {{d_1}} \right) \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b \ne 0\end{array} \right.\,\,\,\, \Rightarrow \,\,\left( {{d_3}} \right):\,\,y = \frac{1}{2}x + b\) Gọi \(A\left( {4;{y_0}} \right)\) là giao điểm của \(\left( {{d_3}} \right)\) và \(\left( {{d_2}} \right)\) \(A\left( {4;{y_0}} \right) \in \left( {{d_2}} \right) \Leftrightarrow {y_0} = - 4 + 3 = - 1 \Rightarrow A\left( {4; - 1} \right)\) \(A\left( {4; - 1} \right) \in \left( {{d_3}} \right) \Leftrightarrow - 1 = \frac{1}{2}.4 + b \Leftrightarrow - 1 = 2 + b \Leftrightarrow b = - 3\) (tmđk \(b \ne 0\)) Vậy \(\left( {{d_3}} \right):y = \frac{1}{2}x - 3\) Chọn B. |