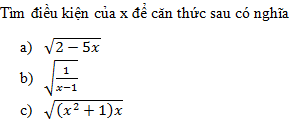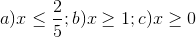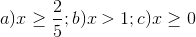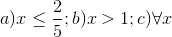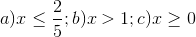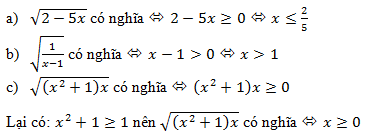Phương pháp giải:

Biểu thức $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

Biểu thức $\sqrt {x - 3}$  xác định $\Leftrightarrow x - 3 \ge 0 \Leftrightarrow x \ge 3.$

Chọn D.

Phương pháp giải:

Biểu thức $\sqrt A$ xác định khi $A \ge 0$

Lời giải chi tiết:

Ta có: $\sqrt {x - 8}$ xác định khi $x - 8 \ge 0 \Leftrightarrow x \ge 8$

Chọn A

Phương pháp giải:

Hàm số $y = \sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

Biểu thức $\sqrt {2x - 8}$ xác định $\Leftrightarrow 2x - 8 \ge 0 \Leftrightarrow 2x \ge 8 \Leftrightarrow x \ge 4.$

Chọn D.

Phương pháp giải:

Biểu thức $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$ 

Lời giải chi tiết:

Xét đáp án A: $\sqrt {2 - x}$ xác định $\Leftrightarrow 2 - x \ge 0 \Leftrightarrow x \le 2 \Rightarrow$ loại đáp án A.

Xét đáp án B: $\sqrt {x - 2}$ xác định $\Leftrightarrow x - 2 \ge 0 \Leftrightarrow x \ge 2 \Rightarrow$ loại đáp án B.

Xét đáp án C:$\sqrt {2x}$ xác định $\Leftrightarrow 2x \ge 0 \Leftrightarrow x \ge 0 \Rightarrow$ chọn đáp án C.

Chọn C.

Phương pháp giải:

$\sqrt A$ xác định $\Leftrightarrow A \ge 0$.

Lời giải chi tiết:

Biểu thức $\sqrt { - {x^2} + 6x - 9}$ xác định $\Leftrightarrow  - {x^2} + 6x - 9 \ge 0$.

$\Leftrightarrow {x^2} - 6x + 9 \le 0 \Leftrightarrow {\left( {x - 3} \right)^2} \le 0\,\,\left( * \right)$.

Do ${\left( {x - 3} \right)^2} \ge 0\,\,\forall x \Rightarrow \left( * \right) \Leftrightarrow x - 3 = 0 \Leftrightarrow x = 3$.

Chọn C.

Phương pháp giải:

- $\sqrt A$ xác định (hay có nghĩa) khi $A \ge 0$.

- Phân thức $\frac{{A(x)}}{{B(x)}}$ xác định khi $B(x) \ne 0$.

Lời giải chi tiết:

+) $\frac{{2017}}{{x - 2018}}$ xác định khi $x - 2018 \ne 0\,\, \Leftrightarrow x \ne 2018\,\,\,\,\,\,\,\,\,\,\,\,(1)$    

+) $\sqrt {\frac{{2017}}{{x - 2018}}}$  xác định $\Leftrightarrow \frac{{2017}}{{x - 2018}} \ge 0 \Leftrightarrow x - 2108 > 0 \Leftrightarrow x > 2018.\;\;\;\;\left( 2 \right)$

Kết hợp (1) và (2) suy ra $x > 2018$.

Vậy điều kiện xác định của biểu thức$\sqrt {\frac{{2017}}{{x - 2018}}}$  là $x > 2018$.

Chọn C.

Phương pháp giải:

Biểu thức$\sqrt A$ xác định $\Leftrightarrow A \ge 0$

Lời giải chi tiết:

$\sqrt {1 - {y^2}}$xác định $\Leftrightarrow 1 - {y^2} \ge 0 \Leftrightarrow {y^2} \le 1 \Leftrightarrow \, - 1 \le y \le 1$

Chọn C

Phương pháp giải:

Điều kiện để $\sqrt A$ có nghĩa là $A \ge 0.$

Lời giải chi tiết:

$\sqrt {3 - x}$ có nghĩa $\Leftrightarrow 3 - x \ge 0 \Leftrightarrow x \le 3.$

Chọn A

Phương pháp giải:

Biểu thức $\sqrt {f\left( x \right)}$ có nghĩa $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

Biểu thức $\sqrt {3x - 6}$ xác định $\Leftrightarrow 3x - 6 \ge 0 \Leftrightarrow x \ge 2.$ 

Chọn  B.

Phương pháp giải:

Biểu thức: $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$ 

Lời giải chi tiết:

Biểu thức $P = \sqrt {x - 2}$ xác định $\Leftrightarrow x - 2 \ge 0 \Leftrightarrow x \ge 2.$

Chọn C.

Phương pháp giải:

Biểu thức $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

Biểu thức $\sqrt {2019 - \frac{{2019}}{x}}$ xác định

$\Leftrightarrow 2019 - \frac{{2019}}{x} \ge 0 \Leftrightarrow \frac{{2019\left( {x - 1} \right)}}{x} \ge 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 \ge 0\\x > 0\end{array} \right.\\\left\{ \begin{array}{l}x - 1 \le 0\\x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x < 0\end{array} \right..$

Chọn C.

Phương pháp giải:

Biểu thức $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

Biểu thức $\sqrt {2019 - 3x}  + x - 2020$ xác định $\Leftrightarrow 2019 - 3x \ge 0 \Leftrightarrow x \le 673.$

Chọn B.

Phương pháp giải:

Biểu thức $\frac{1}{{f\left( x \right)}}$ xác định $\Leftrightarrow f\left( x \right) \ne 0.$

Biểu thức $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

Ta có: $M = \frac{1}{{\sqrt x  - 1}}$ xác định $\Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\sqrt x  - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 1\end{array} \right..$

Chọn D.

Phương pháp giải:

Biểu thức $\sqrt A$ xác định $\Leftrightarrow A \ge 0.$

Lời giải chi tiết:

Ta có: $\sqrt {{x^2} + 5x - 6}  = \sqrt {\left( {x - 1} \right)\left( {x + 6} \right)}$

Để $\sqrt {{x^2} + 5x - 6}$có nghĩa thì $\left( {x - 1} \right)\left( {x + 6} \right) \ge 0$

 $\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 \ge 0\\x + 6 \ge 0\end{array} \right.\\\left\{ \begin{array}{l}x - 1 \le 0\\x + 6 \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x \ge  - 6\end{array} \right.\\\left\{ \begin{array}{l}x \le 1\\x \le  - 6\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le  - 6\end{array} \right.$

Chọn D.

Phương pháp giải:

Biểu thức $\dfrac{1}{{\sqrt {f\left( x \right)} }}$ xác định $\Leftrightarrow f\left( x \right) > 0.$

Lời giải chi tiết:

Biểu thức $P = \dfrac{1}{{\sqrt {{x^2} - 6x + 9} }}$ xác định $\Leftrightarrow {x^2} - 6x + 9 > 0$ $\Leftrightarrow {\left( {x - 3} \right)^2} > 0 \Leftrightarrow x - 3 \ne 0 \Leftrightarrow x \ne 3.$

Vậy với $x \ne 3$ thì biểu thức $P = \dfrac{1}{{\sqrt {{x^2} - 6x + 9} }}$ xác định.

Chọn D.

Phương pháp giải:

Hàm số $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0.$

Lời giải chi tiết:

$\sqrt {6 - 3x}$  xác định $\Leftrightarrow 6 - 3x \ge 0 \Leftrightarrow 3x \le 6 \Leftrightarrow x \le 2.$

Chọn A.

Phương pháp giải:

Phân thức xác định khi và chỉ khi mẫu thức khác 0.

Lời giải chi tiết:

Biểu thức $P = \sqrt[3]{{\frac{{x - 3}}{{{x^2} - 3x + 2}}}}$ xác định $\Leftrightarrow {x^2} - 3x + 2 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne 2\end{array} \right.$.

Chọn A.

Phương pháp giải:

Cách tìm điều kiện xác định của 1 phân thức : biểu thức dưới mẫu khác 0, biểu thức trong căn lớn hơn hoặc bằng 0

Lời giải chi tiết:

Biểu thức $A = \frac{{2017}}{{\sqrt x  - 1}}$ xác định $\Leftrightarrow \left\{ \begin{array}{l}\sqrt x  - 1 \ne 0\\x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt x  \ne 1\\x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ge 0\end{array} \right.$

Chọn đáp án D

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

a) $\sqrt {2 - 5x}$ có nghĩa $\Leftrightarrow 2 - 5x \ge 0 \Leftrightarrow  - 5x \ge  - 2 \Leftrightarrow x \le \frac{2}{5}.$

b) $\frac{1}{{\sqrt {1 - x} }}$ xác định $\Leftrightarrow \left\{ \begin{array}{l}\sqrt {1 - x}  \ne 0\\1 - x \ge 0\end{array} \right. \Leftrightarrow 1 - x > 0 \Leftrightarrow x < 1.$

c) $\sqrt {{x^2} - 4x + 4}$ xác định $\Leftrightarrow {x^2} - 4x + 4 \ge 0 \Leftrightarrow {\left( {x - 2} \right)^2} \ge 0$  luôn đúng với mọi $x.$

d) $\frac{1}{{\sqrt {{x^2} - 4x + 4} }}$ có nghĩa $\Leftrightarrow {x^2} - 4x + 4 > 0 \Leftrightarrow {\left( {x - 2} \right)^2} > 0 \Leftrightarrow x - 2 \ne 0 \Leftrightarrow x \ne 2.$