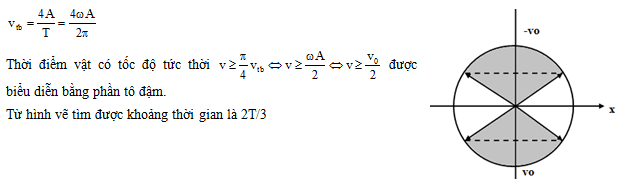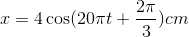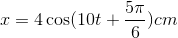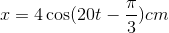40 bài tập dao động điều hòa mức độ thông hiểuLàm bàiCâu hỏi 1 : Một vật dao động điều hòa với chu kỳ 2s, biên độ A = 5 cm. Xác định quãng đường lớn nhất vật đi được trong
Đáp án: A Phương pháp giải: Lời giải chi tiết: ∆t = => Câu hỏi 2 : Vật dao động điều hòa trên phương trình x = 4cos(4πt + π/6) cm. Thời điểm vật đi qua vị trí có li độ x = 2cm theo chiều dương là:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Vật qua li độ x = 2cm theo chiều dương được biểu diễn tương ứng với điểm M trên VTLG: Từ VTLG ta có vật qua vị trí x = 2cm có pha dao động là \( - {\pi \over 3}\) \( \Rightarrow 4\pi t + {\pi \over 6} = - {\pi \over 3} + k2\pi \Leftrightarrow 4t = - {1 \over 2} + 2k \Rightarrow t = - {1 \over 8} + {k \over 2}\,\,\left( s \right);\,k = 1;2;3;...\) Chọn A Câu hỏi 3 : Một vật khối lượng 1 kg dao động điều hòa với phương trình: x = 10cos(
Đáp án: A Phương pháp giải: Phương pháp: Áp dụng công thức tính lực kéo về vật dao động điều hoà: Lực kéo về F = - kx Lời giải chi tiết: Đáp án A Khi t = 0,5s thì x = -10cm Lực kéo về tác dụng lên vật: F = -kx = \( - m{\omega ^2}x\) = 1N
Câu hỏi 4 : Phương trình li độ của 3 dao động điều hòa có dạng sau:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Phương pháp: φ = 2kπ (cùng pha); φ = (2k + 1)π (ngược pha); φ = (2k + 1)π/2 (vuông pha) \(\eqalign{ & {{\rm{x}}_1} = 3c{\rm{os}}\left( {\pi t - {\pi \over 2}} \right)cm \cr & {{\rm{x}}_2} = 4\sin \left( {\pi t - {\pi \over 2}} \right)cm = 4c{\rm{os}}\left( {\pi t - \pi } \right)cm \cr & {{\rm{x}}_3} = 5\sin \left( {\pi t} \right)cm = 5c{\rm{os(}}\pi {\rm{t - }}{\pi \over 2})cm \cr} \) Vậy x1, x2 vuông pha. Câu hỏi 5 : Hai dao động có phương trình lần lượt là: x1 = 5cos(2πt + 0,75π) (cm) và x2 = 10cos(2πt + 0,5π) (cm). Độ lệch pha của hai dao động này có độ lớn bằng
Đáp án: A Phương pháp giải: Sử dụng công thức: $$\Delta \varphi = \left| {{\varphi _1} - {\varphi _2}} \right|$$ Lời giải chi tiết: Đáp án A: Ta có độ lệch pha giữa hai dao động: $$\Delta \varphi = 0,75\pi - 0,5\pi = 0,25\pi $$ Câu hỏi 6 : Một vật dao động điều hoà theo phương trình x = 3cos(
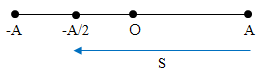
Đáp án: D Phương pháp giải: Lời giải chi tiết: Câu hỏi 7 : Một vật dao động điều hòa với chu kì T và biên độ A. Khi vật đi thẳng (theo một chiều) từ vị trí biên dương đến li độ - A/2 thì quãng đường của vật bằng:
Đáp án: C Phương pháp giải: Sử dụng lí thuyết về quãng đường đi được của vật dao động điều hoà Lời giải chi tiết: Quãng đường vật đi được: S = A + A/2 = 1,5A Câu hỏi 8 : Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 40cm. Trong mỗi chu kỳ dao động vật đi được quãng đường là:
Đáp án: C Phương pháp giải: Sử dụng lí thuyết về dao động điều hòa Lời giải chi tiết: Quỹ đạo chuyển động thẳng dài là l = 2A = 40 cm => biên độ dao động A = 20 cm Quãng đường vật đi được trong một chu kì là S = 4A = 4.20 = 80 cm => Chọn đáp án C Câu hỏi 9 : Một chất điểm dao động điều hòa có phương trình \(x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}\). Gọi v và a lần lượt là vận tốc và gia tốc của vật. Đặt \(m = {1 \over {{\omega ^2}}}\). Hệ thức đúng là:
Đáp án: D Phương pháp giải: Áp dụng hệ thức độc lập \({\left( {{v \over {\omega A}}} \right)^2} + {\left( {{a \over {{\omega ^2}A}}} \right)^2} = 1\) Lời giải chi tiết: + Với hai đại lượng vuông pha, ta có: \({\left( {{v \over {\omega A}}} \right)^2} + {\left( {{a \over {{\omega ^2}A}}} \right)^2} = 1 = > m{{{v^2}} \over {{A^2}}} + {m^2}{{{a^2}} \over {{A^2}}} = 1 = > {A^2} = ({v^2} + m{a^2})\) Câu hỏi 10 : Phương trình tọa độ của một chất điểm M dao động điều hòa có dạng x = - 6cos(10t) cm. Li độ của M khi pha dao động là \(\left( { - {\pi \over 3}} \right)\) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B + Li độ của M: \(x = - 6\cos \left( { - {\pi \over 3}} \right) = - 3\) Câu hỏi 11 : Hai dao động điều hòa có phương trình lần lượt là \({x_1} = {A_1}\cos \left( {\omega t} \right)\) cm và \({x_2} = - {A_2}\cos \left( {\omega t} \right)\)cm. Phát biểu nào sau đây là đúng?
Đáp án: A Phương pháp giải: Phương pháp : Đại cương về dao động điều hòa Lời giải chi tiết: Đáp án A + Hai dao động này ngược pha nhau. Câu hỏi 12 : Cho hai dao động điều hòa có phương trình lần lượt x1 = 2cos(ωt) cm, x2 = 4cos(ωt + π) cm. Ở thời điểm bất kì, ta luôn có:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Với hai đại lượng ngược pha ta luôn có \({{{x_1}} \over {{x_2}}} = {{{v_1}} \over {{v_2}}} = - {{{A_1}} \over {{A_2}}} = - {1 \over 2}\) Câu hỏi 13 : Vật dao động điều hoà với biên độ A = 5cm, tần số f = 4Hz. Tốc độ của vật khi có li độ x = 3cm là:
Đáp án: C Phương pháp giải: Áp dụng công thức độc lập với thới gian trong dao động điều hòa Lời giải chi tiết: Ta có \(v = \omega \sqrt {{A^2} - {x^2}} = 2\pi f\sqrt {{A^2} - {x^2}} = 8\pi \sqrt {{5^2} - {3^2}} = 32\pi \left( {cm/s} \right)\) Chọn đáp án C Câu hỏi 14 : Một chất điểm dao động điều hòa trên trục Ox có phương trình x = 8cos(πt + π/2) cm. Pha dao động của chất điểm khi t = 1s là
Đáp án: D Phương pháp giải: Pha dao động là đại lượng xác định trạng thái dao động và được xác định theo công thức ωt+φ Lời giải chi tiết: Thay t = 1s vào biểu thức tính pha dao động ta được kết quả π.1 + π/2 = 1,5π rad Chọn đáp án D Câu hỏi 15 : Trong dao động điều hoà, lúc li độ của vật có giá trị \(x = {{A\sqrt 3 } \over 2}cm\) thì độ lớn vận tốc là
Đáp án: A Phương pháp giải: Áp dụng công thức độc lập với thời gian \({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}}\) Lời giải chi tiết: Ta có \({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}} \Rightarrow v = \omega \sqrt {{A^2} - {x^2}} = \omega \sqrt {{A^2} - {{{A^2}.3} \over 4}} = {{\omega A} \over 2} = {{{v_{\max }}} \over 2}\) Chọn đáp án A
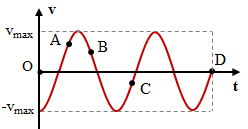
Câu hỏi 16 : Một vật dao động điều hòa có đồ thị vận tốc theo thời gian như hình vẽ. nhận định nào sau đây đúng ?
Đáp án: C Phương pháp giải: Từ đồ thị ta thấy A và B là hai điểm có cùng vận tốc, nhưng ở hai phía so với vận tốc cực đại, nên đó sẽ là hai điểm cách đều vị trí cân bằng và ở hai phía so với O. Tại C, vật có vận tốc âm và đang giảm về 0 nên vật đang từ vị trí cân bằng đi về biên âm. Nên tại C lực hồi phục có hướng ngược với vận tốc. Tại D vật có vận tốc bằng 0 nên vật đang ở vị trí biên. Vì vận tốc tại D là 0 và đang tăng nên D là vị trí biên âm Lời giải chi tiết: Từ đồ thị ta thấy A và B là hai điểm có cùng vận tốc, nhưng ở hai phía so với vận tốc cực đại, nên đó sẽ là hai điểm cách đều vị trí cân bằng và ở hai phía so với O. Tại C, vật có vận tốc âm và đang giảm về 0 nên vật đang từ vị trí cân bằng đi về biên âm. Nên tại C lực hồi phục có hướng ngược với vận tốc. Tại D vật có vận tốc bằng 0 nên vật đang ở vị trí biên. Vì vận tốc tại D là 0 và đang tăng nên D là vị trí biên âm Câu hỏi 17 : Một chất điểm dao động điều hòa với tần số bằng 4Hz và biên độ dao động 10cm. Độ lớn gia tốc cực đại của chất điểm bằng
Đáp án: B Phương pháp giải: Áp dụng công thức gia tốc cực đại: a0 = A.ω2 = A.(2πf)2 Lời giải chi tiết: Áp dụng công thức: a0 = A.ω2 = A.(2πf)2 = 10.(2π.4)2 = 6310 cm/s2 = 63,1 m/s2 Chọn B Câu hỏi 18 : Một chất điểm dao động điều hòa, gia tốc a và li độ x của chất điểm liên hệ với nhau theo hệ thức a = -16π2x (cm/s2). Chu kì của dao động bằng
Đáp án: B Phương pháp giải: Áp dụng công thức a = -ω2x. Chu kì được xác định bởi T = 2π/ ω Lời giải chi tiết: Vì a = -16π2x nên ta có ω = 4π (rad/s) Vậy T = 0,5s Chọn B Câu hỏi 19 : Phương trình vận tốc của một vật dao động điều hoà là \(\text{v = 120 cos20t (cm/s)}\), với t đo bằng giây. Vào thời điểm t = \(\frac{\text{T}}{\text{6}}\) (T là chu kì dao động), vật có li độ là
Đáp án: C Phương pháp giải: Từ phương trình vận tốc, xác định phương trình li độ của vật, sau đó thay giá trị của t vào phương trình. Lời giải chi tiết: Ta có: \(\text{v = 120 cos20t (cm/s)}\Rightarrow \text{x = }\int{\text{vdt}}=\text{120}\text{.sin20t}\text{.}\frac{\text{1}}{\text{20}}=\text{6 sin20t = 6 cos(20t}-\frac{\pi }{2})\) Vào thời điểm \(\text{t = }\frac{\text{T}}{\text{6}}\), vật có li độ: \(\text{x = 6 cos(20}\text{.}\frac{1}{6}.\frac{2\text{ }\!\!\pi\!\!\text{ }}{20}-\frac{\pi }{2})=3\sqrt{3}\) (cm) Chọn C Câu hỏi 20 : Một vật nhỏ dao động điều hòa theo phương trình: x = Acos10t (cm), (t tính bằng s). Tại t = 2 s, pha của dao động là:
Đáp án: D Phương pháp giải: Phương trình li độ của dao động điều hòa: \(x = A\cos \left( {\omega t + \varphi } \right)\). Trong đó: A là biên độ; \(\omega \) là tần số góc; \(\varphi \) là pha ban đầu; \(\left( {\omega t + \varphi } \right)\)là pha dao động. Lời giải chi tiết: Phương trình dao động: x = Acos10t (cm). Tại t = 2 s, pha dao động 10t = 10.2 = 20 (rad). Chọn D. Câu hỏi 21 : Một vật nhỏ dao động theo phương trình \(x = 4\cos \left( {\omega t - \frac{\pi }{3}} \right)\) cm. Gọi T là chu kì dao động của vật. Pha của vật dao động tại thời điểm \(t = \frac{T}{3}\) là:
Đáp án: D Phương pháp giải: Phương trình li độ của dao động điều hòa: \(x = A\cos \left( {\omega t + \varphi } \right)\). Trong đó: là tần số góc; \(\varphi \) là pha ban đầu; \(\left( {\omega t + \varphi } \right)\)là pha dao động. Chu kì dao động: \(T=\frac{2\pi }{\omega }\). Lời giải chi tiết: Phương trình dao động: \(x = 4\cos \left( {\omega t - \frac{\pi }{3}} \right)\). Pha dao động của vật: \(\left( {\omega t - \frac{\pi }{3}} \right)\). Tại thời điểm \(t=\frac{T}{3}\Rightarrow \omega t-\frac{\pi }{3}=\omega .\frac{T}{3}-\frac{\pi }{3}=\frac{\omega .2\pi }{3\omega }-\frac{\pi }{3}=\frac{\pi }{3}\). Chọn D. Câu hỏi 22 : Hai dao động có phương trình lần lượt là: x1 = 5 cos (2πt + 0,75π) (cm) và x2 = 10 cos (2πt + 0,5π) (cm). Độ lệch pha của hai dao động này có độ lớn bằng
Đáp án: A Phương pháp giải: Độ lệch pha của hai dao động: \(\Delta \varphi = \left| {{\varphi _2} - {\varphi _1}} \right|\). Lời giải chi tiết: Pha ban đầu của hai dao động lần lượt là: \({\varphi _1} = 0,75\pi ;\,\,{\varphi _2} = 0,5\pi \) \(\Rightarrow \Delta \varphi =\left| {{\varphi }_{2}}-{{\varphi }_{1}} \right|=\left| 0,75\pi -0,5\pi \right|=0,25\pi \) Chọn A. Câu hỏi 23 : Một chất điểm dao động điều hòa trên trục Ox có phương trình \(x = 10cos\left( {\pi t - \dfrac{\pi }{2}} \right)\) (x tính bằng cm, t tính bằng s) thì
Đáp án: D Phương pháp giải: Vận dụng lí thuyết về dao động điều hòa Lời giải chi tiết: A – sai vì vận tốc của chất điểm tại VTCB là \({v_{max}} = A\omega = 10\pi \left( {cm/s} \right)\) B – sai vì chu kì dao dộng là \(T = 2s\) C – sai vì biên độ \(A = 10cm\) D - đúng Chọn D Câu hỏi 24 : Một vật dao động điều hòa trên trục Ox có phương trình dao động \(x = 5cos\left( {\pi t + 0,5\pi } \right)cm\) (với \(t\) tính bằng s). Tại thời điểm \(t = 1s\), pha dao động của vật là
Đáp án: C Phương pháp giải: Pha dao động tại thời điểm t: \(\omega t + \varphi \) Lời giải chi tiết: Pha của dao động tại thời điểm \(t = 1s\) là: \(\pi .1 + 0,5\pi = 1,5\pi \left( {rad} \right)\) Chọn C Câu hỏi 25 : Con lắc lò xo gồm vật nhỏ gắn với lò xo nhẹ dao động điều hòa theo phương ngang. Lực kéo về tác dụng vào vật luôn
Đáp án: A Phương pháp giải: Sử dụng lí thuyết về lực kéo về Lời giải chi tiết: Lực kéo về tác dụng vào vật luôn hướng về vị trí cân bằng Chọn A Câu hỏi 26 : Một vật dao động điều hòa dọc theo trục Ox, quanh vị trí cân bằng O với biên độ A và chu kỳ T. Trong khoảng thời gian \(\dfrac{T}{4}\), quãng đường lớn nhất mà vật có thể đi được là
Đáp án: A Phương pháp giải: Quãng đường lớn nhất vật đi được trong khoảng thời gian \(t < \dfrac{T}{2}\): \({S_{\max }} = 2A\sin \dfrac{{\Delta \varphi }}{2}\) Góc quay của vecto quay trong thời gian t: \(\Delta \varphi = \omega t = \dfrac{{2\pi }}{T}.t\) Lời giải chi tiết: Trong khoảng thời gian \(\dfrac{T}{4}\), vecto quay được góc: \(\Delta \varphi = \dfrac{{2\pi }}{T}.t = \dfrac{{2\pi }}{T}.\dfrac{T}{4} = \dfrac{\pi }{2}\,\,\left( {rad} \right)\) Quãng đường lớn nhất vật đi được trong khoảng thời gian \(\dfrac{T}{4}\) là: \({S_{\max }} = 2A\sin \dfrac{{\Delta \varphi }}{2} = 2A.\sin \dfrac{\pi }{4} = A\sqrt 2 \) Chọn A. Câu hỏi 27 : Một chất điểm dao động điều hòa trên trục Ox, gốc tọa độ O tại vị trí cân bằng. Phương trình vận tốc của vật là \(v = 20\pi \cos \left( {4\pi t + \dfrac{\pi }{6}} \right)\left( {cm{\rm{/}}s} \right)\). Phương trình dao động của vật có dạng
Đáp án: C Phương pháp giải: Vận tốc cực đại: \({v_{\max }} = \omega A\) Vận tốc luôn sớm pha hơn li độ góc \(\dfrac{\pi }{2}\) Lời giải chi tiết: Từ phương trình vận tốc của vật: \(v = 20\pi \cos \left( {4\pi t + \dfrac{\pi }{6}} \right)\,\,\left( {cm/s} \right)\), ta có: \({v_{\max }} = \omega A \Rightarrow A = \dfrac{{{v_{\max }}}}{\omega } = \dfrac{{20\pi }}{{4\pi }} = 5\,\,\left( {cm} \right)\) Tần số góc: \(\omega = 4\pi \,\,\left( {rad/s} \right)\) Vận tốc luôn sớm pha hơn li độ góc \(\dfrac{\pi }{2}\left( {rad} \right)\) \({\varphi _{v/x}} = \dfrac{\pi }{2} = {\varphi _v} - {\varphi _x} \Rightarrow {\varphi _x} = {\varphi _v} - {\varphi _{v/x}} = \dfrac{\pi }{6} - \dfrac{\pi }{2} = - \dfrac{\pi }{3}\,\,\left( {rad} \right)\) Vậy phương trình dao động là: \(x = 5\cos \left( {4\pi t - \dfrac{\pi }{3}} \right)\,\,\left( {cm} \right)\) Chọn C. Câu hỏi 28 : Một chất điểm chuyển động tròn đều trên đường tròn tâm O bán kính 10cm với tốc độ góc 5rad/s. Hình chiếu của chất điểm lên trục Ox nằm trong mặt phẳng quỹ đạo có tốc độ cực đại là
Đáp án: B Phương pháp giải: Sử dụng biểu thức tính tốc độ cực đại của vật dao động điều hòa: \({v_{max}} = A\omega \) Lời giải chi tiết: Tốc độ cực đại của chất điểm: \({v_{max}} = A\omega = 10.5 = 50\left( {cm/s} \right)\) Chọn B Câu hỏi 29 : Một vật dao động điều hòa với chu kì 2s, biên độ 10cm. Chọn gốc tọa độ tại vị trí cân bằng của vật. Khi vật cách vị trí cân bằng 6cm thì tốc độ của nó là
Đáp án: C Phương pháp giải: Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết: Tần số góc của dao động: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \left( {rad/s} \right)\) Áp dụng hệ thức độc lập, ta có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) \( \Rightarrow v = \omega \sqrt {{A^2} - {x^2}} = \pi \sqrt {{{10}^2} - {6^2}} = 8\pi cm/s = 25,13m/s\) Chọn C Câu hỏi 30 : Một vật dao động điều hòa có vận tốc cực đại bằng \(6cm/s\) và gia tốc cực đại bằng \(18cm/{s^2}\). Tần số dao động của vật là:
Đáp án: C Phương pháp giải: Vận tốc cực đại và gia tốc cực đại trong dao động điều hòa : \(\left\{ \begin{array}{l} Công thức tính tần số dao động: \(f = \frac{\omega }{{2\pi }}\) Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l} Tần số dao động của vật: \(f = \frac{\omega }{{2\pi }} = \frac{3}{{2\pi }} = 0,48Hz\) Chọn C. Câu hỏi 31 : Một chất điểm dao động quanh vị trí cân bằng với phương trình li độ \(x = 2.\cos \left( {2\pi t + \frac{\pi }{2}} \right)\) (x đo bằng cm; t đo bằng s). Tại thời điểm t = 0,25s chất điểm có li độ bằng:
Đáp án: C Phương pháp giải: Thay giá trị t vào biểu thức x Lời giải chi tiết: Tại t = 0,25s chất điểm có li độ bằng: \(x = 2.\cos \left( {2\pi .0,25 + \frac{\pi }{2}} \right) = - 2cm\) Chọn C. Câu hỏi 32 : Vật dao động điều hòa với phương trình x = 5cos(4 πt + π/6) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian
Đáp án: A Phương pháp giải: Áp dụng công thức tính quãng đường lớn nhất. $${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\omega \Delta t} \over 2}$$ Lời giải chi tiết: Đáp án: A Quãng đường lớn nhất vật đi được trong khoảng thời gian $${T \over 6}$$ là: $${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\omega \Delta t} \over 2} = 2{\rm{Asin}}{{\omega {T \over 6}} \over 2} = 2{\rm{Asin}}{{{{2\pi } \over T}{T \over 6}} \over 2} = 2{\rm{Asin}}{\pi \over 6} = A = 5cm$$ Câu hỏi 33 : Vật dao động điều hòa với phương trình x = 5cos(4πt + π/6) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian
Đáp án: C Phương pháp giải: Áp dụng công thức tính quãng đường lớn nhất. $${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\Delta \varphi } \over 2} = 2{\rm{Asin}}{{\omega \Delta t} \over 2}$$ Lời giải chi tiết: Ta có: $$\Delta \varphi = \Delta t.\omega = {T \over 3}{{2\pi } \over T} = {{2\pi } \over 3}$$ Quãng đường lớn nhất vật đi được trong khoảng thời gian $${T \over 3}$$ là: $${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\Delta \varphi } \over 2} = 2{\rm{Asin}}{{{{2\pi } \over 3}} \over 2} = 2{\rm{Asin}}{\pi \over 3} = A\sqrt 3 = 5\sqrt 3 cm$$ =>Chọn C Câu hỏi 34 : Một vật dao động điều hòa với biên độ A. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian 2T/3.
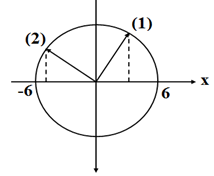
Đáp án: B Phương pháp giải: Áp dụng công thức tính quãng đường lớn nhất. $${S_{{\rm{max}}}} = 2{\rm{Asin}}{{\Delta \varphi } \over 2} = 2{\rm{Asin}}{{\omega \Delta t} \over 2}$$ Lời giải chi tiết: Ta có: $$\Delta \varphi = \Delta t.\omega = {{2T} \over 3}{{2\pi } \over T} = {{4\pi } \over 3} = \pi + {\pi \over 3}$$ Quãng đường lớn nhất vật đi được trong khoảng thời gian $${T \over 3}$$ là: $${S_{{\rm{max}}}} = {S_{(\pi )}} + {S_{({\pi \over 3})}} = 2A + 2{\rm{Asin}}{{\Delta \varphi } \over 2} = 2A + 2{\rm{Asin}}{{{\pi \over 3}} \over 2} = 3A$$ =>Chọn B
Câu hỏi 35 : Một vật dao động điều hoà với phương trình x = 4cos(4πt + π/3). Tính quãng đường lớn nhất mà vật đi được trong khoảng thời gian Dt = 1/6 (s).
Đáp án: D Phương pháp giải: Lời giải chi tiết:
=> => S max = 2A.sin Câu hỏi 36 :
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Phương pháp: Sử dụng vòng tròn lượng giác Chu kỳ dao động của vật: T = 0,2s. Biểu diễn trên hình vẽ vị trí (1) là vị trí của vật ở thời điểm t1 , sau t = 0,05s = T/4 vật ở vị trí (2) có \(x = - 3\sqrt 3 ;v < 0\) Câu hỏi 37 : Một vật dao động điều hòa với biên độ A=12cm và chu kì T=0,4s. Tốc độ trung bình lớn nhất của vật trong khoảng thời gian 1/15s là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Phương pháp : Áp dụng công thức tính tốc độ trung bình \(\Delta t = {1 \over {15}} = {T \over 6}\) Để tốc độ trung bình lớn nhất thì quãng đường đi được lớn nhất và bằng A = 12cm. \({v_{tb}} = {{12} \over {1/15}} = 180cm/s\) Câu hỏi 38 : Một chất điểm dao động điều hòa với chu kì T. Gọi vTB là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà
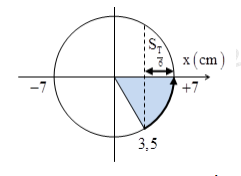
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 39 : Một chất điểm dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Tốc độ trung bình của chất điểm từ thời điểm t0 chất điểm qua vị trí có li độ 3,5 cm theo chiều dương đến thời điểm gia tốc của chất điểm có độ lớn cực đại lần thứ 3 (kể từ t0) là
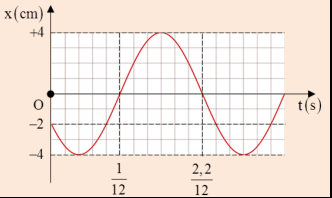
Đáp án: C Phương pháp giải: Áp dụng công thức tính tốc độ trung bình của chất điểm dao động điều hoà. Lời giải chi tiết: Quỹ đạo chuyển động 14cm => Biên độ dao động A = 7cm Chu kỳ T = 1s Từ đường tròng lượng giác ta thấy: Gia tốc của chất điểm có độ lớn cực đại khi chất điểm ở vị trí biên. Trong một chu kì chất điểm đi qua vị trí biên 2 lần, do vậy thời gian để chất điểm đi từ vị trí ban đầu đến khi gia tốc có độ lớn cực tiểu lần thứ 3 sẽ là: \(t = T + \frac{T}{6}\) Vậy vận tốc trung bình của vật là: \({v_{tb}} = \frac{s}{t} = \frac{{{s_T} + {s_{\frac{T}{6}}}}}{{T + \frac{T}{6}}} = \frac{{4.7 + \frac{7}{2}}}{{1 + \frac{1}{6}}} = 27cm/s\) Câu hỏi 40 : Hình vẽ là đồ thi biễu diễn độ dời của dao động x theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Từ đồ thị ta thấy: \({T \over 2} = {{2,2} \over {12}} - {1 \over {12}} = {{1,2} \over {12}} \Rightarrow T = 0,2s \Rightarrow \omega = {{2\pi } \over T} = 10\pi \left( {rad/s} \right)\) Tại thời điểm t = 0: \(\eqalign{
|













 s.
s. (s) =>
(s) =>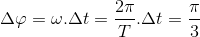 (rad)
(rad)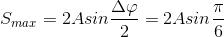 = A = 5 cm
= A = 5 cm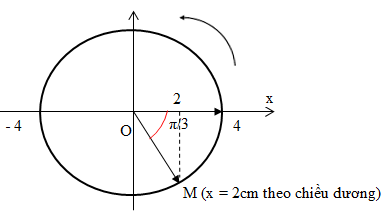
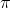 t +
t + 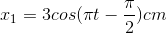 ;
;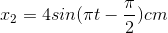 ;
;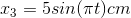 . Kết luận nào sau đây là đúng ?
. Kết luận nào sau đây là đúng ?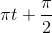 ) cm, pha dao động của chất điểm tại thời điểm t = 1s.
) cm, pha dao động của chất điểm tại thời điểm t = 1s.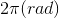
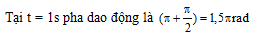
 :
: :
: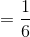 (s)
(s)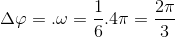
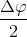 = 2A.sin
= 2A.sin 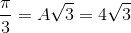 cm
cm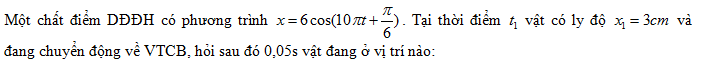
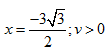
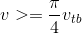 là
là