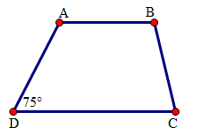
20 bài tập cơ bản Hình thang, hình thang cânLàm bàiCâu hỏi 1 : Góc kề cạnh bên của hình thang có số đo là \({70^0}\) . Góc kề còn lại của cạnh bên đó là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Có \(\widehat {ADC} = {70^0}\) như hình vẽ. Cần tính \(\widehat {DAB}\) Ta có: \(AB//CD(gt)\) nên \(\widehat {jAD} = \widehat {ADC} = {70^0}\) ( hai góc so le trong) Góc \(\widehat {jAD}\) và \(\widehat {DAB}\) là hai góc kề bù nên \(\widehat {DAB} = {180^0} - \widehat {jAD} = {180^0} - {70^0} = {110^0}\)
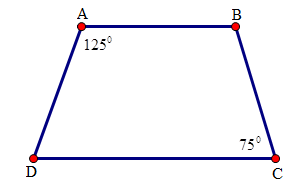
Chọn B. Câu hỏi 2 : Một hình thang có cặp góc đối là \({125^0}\) và \({75^0}\), cặp góc đối còn lại của hình thang đó là:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Cách 1: Tổng số đo cặp góc đối còn lại của hình thang là : \({360^0} - \left( {{{125}^0} + {{75}^0}} \right) = {160^0}\) Ta thấy \({105^0} + {55^0} = {160^0}\) . Do đó cặp góc đối còn lại của hình thang đó là \({105^0};{55^0}\) . Chọn A. Cách 2: Vì \(AB//CD\) nên: \(\widehat D + \widehat A = {180^0}\) (hai góc trong cùng phía) \( \Rightarrow \widehat D = {180^0} - \widehat A = {180^0} - {125^0} = {55^0}\). \(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía) \( \Rightarrow \widehat B = {180^0} - \widehat C = {180^0} - {75^0} = {105^0}\). Chọn A. Câu hỏi 3 : Các góc của tứ giác có thể là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Tổng các góc trong 1 tứ giác bằng \(360^0\). Các góc của tứ giác có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng \(360^0\) . Các trường hợp còn lại không thỏa mãn định lí tổng các góc trong tam giác. Chọn C. Câu hỏi 4 : Cho tứ giác ABCD, trong đó \(\widehat{A\,\,}+\widehat{B\,\,}=140{}^\circ \) .Tổng \(\widehat{C\,\,}+\widehat{D\,\,}=?\)
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn: Trong tứ giác ABCD có: \(\widehat{\,C\,\,}+\widehat{\,D\,\,}=360{}^\circ -\left( \widehat{A\,\,}+\widehat{\,B\,\,} \right)=360{}^\circ -140{}^\circ =220{}^\circ \) Chọn A Câu hỏi 5 : Chọn câu đúng nhất trong các câu sau khi định nghĩa tứ giác ABCD:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn: Theo định nghĩa: Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng. Chọn B. Câu hỏi 6 : Cho hình thang \(ABCD\) có \(\widehat A = {60^0};\widehat B = {60^0};\widehat C = {120^0}\) . Số đo góc \(D\) bằng:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết
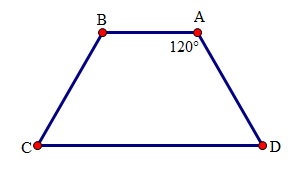
Xét hình thang \(ABCD\) có \(\widehat A = \widehat B = {60^0}\) nên \(ABCD\) là hình thang cân. Do đó \(\widehat D = \widehat C = {120^0}\) Chọn C Câu hỏi 7 : Cho hình thang cân \(ABCD(AB//CD)\). Cho \(\widehat A = {120^0 }\) thì
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết
Do \(ABCD\) là hình thang cân có đáy \(AB\) nên \(\widehat{A}=\widehat{B}={{120}^{0}}\) . Vậy \(\widehat{B}={{120}^{0}}\) Chọn A Câu hỏi 8 : Tứ giác có 2 cạnh đối song song và 2 đường chéo bằng nhau là:
Đáp án: B Phương pháp giải: Dựa vào dấu hiệu nhận biết hình thang cân. Lời giải chi tiết: Tứ giác có 2 cạnh đối song song là hình thang. Lại thêm có 2 đường chéo bằng nhau nên tứ giác đó là hình thang cân. Chọn B Câu hỏi 9 : Tổng các góc của hình thang cân là bao nhiêu:
Đáp án: B Phương pháp giải: Áp dụng định lý: Tổng bốn góc của một tứ giác bằng \(360^\circ .\) Lời giải chi tiết: Tổng các góc của một hình thang cân là \({360^0}.\) Chọn B. Câu hỏi 10 : Nếu một hình thang có 2 cạnh bên bằng nhau, 2 đường chéo bằng nhau thì đó là:
Đáp án: B Phương pháp giải: Áp dụng tính chất: Trong hình thang cân có 2 cạnh bên bằng nhau, 2 đường chéo bằng nhau Lời giải chi tiết: Nếu hình thang có 2 cạnh bên bằng nhau và 2 đường chéo bằng nhau thì thì hình thang đó là hình thang cân. (dhnb) Chọn B. Câu hỏi 11 : Số đo các góc của hình thang \(ABCD\) theo tỉ lệ: \(\hat A:\hat B:\hat C:\hat D = 4:3:2:1\). Số đo các góc theo thứ tự đó là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Theo tính chất của dãy tỉ số bằng nhau và tổng các góc của tứ giác ta có: \(\dfrac{{\hat A}}{4} = \dfrac{{\hat B}}{3} = \dfrac{{\hat C}}{2} = \dfrac{{\hat D}}{1} = \dfrac{{\hat A + \hat B + \hat C + \hat D}}{{4 + 3 + 2 + 1}} = \dfrac{{{{360}^0}}}{{10}} = {36^0}\) Do đó: \(\hat A = {144^0};\hat B = {108^0};\hat C = {72^0};\hat D = {36^0}\) Chọn C. Câu hỏi 12 : Câu nào sau đây là đúng khi nói về hình thang:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Theo định nghĩa: Hình thang là tứ giác có hai cạnh đối song song. Chọn A. Câu hỏi 13 : Hình thang \(ABCD\) có \(\hat D = {80^0},\hat B = {50^0},\hat C = {100^0}\) . Số đo góc \(\widehat A\) là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Trong hình thang \(ABCD\) có: \(\hat A = {360^0} - \left( {\hat B + \hat C + \hat D} \right) = {360^0} - \left( {{{80}^0} + {{50}^0} + {{100}^0}} \right) = {130^0}\) Chọn B. Câu hỏi 14 : Góc kề cạnh 1 bên hình thang có số đo 750, góc kề còn lại của cạnh bên đó là:
Đáp án: C Phương pháp giải: Ta sử dụng tính chất của hình thang: Ta thấy góc A và D là hai góc trong cùng phía nên \(\widehat A + \widehat D = {180^0}\) từ đó ta suy ra số đo góc A. Lời giải chi tiết: Ta có: \(\widehat A + \widehat D = {180^0}\) \(\eqalign{ & \Rightarrow \widehat A = {180^0} - \widehat D \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {75^0} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = {105^0} \cr} \) Chọn C Câu hỏi 15 : Số đo các góc của tứ giác ABCD theo tỉ lệ: \(\widehat{A\,\,}:\widehat{B\,\,}:\widehat{C\,\,}:\widehat{D\,\,}=4:3:2:1\) . Số đo các góc theo thứ tự đó là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Hướng dẫn: Theo tính chất của dãy tỉ số bằng nhau và tổng các góc của tứ giác ta có: \(\frac{\widehat{A\,\,}}{4}=\frac{\widehat{B\,}}{3}=\frac{\widehat{C\,}}{2}=\frac{\widehat{D\,\,}}{1}=\frac{\widehat{A\,\,}+\widehat{B\,}+\widehat{C\,\,}+\widehat{D\,\,}}{4+3+2+1}=\frac{360{}^\circ }{10}=36{}^\circ \) Do đó: \(\widehat{A\,\,}=144{}^\circ ;\,\,\widehat{B\,\,}=108{}^\circ ;\,\,\widehat{C\,\,}=72{}^\circ ;\,\,\widehat{D\,\,}=36{}^\circ \) Chọn C Câu hỏi 16 : Tứ giác ABCD có \(\widehat{A\,\,}=65{}^\circ ~;\,\,\widehat{B\,\,}=117{}^\circ ;\,\,\widehat{C}=71{}^\circ \) . Khi đó \(\widehat{D\,\,}=?\)
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn: Trong tứ giác ABCD có: \(\widehat{D\,\,}=360{}^\circ -\left( \widehat{A\,\,}+\widehat{B\,\,}+\widehat{C\,\,} \right)=360{}^\circ -\left( 65{}^\circ +117{}^\circ +71{}^\circ \right)=107{}^\circ \) Chọn B Câu hỏi 17 : Cho tứ giác ABCD, có\(\hat A = {80^0},\hat B = {120^0},\hat D = {50^0},\) Số đo \(\hat C\) là:
Đáp án: C Phương pháp giải: Dựa vào tính chất tổng các góc của một tứ giác bằng \({360^0}\) Lời giải chi tiết: Xét tứ giác ABCD ta có:\(\hat A + \widehat B + \widehat C + \widehat D = {360^0}\) \(\eqalign{& \Rightarrow \widehat C = {360^0} - \left( {\hat A + \widehat B + \widehat D} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - \left( {{{80}^0} + {{120}^0} + {{50}^0}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {250^0} = {110^0}. \cr} \) Chọn C Câu hỏi 18 : Chọn phương án đúng:
Đáp án: B Phương pháp giải: Áp dụng định nghĩa: Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau. Lời giải chi tiết: +) Đáp án A sai vì Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau. \( \Rightarrow \) Đáp án B đúng. Chọn B. Câu hỏi 19 : Nếu hình thang có 2 cạnh bên song song thì:
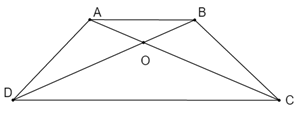
Đáp án: C Phương pháp giải: Áp dụng tính chất: hình thang có 2 cạnh bên song song thì 2 cạnh bên bằng nhau và 2 cạnh đáy bằng nhau. Lời giải chi tiết: Nếu hình thang có 2 cạnh bên song song thì 2 cạnh bên bằng nhau và 2 cạnh đáy bằng nhau. Chọn C. Câu hỏi 20 : Cho hình thang cân ABCD có AB //CD, O là giao điểm của AC và BD. Chứng minh rằng OA = OB, OC = OD. Phương pháp giải: Áp dụng các dấu hiệu nhận biết của hình thang cân: + Có 2 góc kề một đáy bằng nhau \(\left( {\angle {\rm{DAB}} = \angle {\rm{ABC}}} \right)\) + Có 2 đường chéo bằng nhau \(\left( {AD = BC} \right)\) Lời giải chi tiết: Xét \(\Delta ABD\) và \(\Delta BAC\) ta có: \(\begin{array}{l}AB\,\,chung\\AD = BC\,\,\,\left( {tc} \right)\\BD = AC\,\,\left( {tc} \right)\\ \Rightarrow \Delta ABD = \Delta BAC\,\,\,\left( {c - c - c} \right)\end{array}\) \( \Rightarrow \left\{ \begin{array}{l}\angle ADB = \angle ACB\\\angle ABD = \angle BAC\end{array} \right.\) (các cặp góc tương ứng). Xét \(\Delta AOB\) ta có: \(\angle ABD = \angle BAD\,\,\,\left( {cmt} \right)\) hay \(\angle ABO = \angle BAO\) \( \Rightarrow \Delta ABO\) cân tại \(O\) (định nghĩa). \( \Rightarrow AO = OB\) (tính chất). Ta có: \(\left\{ \begin{array}{l}AC = AO + OC\\BD = BO + OD\end{array} \right.\) Mà \(BD = AC\) (hai đường chéo của hình thang cân) \( \Rightarrow OD = OC\) (theo tính chất bắc cầu).
|