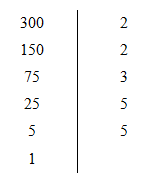Phương pháp giải:

- Thực hiện phép tính để tìm ra .

- Áp dụng kiến thức ước của 1  số.

- Liệt kê tất cả các ước của số đó.

Lời giải chi tiết:

Ta có \(a = {2^2}.7 = 4.7 = 28\)

\(28 = 28.1 = 14.2 = 7.4 = 7.2.2\).

Vậy \({\rm{U}}\left( {28} \right){\rm{ = }}\left\{ {{\rm{1;2;4;7;14;28}}} \right\}\)

Phương pháp giải:

- Phân tích số ra thành số nguyên tố.

Lời giải chi tiết:

- Đáp án A sai vì 1 không phải là số nguyên tố; 15 = 3.5

- Đáp án B sai vì đây là phép cộng.

- Đáp án C đúng vì 3  và  5 là  2 số nguyên số có tích là 15

- Đáp án D sai vì đây là phép cộng.

Chọn C.

Phương pháp giải:

- Phân tích số 140  thành tích các thừa số nguyên tố.

Lời giải chi tiết:

Ta có \(140 = {2^2}.5.7 = {a^2}.b.7\) nên a =2 .

Chọn B.

Phương pháp giải:

- Áp dụng kiến thức: nếu số a phân tích thành thừa số nguyên tố với\(a = {x^m}.{y^n}\), trong đó x và y là số nguyên tố thì số lượng các ước của số a là:\((m + 1).(n + 1)\)

Lời giải chi tiết:

Ta có \({\rm{225 = }}{{\rm{3}}^2}{\rm{.}}{{\rm{5}}^2}\).

Vậy \(a = 225;\,m = 2;\,n = 2\)

Vậy số lượng ước của số 225  là \((2 + 1).(2 + 1) = 3.3 = 9\)

Chọn D.

Phương pháp giải:

- Phân tích  1 số thành thừa số nguyên tố.

Lời giải chi tiết:

- Ta có:

\(\eqalign{& \matrix{ \matrix{50 \hfill \cr 25 \hfill \cr 5 \hfill \cr}  & \matrix{2 \hfill \cr 5 \hfill \cr  5 \hfill \cr}   \cr }   \cr & 1 \cr} \)

\(\matrix{\matrix{69 \hfill \cr 23 \hfill \cr 1 \hfill \cr}  & \matrix{3 \hfill \cr 23 \hfill \cr \hfill \cr}   \cr } \)

\(\matrix{\matrix{1554 \hfill \cr 777 \hfill \cr 111 \hfill \cr 37 \hfill \cr 1 \hfill \cr}  & \matrix{2 \hfill \cr 7 \hfill \cr 3 \hfill \cr 37 \hfill \cr \hfill \cr}   \cr  } \)

vậy \(50 = {2.5^2}\)

\(69 = 3.23\)

\(1554 = 2.7.3.37 = 2.3.7.37\)

Phương pháp giải:

- Phân tích số 240 ra thừa số nguyên tố.

- Đếm số lượng thừa số.

Lời giải chi tiết:

\(\matrix{ \matrix{ 240 \hfill \cr 120 \hfill \cr 60 \hfill \cr 30 \hfill \cr 15 \hfill \cr 5 \hfill \cr 1 \hfill \cr}  & \matrix{ 2 \hfill \cr 2 \hfill \cr  2 \hfill \cr 2 \hfill \cr 3 \hfill \cr 5 \hfill \cr \hfill \cr}   \cr  } \)

Vậy\(240 = 2.2.2.2.3.5 = {2^4}.3.5\)nên số lượng số nguyên tố là 3 .

Phương pháp giải:

- Áp dụng kiến thức ước số. (vì số kẹo chia hết cho 2;3;4  nên 2;3;4 là ước của số kẹo)

- Áp dụng kiến thức tích các thừa số nguyên tố.

Lời giải chi tiết:

Lần 1  cô chia cho  2 bạn, 2 bạn có số kẹo như nhau:\({\rm{a}} \vdots {\rm{2}}\)

Lần  2 cô chia cho 3  bạn, 3 bạn có số kẹo như nhau:\({\rm{a}} \vdots {\rm{3}}\)

Lần  3 cô chia cho  4 bạn, 4 bạn có số kẹo như nhau:\({\rm{a}} \vdots {\rm{4}}\)

Do \({\rm{4}} \vdots {\rm{2}}\) nên nếu a chia hết cho 4  thì a cũng chia hết cho 2.

Vậy \(a = {3^n}{.4^p}\).  Để cô giáo có số kẹo nhỏ nhất thì  là số nhỏ nhất nên n = p =1 .

Vậy cô giáo có số kẹo là: 3.4 = 12 (cái kẹo)

Phương pháp giải:

- Phân tích  1 số thành thừa số nguyên tố.

- Áp dụng: 2 số 1  và 0  không phải là số nguyên tố.

Lời giải chi tiết:

a) Ta có: 

\(\matrix{\matrix{270 \hfill \cr 135 \hfill \cr 45 \hfill \cr 15 \hfill \cr 5 \hfill \cr 1 \hfill \cr}  & \matrix{2 \hfill \cr 3 \hfill \cr 3 \hfill \cr 3 \hfill \cr 5 \hfill \cr \hfill \cr}   \cr } \)

Do đó\(270 = {2.3^3}.5\)

Vậy phép phân tích trên là đúng.

b)  Phép phân tích \(84 = {1.2^2}.21\) là sai vì 1;21  không phải là số nguyên tố.

- Sửa lại:

\(\matrix{\matrix{84 \hfill \cr 42 \hfill \cr 21 \hfill \cr 7 \hfill \cr 1 \hfill \cr}  & \matrix{2 \hfill \cr 2 \hfill \cr 3 \hfill \cr 7 \hfill \cr \hfill \cr}   \cr } \)

Vậy \(84 = {2^2}.3.7\)

c) 

Phép phân tích 459 = 27.17 là sai vì 27 không phải là số nguyên tố.

- Sửa lại:

\(\matrix{\matrix{459 \hfill \cr 153 \hfill \cr 51 \hfill \cr 17 \hfill \cr 1 \hfill \cr}  & \matrix{3 \hfill \cr 3 \hfill \cr 3 \hfill \cr 17 \hfill \cr  \hfill \cr}   \cr } \)

Vậy \(459 = 3.3.3.17 = {3^3}.17\)

Phương pháp giải:

- Áp dụng phân tích 1  số thành thừa số nguyên tố.

- Sử dụng kiến thức:

Nếu \(m = {a^x}\) thì x + 1 có  ước

Nếu \(m = {a^x}.{b^y}\) thì (x + 1).(y + 1) có  ước

Nếu \(m = {a^x}.{b^y}.{c^z}\)thì \((x + 1).(y + 1).(z + 1)\) có  ước

Lời giải chi tiết:

- Số \(64 = {2^6}\), vậy số ước là 6 + 1 = 7

- Số\(144 = {2^4}{.3^2}\), vậy số ước là\((4 + 1).(2 + 1) = 5.3 = 15\)

Phương pháp giải:

- Viết số 50 dưới dạng tích hai số tự nhiên.

- Kiểm tra các cặp số tìm được, cặp nào có tổng lớn nhất chính là hai số cần tìm.

Lời giải chi tiết:

Ta có:\(50 = 1.50 = 2.25 = 5.10\) nên hai số tự nhiên cần tìm có thể là: 1 và 50; 2 và 25; 5 và 10.

Lại có: 

\(\eqalign{& 1 + 50 = 51  \cr & 2 + 25 = 27  \cr & 5 + 10 = 15 \cr} \)

Nên hai số tự nhiên có tổng lớn nhất là 1 và 50.

Vậy hai số cần tìm là 1 và 50.

Phương pháp giải:

- Áp dụng kiến thức về phân tích   số thành thừa số nguyên tố (các thừa số trong tích phải là số nguyên tố)

Lời giải chi tiết:

Khi phân tích một số \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\) ra thừa số nguyên tố thì các số \({p_1};\,{p_2};...;\,{p_k}\) phải là các số nguyên tố.

Phương pháp giải:

Áp dụng định nghĩa: phân tích một số nguyên tô lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Có thể áp dụng cách phân tích các số ra thừa số nguyên tố “theo cột dọc”.

Lời giải chi tiết:

Phân tích các số đã cho ra thừa số nguyên tố ta có:

\(\begin{array}{l}84 = {2^2}.3.7\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,340 = {2^2}.5.17\\92 = 2.2.23\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,228 = {2^2}.3.19\end{array}\)

Vậy  phân tích đúng là \(228 = {2^2}.3.19\)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Ta có: \(84 = {2^2}.3.7.\)

Chọn A.

Phương pháp giải:

Có thể phân tích một số ra thừa số nguyên tố theo cột dọc.

Vậy \(300 = {2^2}{.3.5^2}\).

Chọn D.

Lời giải chi tiết:

Ta có thể phân tích số \(300\) ra thừa số nguyên tố “theo cột dọc” như sau:

Phương pháp giải:

+) Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:

                        Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ

+) Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc: \((\,\,)\,\, \to {\rm{[}}\,\,{\rm{]}}\,\, \to {\rm{\{ }}\,\,{\rm{\} }}\) 

+) \(\left| a \right| = a\) nếu \(a \ge 0\) và \(\left| a \right| =  - a\) nếu \(a < 0\)

Lời giải chi tiết:

\(\begin{array}{l}1)\,\,a)\,\,\left( {3.5.7 - 18:6} \right)\,\,.\,\,12\\\,\,\,\,\,\,\, = \left( {15.7 - 3} \right)\,\,.\,\,12\\\,\,\,\,\,\,\, = \left( {105 - 3} \right)\,\,.\,\,12\\\,\,\,\,\,\,\, = 102\,\,.\,\,12\\\,\,\,\,\,\,\, = 1224\end{array}\)                                                   \(\begin{array}{l}b){\rm{ }}\left| {2018} \right|--\left| {--1} \right| + \left| 0 \right|\\ = 2018--1 + 0\\ = 2017 + 0\\ = \,\,\,\,\,2017\\\end{array}\)                            

\(\begin{array}{l}2)\;\;{6^2}:4\,.\,3 + {2.5^2}\\ = 36:4\,.\,3 + 2.25\\ = 9\,.\,3 + 50\\ = 27 + 50\\ = 77\end{array}\)

Phân tích kết quả ra thừa số nguyên tố ta có: \(77 = 7.11\)

Chọn A