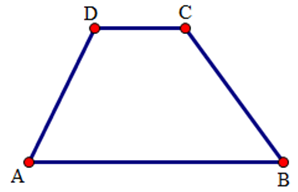
15 bài tập tổng hợp Ôn tập chương 1: Tứ giácLàm bàiCâu hỏi 1 : Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14cm. Viết GT-KL và tính độ dài MI, IK. Phương pháp giải: + Dựa vào tính chất đường trung bình của tam giác để tính độ dài MI, MK. Từ đó suy ra độ dài IK. Lời giải chi tiết: - Hình thang ABCD có: AM=MD(gt)BN=NC(gt)}⇒ MN là đường trung bình MN//AB//CD (tính chất). - Tam giác ACD có: AM=MDMI//AB}⇒ ID = IB (định lý đảo về đường trung bình của tam giác). MI là đường trung bình của ∆ADC ⇒MI=12AB=12.6=3(cm) - Tương tự tam giác ACD có: AM = MD, MK//DC nên AK = KC, MK là đường trung bình, ta có: MK=12CD=12.14=7(cm) IK = MK - MI = 7 - 3 = 4(cm) Câu hỏi 2 : Cho tứ giác ABCD có ˆA=600,ˆB=800,ˆC=1000 a) Tính số đo góc D? b) Tứ giác ABCD là hình gì? Vì sao? Phương pháp giải: + Áp dụng tính chất tổng các góc của tứ giác + Dựa vào tính chất hình thag để chứng minh tứ giác ABCD là hình thang. Lời giải chi tiết: a) Xét tứ giác ABCD có: ˆA+ˆB+ˆC+ˆD=3600⇒ˆD=3600−(ˆA+ˆB+ˆC)=3600−(600+800+1000)=1200 b) Xét tứ giác ABCD có:ˆA+ˆD=600+1200=1800. Mà hai góc này ở vị trí trong cùng phía, do đó AB // CD. Suy ra tứ giác ABCD là hình thang.
Câu hỏi 3 : Cho biết ABCD=57 và đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10 cm. Tính độ dài các đoạn thẳng AB, CD?
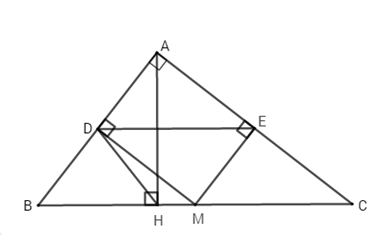
Đáp án: C Phương pháp giải: - Áp dụng lý thuyết về tỉ số đoạn thẳng để thực hiện yêu cầu bài toán. Lời giải chi tiết: Theo bài ra, ta có: ABCD=57 ⇒AB=57CD Mà đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10 cm, suy ra: CD−AB=10. ⇒CD−57CD=10⇔27CD=10⇔CD=10.72=35 cm⇒AB=57CD=57.35=25 cm Chọn C. Câu hỏi 4 : Cho ΔABC vuông tại A (AB < AC) có M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E. a) Chứng minh tứ giác ADME là hình chữ nhật b) Chứng minh E là trung điểm cuả đoạn thẳng AC và tứ giác CMDE là hình bình hành c) Vẽ AH⊥BC. Chứng minh tứ giác MHDE là hình thang cân Phương pháp giải: a) Chứng minh 1 tứ giác là hình chữ nhật dựa vào dấu hiệu tứ giác có 3 góc vuông. b) Sử dụng định lí về đường trung bình của tam giác để suy ra trung điểm cạnh còn lại. Chứng minh 1 tứ giác là có 2 cạnh đối song song là hình bình hành. c) Chứng minh 1 tứ giác là hình thang cân dựa ào dấu hiệu hình bình hành có 2 góc kề 1 đáy bằng nhau.
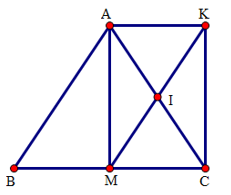
Lời giải chi tiết: a) Chứng minh tứ giác ADME là hình chữ nhật. Ta có: ∧A=900(vì ΔABC vuông tại A) ^MDA=90∘(do MD⊥AB) ^MEA=90∘(do ME⊥AC) Do đó tứ giác ADME là hình chữ nhật. (dấu hiệu nhận biết) b) Chứng minh E là trung điểm cuả đoạn thẳng AC và tứ giác CMDE là hình bình hành. Ta có {ME⊥ACBA⊥AC⇒ME//BA(1) Mà M là trung điểm của BC (gt) (2) Từ (1) và (2) suy ra E cũng là trung điểm của AC. (định lý đảo của đường trung bình). Lại có : Tứ giác CMDE là hình chữ nhật nên MD//AE⇒MD//AC(3) Mà M là trung điểm của BC (gt) (4) Từ (3) và (4) suy ra D là trung điểm của AB. Do đó DE là đường trung bình của tam giác ABC ⇒DE//BC⇒DE//MC(5) Mặt khác {CA⊥ABHD⊥AB⇒CA//HD⇒CE//HD(6) Từ (5) và (6) suy ra tứ giác DECM là hình bình hành. (dấu hiệu nhận biết). c) Chứng minh tương tự ta có tứ giác DEMB cũng là hình bình hành⇒ˆB=^DEM(7) Tam giác BHA vuông có HD là trung tuyến ⇒HD=DA=DB=AB2 Suy ra DH=DB hay ΔHBDcân tại D ⇒ˆB=^DHB Mà ^DHB=^HDE(vì DE//BC) Nên ˆB=^HDE(8) Từ (7) và (8) suy ra ^DEM=^HDE(9). Xét tứ giác HMED có HM//DE nên tứ giác HMDE là hình thang (10) Từ (9) và (10) suy ra tứ giác HMED là hình thang cân. Câu hỏi 5 : Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. a) Tứ giác AMCK là hình gì? Vì sao? b) Tứ giác AKMB là hình gì? Vì sao? c) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông? Phương pháp giải: + Chứng minh AKCM là hình chữ nhật dựa vào dấu hiệu hình bình hành có một góc vuông. + Chứng minh AKCM là hình bình hành dựa vào dấu hiệu tứ giác có một cặp cạnh song song và bằng nhau. + Để AMCK là hình vuông ta dựa vào dấu hiệu hình chữ nhật có hai cạnh bên bằng nhau là hình vuông, từ đó suy ra điều kiện của tam giác ABC. Lời giải chi tiết: a) ΔABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao ⇒AM⊥BC⇒^AMC=900. (1) Xét tứ giác AMCK có: AC cắt MK tại I, mà AI = IC, MI = IK (gt)a) ABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao (1) ⇒ Tứ giác AMCK là hình bình hành (dấu hiệu nhận biết) (2) Từ (1) và (2) suy ra AMCK là hình chữ nhật (dấu hiệu nhận biết). b) Tứ giác AMCK là hình chữ nhật (c/m a) ⇒ AK // CM ⇒AK // BM (3) mà AK = MC (AMCK là hình chữ nhật) và MC = MB (gt) ⇒ AK = BM (4) Từ (3) và (4) Tứ giác AKMB là hình bình hành. (dấu hiệu nhận biết) c) Để tứ giác AMCK là hình vuông thì AM = MC Mà AM là đường trung tuyến của tam giác cân ABC ⇒AM=MC=12BC⇒ Tam giác ABC vuông cân tại A.
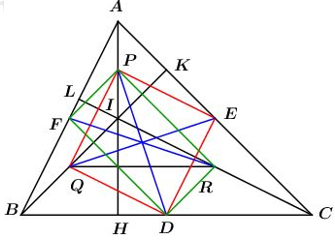
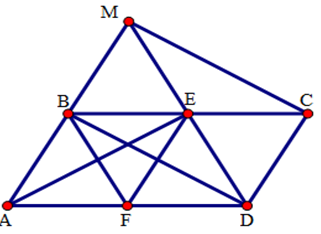
Câu hỏi 6 : Cho ΔABC có 3 góc nhọn, đường cao AH, BK, CL cắt nhau tại I. Gọi D, E, F là trung điểm của BC, CA, AB. Gọi P, Q, R là trung điểm của IA, IB, IC. a) Chứng minh: PFDR, PEDQ là hình chữ nhật. b) Chứng minh: PD, QE, RF cắt nhau tại trung điểm của mỗi đoạn thẳng. Phương pháp giải: a) Dựa vào định lý đường trung bình của tam giác để chứng minh được các cạnh PR = DF và PR//DF⇒PFDR là hình bình hành theo dấu hiệu nhận biết. Lại có PF//BK;BK⊥AC;AC//PR nên PF⊥PR nên PFDR là hình chữ nhật. Chứng minh tương tự với tứ giác PQDE. b) Dựa vào tính chất hình chữ nhật: Hai đường chéo cắt nhau tại trung điểm mỗi đường để suy ra điều phải chứng minh. Lời giải chi tiết: a) Xét ΔABI có FA=FB(gt);PI=PA(gt)⇒FP là đường trung bình của ΔABI ⇒FP//BI(t/c)⇒FP//BK Mà BK⊥AC(gt) nên FP⊥AC(1) Xét ΔAIC có PA=PI(gt);RI=RC(gt)⇒PR là đường trung bình của tam giác ⇒PR//AC;PR=12AC(t/c)(2) Từ (1) và (2) suy ra FP⊥PR (từ vuông góc đến song song) Xét ΔABC có FB=FA(gt);DB=DC(gt)⇒DF là đường trung bình của tam giác Từ (2) và (3) ta có PR//DF;PR=DF nên PRDF là hình bình hành. Lại có PF//BK;BK⊥AC;AC//PR nên PF⊥PR nên hình bình hành là hình chữ nhật. Chứng minh tương tự ta cũng có: {PE//CLCL⊥ABAB//PQ⇒PE⊥PQ và PQ//DE//AB;PQ=DE=12AB nên PEDQ là hình bình hành. Do đó PEDQ là hình chữ nhật. b) PEDQ là hình chữ nhật nên PD cắt EQ tại trung điểm O của PD và EQ Lại có PFDR là hình chữ nhật nên PD cắt FR tại trung điểm O của pD và FR Do đó O là trung điểm các đoạn thẳng PD,FR,EQ Vậy ba đường thẳng PD,FR,EQ cắt nhau tại trung điểm của mỗi đoạn.
Câu hỏi 7 : Cho hình bình hành ABCD có AD = 2AB, ˆA=600. Gọi E, F lần lượt là trung điểm BC và AD. a) Chứng minh AE ⊥ BF. b) Chứng minh tứ giác BFDC là hình thang cân. c) Lấy M đối xứng của A qua B. Chứng minh tứ giác BMCD là hình chữ nhật. Suy ra M, E, D thẳng hàng. Phương pháp giải: a. Để chứng minh AE⊥BF ta chứng minh ABEF là hình thoi dựa vào dấu hiệu hình bình hành có hai cạnh kề bằng nhau. b. Để chứng minh BFDC là hinh thang cân ta dựa vào dấu hiệu hình thang có hai cạnh bên bằng nhau. c. Để chứng minh BMCD là hình chữ nhật ta dựa vào dấu hiệu hình bình hành có một góc vuông. Lời giải chi tiết:
a) Do E là trung điểm của BC nên BE=EC=12BC F là trung điểm của AD nên AF=FD=12AD Mà AD = BC (do ABCD là hình bình hành), nên BE = AF. (1) Ta lại có BE // AF (do ABCD là hình bình hành) (2) Từ (1) và (2) suy ra ABEF là hình bình hành. (3) Ta có AD=2AB⇒AB=12AD⇒AB=BE (4) Từ (3) và (4) suy ra ABEF là hình thoi, suy ra AE⊥BF (hình thoi có hai đường chéo vuông góc). b) Xét tam giác ABF có: AB = AF nên tam giác ABF cân tại A. Lại có ∠A=600, suy ra tam giác ABF là tam giác đều ⇒{BF=AB=AF∠ABF=600 (tính chất tam giác đều) Ta có: ∠A=600⇒∠BCD=600 (tính chất hình bình hành) Vì ∠A+∠ABC=1800 (hai góc trong cùng phía) ⇒∠ABC=1800−∠A=1200.⇒∠FBC=∠ABC−∠ABF=1200−600=600⇒∠FBC=∠BCD=600. Xét tứ giác FDBC có: FD // BC (do ABCD là hình bình hành) ∠FBC=∠BCD=600(cmt) Suy ra BFDC là hình thang cân. (dhnb). c) Xét tứ giác BMCD có BM = CD (= AB), BM // CD nên tứ giác BMCD là hình bình hành (5) Xét tam giác ABD có: BF=AF=FD=12AD Suy ra tam giác ABD vuông tại B. Suy ra ^MBD=900(6) Từ (5) và 6 suy ra BMCD là hình chữ nhật. Có E là trung điểm của BC ⇒ E là giao điểm của hai đường chéo hình chữ nhật. ⇒ M, E, D thẳng hàng.
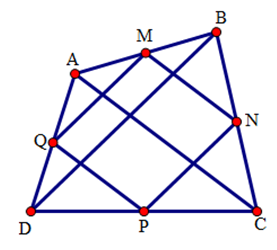
Câu hỏi 8 : Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Hai đường chéo AC và BD phải thỏa mãn điều kiện gì để M, N, P, Q là bốn đỉnh của: a) Hình chữ nhật? b) Hình thoi? c) Hình vuông? Phương pháp giải: Dựa vào dấu hiệu nhận biết các hình: +) Hình chữ nhật, hình thoi, hình vuông để tìm ra điều kiện của hai đường chéo AC và BD tương ứng. Lời giải chi tiết: Xét tam giác ABD có: M là trung điểm của AB (gt) Q là trung điểm của AD (gt) ⇒ QM là đường trung bình của tam giác ABD. (định lý) Do đó QM // BD và QM=12BD (1) CM tương tự ta cũng có NP là đường trung bình của tam giác BCD. ⇒{NP//BDNP=12BD(2) Từ (1) và (2) ta suy ra MNPQ là hình bình hành (dấu hiệu nhận biết). a) Để MNPQ là hình chữ nhật ⇔MN⊥NP⇔AC⊥BD (vì MN // AC, NP // BD) Điều kiện cần tìm là hai đường chéo BD và AC vuông góc với nhau. b) Để MNPQ là hình thoi ⇔MN=NP⇔AC=BD (vì MN=12AC,NP=12BD) Điều kiện cần tìm là hai đường chéo BD và AC bằng nhau. c) Để MNPQ là hình vuông ⇔{MN⊥PQMN=PQ⇔{AC⊥BDAC=BD Điều kiện cần tìm là hai đường chéo BD và AC bằng nhau và vuông góc với nhau. Câu hỏi 9 : Cho ΔABC vuông tại A (AB<AC). Gọi M,N,K thứ tự là trung điểm của AB,AC và BC a) Chứng minh KN=12AB và ABKN là hình thang vuông. b) Qua M kẻ đường thẳng song song với BN , cắt tia KN tại Q . Chứng minh AKCQ là hình thoi. c) MN cắt BQ tại O , AK cắt BN tại I . Biết BC=24cm . Tính độ dài OI .
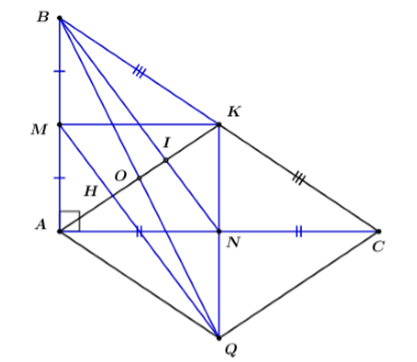
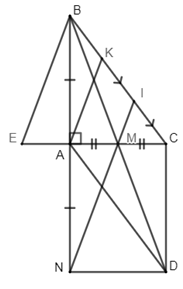
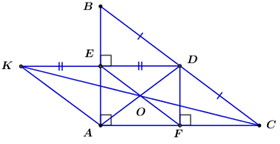
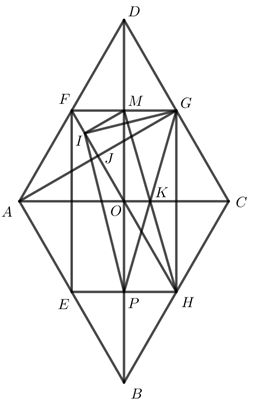
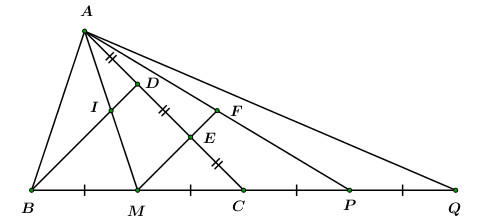
Đáp án: B Phương pháp giải: - Áp dụng tính chất đường trung bình của tam giác, dấu hiệu nhận biết hình bình hành, hình thoi, tính chất hình bình hành, tính chất trung điểm. Lời giải chi tiết: a) Vì N,K lần lượt là trung điểm của AC và BC (gt) ⇒NK là đường trung bình của ΔACB (dấu hiệu nhận biết đường trung bình của tam giác) ⇒{NK=AB2(∗)NK//AB (tính chất đường trung bình của tam giác) Ta có: NK//AB(cmt)⇒ tứ giác NKBA là hình thang (dấu hiệu nhận biết hình thang) Lại có: ∠NAB=900(gt)⇒ hình thang NKBA là hình thang vuông (dấu hiệu nhận biết hình thang vuông) b) Ta có: AB//NK(cmt)⇒QN//MB mà QM//NB(gt)⇒ tứ giác MBNQ là hình bình hành (dấu hiệu nhận biết hình bình hành) ⇒QN=MB=AB2(∗∗) (tính chất hình bình hành) Từ (∗) và (∗∗)⇒QN=NK lại có AN=NC(gt)⇒AQCK là hình bình hành (dấu hiệu nhận biết hình bình hành) Mặt khác, xét ΔvABC có AK là trung tuyến (gt) suy ra AK=BC2 (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) Mà KC=BC2(gt)⇒AK=CK ⇒ hình bình hành AQCK là hình thoi (dấu hiệu nhận biết hình thoi) c) Gọi H là giao điểm của MQ và AK Vì BNQM là hình bình hành (cmt) ⇒{BN//MQBO=OQ (tính chất hình bình hành) ⇒∠IBO=∠OQH (so le trong) Xét ΔOIB và ΔOHQ có: ∠IBO=∠OQH (cmt) BO=OQ(cmt) ∠BOI=∠HOQ (đối đỉnh) ⇒ΔOIB=ΔOHQ(g−c−g)⇒OI=OH (2 cạnh tương ứng) Xét ΔIAB có: MH//IB (do MQ//BN) M là trung điểm của AB(gt) ⇒ H là trung điểm của AI (trong tam giác, đường thẳng đi qua trung điểm của cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba) ⇒AH=HI(1) (tính chất trung điểm của đoạn thẳng) Vì AKCQ là hình thoi (cmt) mà N là trung điểm của AC(gt) và AC∩KQ={N}⇒N là trung điểm của AC (tính chất hình thoi) Xét ΔKCQ có: IN//HQ (do MQ//BN) N là trung điểm của KQ(cmt) ⇒I là trung điểm của HK (trong tam giác, đường thẳng đi qua trung điểm của cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba) ⇒KI=HI(2) (tính chất trung điểm của đoạn thẳng) Từ (1) và (2)⇒AH=HI=IK=13AK Xét ΔvABC có: AK=BC2=12cm (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) ⇒AH=HI=IK=13AK=123=4cm Ta có: NK//AB(cmt)⇒KQ//AB(3) Do AKCQ là hình thoi (cmt) và N là giao điểm của hai đường chéo AC và KQ⇒KN=12KQ (tính chất hình thoi) Mà KN=12AB(cmt)⇒KQ=AB(4) Từ (3) và (4)⇒ABKQ là hình bình hành (dấu hiệu nhận biết hình bình hành) ⇒O là trung điểm của AK (tính chất hình bình hành) ⇒AO=OK (tính chất trung điểm) Lại có {OI=OK−KIOH=OA−AH Mà AH=IK (cmt)⇒OI=OH=IH2=42=2 cm Chọn B Câu hỏi 10 : Cho ΔABC vuông tại A , gọi M là trung điểm của AC . Gọi D là điểm đối xứng với B qua M . a. Chứng minh tứ giác ABCD là hình bình hành. b. Gọi N là điểm đối xứng với B qua A . Chứng minh tứ giác ACDN là hình chữ nhật. c. Kéo dài MN cắt BC tại I . Vẽ đường thẳng qua A song song với MN cắt BC ở K . Chứng minh: KC=2BK d. Qua B kẻ đường thẳng song song với MN cắt AC kéo dài tại E . Tam giác ABC cần có thêm điều kiện gì để tứ giác EBMN là hình vuông. Phương pháp giải: Áp dụng dấu hiệu nhận biết các hình: hình bình hành, hình chữ nhật, hình thoi. Áp dụng tính chất: đường trung bình của tam giác, của hình thang. Lời giải chi tiết: a. Ta có: Vì D và B đối xứng với nhau qua M (gt) ⇒MD=MB(tính chất hai điểm đối xứng với nhau qua 1 điểm) Xét tứ giác ABCD ta có: {MC=MA(gt)MD=MB(cmt) ⇒ Tứ giác ABCD là hình bình hành (dhnb) b. Vì N đối xứng với B qua A (gt) ⇒NA=AB(tính chất) Lại có ABCD là hình bình hành (cmt) ⇒{DC=ABDC//AB(tính chất) ⇒{DC=ANDC//AN ⇒ANDC là hình bình hành (dhnb) Mặt khác, ∠CAB=900(gt)⇒∠CAN=900 ⇒ hình bình hành ANDC là hình chữ nhật (dhnb) (đpcm) c. Xét ΔBNI có: AK//NI (do AK//MN ) NA=AB(gt) ⇒ AK là đường trung bình của ΔBNI(định lý) ⇒KI=KB (tính chất) Xét ΔCAK có: MI//AK (do AK//NI) MA=MC (gt) ⇒ MI là đường trung bình của ΔACK (dhnb) ⇒IK=CI (tính chất) Mà KC=CI+IK⇒KC=2KI=2KB (do KI=KB) d. Vì BE//MN(gt)⇒BE//IM⇒ Tứ giác BEMI là hình thang (dấu hiệu nhận biết hình thang) Lại có: K là trung điểm của BI (cmt) và AK//MI(cmt)⇒Alà trung điểm của EM (trong hình thang, nếu một đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì đi qua trung điểm của cạnh bên thứ hai) Xét tứ giác BENM có hai đường chéo BN và EM cắt nhau tại trung điểm A của mỗi đường. ⇒BENMlà hình bình hành (dhnb) Mà BN⊥EM(gt)⇒ hình bình hành BENM là hình thoi (dhnb) Để hình thoi BENM là hình vuông khi và chỉ khi AB=AM⇔AB=12AC. Câu hỏi 11 : Cho ΔABC vuông tại A , có D là trung điểm của BC . Gọi E,F lần lượt là hình chiếu của D trên AB và AC . 1. Chứng minh: AD=EF 2. Gọi K là điểm đối xứng với D qua E . Chứng minh ba đường thẳng AD,EF,KC đồng quy. Phương pháp giải: Áp dụng: - Dấu hiệu nhận biết hình chữ nhật - Tính chất: hình chữ nhật, đối xứng, từ vuông góc đến song song. Lời giải chi tiết: 1. Xét tứ giác AEDF có: ∠BAC=∠AED=∠AFD=900(gt)⇒AEDF là hình chữ nhật (dhnb) ⇒AD=EF (tính chất hình chữ nhật) 2. Gọi O là giao điểm của EF và AD⇒Olà trung điểm của EF và AD(tính chất hình chữ nhật) (1) ⇒OE=OF (tính chất trung điểm) Do D và K đối xứng nhau qua E nên suy ra {DK⊥ABED=KE (tính chất đối xứng) Mà AC⊥AB(gt)⇒DK//AC (từ vuông góc đến song song) Ta có: ED là đường trung bình của ΔABC (E, D là trung điểm của AB, BC (gt)) ⇒ED=12BC⇒BC=2ED. Xét tứ giác AKDC ta có: BC//KD(cmt)KD=BC(=2KD) ⇒AKDC là hình bình hành (dhnb) ⇒KC,EF cắt nhau tại trung điểm của mỗi đường (tính chất) Mà O là trung điểm của EF (cách gọi) ⇒KC,EF,AD đồng quy tại O. (đpcm) Câu hỏi 12 : Cho hình thoi ABCD có góc D bằng 60o. Gọi E, H, G, F lần lượt là trung điểm của AB, BC, CD và DA. a) Chứng minh tứ giác EFGH là hình chữ nhật. b) Cho AG cắt HF tại J. Chứng minh rằng HF=4FJ. c) Gọi I là trung điểm của FJ và P là giao điểm của EH và DB. Chứng minh IG vuông góc với IP. d) Cho AB=2cm. Tính độ dài IP. Phương pháp giải: a) Tứ giác có 3 góc vuông là hình chữ nhật. b) Áp dụng tính chất đường trung bình trong tam giác và hình thoi để chứng minh. c) Gọi FG cắt BD tại M ; PG cắt MH tại K. Chứng minh dựa vào định lý đường trung tuyến trong tam giác vuông ứng với cạnh huyền bằng nửa cạnh huyền và tam giác có đường trung tuyến ứng với cạnh bằng nửa cạnh đó là tam giác vuông. d) Tính các đoạn cần thiết dựa vào các đẳng thức đã chứng minh ở trên từ đó tính các cạnh của tam giác vuông PIG bằng cách sử dụng định lý Pytago. Lời giải chi tiết: Cho hình thoi ABCD có góc D bằng 60o. Gọi E, H, G, F lần lượt là trung điểm của AB, BC, CD và DA. a) Chứng minh tứ giác EFGH là hình chữ nhật. Ta có ABCD là hình thoi ⇒AC⊥BD (tính chất) (1) Có E, F lần lượt là trung điểm của AB và DA (gt) ⇒ EF là đường trung bình trong tam giác ABD ⇒EF // BD (2) Có F, G lần lượt là trung điểm của AD và CD (gt) ⇒ FG là đường trung bình trong tam giác DAC ⇒FG // AC (3) Từ (1), (2), (3) ⇒EF⊥FG (từ vuông góc đến song song) Tương tự ⇒FG⊥GH;GH⊥HE;HE⊥EF ⇒ EFGH là hình chữ nhật (dhnb) b) Cho AG cắt HF tại J. Chứng minh rằng HF=4FJ. Ta có F, H lần lượt là trung điểm của AD và BC ⇒ FH là đường trung bình của hình thoi ABCD ⇒FH // AB // CD và FH=AB=CD Xét tam giác ADG có F là trung điểm của AD, FJ // DG (FH // CD) ⇒J là trung điểm của AG ⇒ FJ là đường trung bình trong tam giác ADG ⇒FJ=12DG=14CD=14HF (do G là trung điểm của CD nên DG=12CD) ⇒HF=4FJ (đpcm) c) Gọi I là trung điểm của FJ và P là giao điểm của EH và DH. Chứng minh IG vuông góc với IP. Gọi AC cắt BD tại O ⇒DO=12BD;OC=OA=12AC (tính chất) Xét tam giác ACD có DA=DC (ABCD là hình thoi), ∠D=60o (gt) ⇒ΔACD đều (dhnb) ⇒AC=CD;DO=AG (tính chất) ⇒AG vừa là trung tuyến vừa là đường cao ⇒AG⊥CD⇒AG⊥HF (từ vuông góc đến song song) Gọi FG cắt BD tại M Xét tam giác ODA có F là trung điểm của AD, FM // OA (FG // AC) ⇒M là trung điểm của OD ⇒ FM là đường trung bình trong tam giác ODA ⇒FM=12OA Tương tự ta cũng được GM=12OC mà OA=OC (cmt) ⇒FM=GM ⇒ M là trung điểm của FG ⇒ IM là đường trung bình trong tam giác FJG ⇒ IM // AG mà AG⊥HF (cmt) ⇒IM⊥HF Gọi PG cắt MH tại K. Dễ thấy PHGM là hình chữ nhật (có 3 góc vuông) ⇒ K là trung điểm của PG và HM ; HM=PG Có tam giác IMH vuông tại I (IM⊥HF) có K là trung điểm của HM ⇒ KI=12HM=12PG ⇒ Tam giác PIG vuông tại I ⇒ IG⊥IP (đpcm) d) Cho AB=2cm. Tính độ dài IP. Ta có ABCD là hình thoi có HF là đường trung bình và ΔACD đều ⇒AB=BC=CD=DA=AC=HF=2cm ⇒AG=2√32=√3cm⇒GJ=12AG=√32cm (J là trung điểm của AG) OC=OA=12AC=1cm ; FG=EH=12AC=1cm OD=AG=√3cm⇒EF=GH=OD=12BD=√3cm IJ=12FJ=18HF=14cm ; PH=MG=12FG=12cm Áp dụng định lý Pytago cho tam giác GJI vuông tại J ta được: IG=√IJ2+GJ2=√116+34=√134(cm) Áp dụng định lý Pytago cho tam giác HPG vuông tại H ta được: PG=√PH2+GH2=√14+3=√132(cm) Áp dụng định lý Pytago cho tam giác PIG vuông tại I ta được: IP=√PG2−IG2=√134−1316=√394(cm) Câu hỏi 13 : Cho ABC là tam giác nhọn, có AM là đường trung tuyến. Trên cạnh AC lấy hai điểm D và E sao cho AD=DE=EC. AM cắt BD tại I. a) Chứng minh: tứ giác BDEM là hình thang. b) Chứng minh: I là trung điểm của AM. c) Chứng minh: BI=3DI d) Trên tia đối của tia CB lấy hai điểm P và Q sao choCP=PQ=CM . Chứng minh: ME,AP,DQ đồng quy tại một điểm. Phương pháp giải: a) Sử dụng tính chất đường trung bình, tứ giác có 2 cạnh đối song song là hình thang. b) Sử dụng tính chất bắc cầu c) Áp dụng tính chất đường trung bình. d) Chứng minh có một điểm đồng thời thuộc cả ba đường thẳng đó. DF≡DQ hay F thuộc DQ. Lời giải chi tiết:
a) Xét △CBD có M là trung điểm BC,E là trung điểm DC ⇒ME là đường trung bình của ⇒ME//BD;ME=12BD (tính chất đường trung bình) ⇒ Tứ giác BDEM là hình thang (tứ giác có 2 cạnh đối song song là hình thang). b) Ta có: ME//BD⇒ID//ME Mà D là trung điểm của AE ⇒I là trung điểm của AM c) Ta có: ID=12ME (tính chất đường trung bình) ⇒ID=12.12BD=14BD(ME=12BD(cmt)) BI=BD−DI=BD− 12BD= 34BD⇒BI=3ID d) Gọi F=ME∩AP Xét △AMP có AC là đường trung tuyến,AE=23AC⇒E là trọng tâm △AMP⇒EF=12ME EF//ID(doME//ID:cmt);ID=EF=12ME ⇒IDFE là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành) ⇒IE//DF(1) Ta có: (chứng minh trên); BP=34BQ ⇒IP//DQ (định lý Ta-let đảo trong tam giác) IP là đường trung tuyến trong △AMP⇒IP≡IE⇒IE//DQ(2) Từ (1) và (2) ⇒DF≡DQ hay F∈DQ Vậy ME,DQ,AP đồng quy tại F.
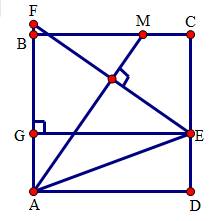
Câu hỏi 14 : Cho hình vuông ABCD, E là một điểm trên cạnh CD. Tia phân giác của góc BAE cắt BC tại M. Chứng minh rằng AM≤2ME Phương pháp giải: Ta thấy nếu vẽ EF⊥AM(F∈AB) thì EF = AM. Ta có AM là đường phân giác, đường cao của tam giác AEF, nên tam giác AEF cân đỉnh A. Từ đó có ME = MF. Xét ba điểm M, E, F ta có: EF≤ME+MF Do đó AM≤2ME Lời giải chi tiết: Vẽ EF⊥AM(F∈AB),EG⊥AB(G∈AB) Tứ giác AGED là hình chữ nhật( vì ˆG=ˆA=ˆD=900 ), suy ra GE = AD. Xét ΔGEF và ΔBAM có: ^EGF=^ABM=900; GE = AB (=CD); ^FEG=^MAB Do đó ΔGEF=ΔBAM (g.c.g) suy ra EF = AM. Tam giác AEF có AM là đường phân giác và là đường cao nên tam giác AEF cân đỉnh A. Ta có AM là đường trung trực của EF, nên ME = MF. Xét ba điểm M, E, F ta có: EF≤ME+MF⇔EF≤2ME. Do đó AM≤2ME (đpcm). Câu hỏi 15 : Cho tam giác ABC (^A<900). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG. Gọi M là trung điểm của đoạn thẳng DF. Chứng minh rằng tam giác MBC cân tại M. Phương pháp giải: + Vẽ thêm điểm H sao cho tam giác BHC vuông cân đỉnh B, H thuộc nửa mặt phẳng bờ BC có chứa điểm A. + Chứng minh M là trung điểm của HC để suy ra MB = MC. + Chứng minh MB vuông góc với MC để suy ra điều phải chứng minh. Lời giải chi tiết: Trên nửa mặt phẳng bờ BC có chưa A dựng tam giác BHC vuông cân đỉnh B. Xét tam giác BHD và tam giác BCA có: DB = BA (Vì ADBE là hình vuông) ^DBH=^ABC (vì cùng phụ với góc HBA) BH = BC (vì tam giác BHC vuông cân đỉnh B) Do đó: ΔBHD=ΔBCA(c.g.c), suy ra DH=AC,^BHD=^BCA. AC cắt HD tạ K, cắt BH tại I. Xét tam giác IHK và tam giác ICB có: ^HIK=^CIB (đối đỉnh), ^BHD=^BCA, do đó ^HKI=^IBC=900⇒KC⊥DH Mặt khác KC⊥CF, do đó DH // CF. Ta có DH = CF (= AC) và DH // CF nên DHFC là hình bình hành. Mà M là trung điểm của DF nên M là trung điểm của HC, suy ra tam giác MBC vuông cân đỉnh M.
|