15 bài tập cơ bản Đường trung bình của tam giác, của hình thangLàm bàiCâu hỏi 1 : Tam giác \(MNP\) có \(A,B\) thứ tự là trung điểm của \(NP,MN\). Biết \(AB=3dm\), khi đó:
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng tính chất của đường trung bình của tam giác: Độ dài đường trung bình của tam giác bằng một nửa cạnh đáy Lời giải chi tiết: Hướng dẫn giải chi tiết Xét tam giác \(MNP\) có: \(A\) là trung điểm của \(NP\) \(B\) là trung điểm của \(MN\) \(\Rightarrow AB\) là đường trung bình của tam giác MNP. \(\Rightarrow AB=\frac{MP}{2}\Rightarrow MP=2.AB=2.3=6\left( dm \right)\) Chọn A Câu hỏi 2 : Cho tam giác \(ABC\) và điểm \(M\) là trung điểm của \(AB\). Đường song song với \(BC\) kẻ từ \(M\) cắt \(AC\) tại \(N\) . Cho \(MN=12cm\) thì \(BC\) bằng:
Đáp án: B Phương pháp giải: Phương pháp: Sử dụng tính chất của đường trung bình của tam giác: Độ dài đường trung bình của tam giác bằng một nửa cạnh đáy Lời giải chi tiết: Hướng dẫn giải chi tiết Xét tam giác \(ABC\) có: \(\left. \begin{align} & MA=MB\left( gt \right) \\ & MN//BC \\\end{align} \right\}\Rightarrow NA=NC\) Do đó \(MN\) là đường trung bình của tam giác \(ABC\). \(\Rightarrow MN=\frac{BC}{2}\Rightarrow BC=2MN=2.12=24cm\) Chọn B Câu hỏi 3 : Trong các câu sau, chọn câu sai:
Đáp án: B Phương pháp giải: Phương pháp: Dựa vào định nghĩa, định lí đường trung bình của hình thang Lời giải chi tiết: Cách giải: Theo định lí đường trung bình của hình thang thì độ dài đường trung bình của hình thang bằng nửa tổng hai đáy của hình thang. Do đó câu: “ Độ dài đường trung bình của hình thang bằng nửa hiệu hai đáy” là sai. Các câu còn lại đúng vì thỏa mãn định nghĩa, định lí đường trung bình của hình thang. Chọn B. Câu hỏi 4 : Cho hình thang \(ABCD\) có \(AB,\text{ }AD\) là hai đáy; \(I\) và \(K\) là lần lượt là trung điểm của \(AD\) và \(BC\) ; \(IK\) được gọi là gì của hình thang \(ABCD\) .
Đáp án: A Phương pháp giải: Phương pháp: Dựa vào định nghĩa đường trung bình của hình thang Lời giải chi tiết: Cách giải: Xét hình thang \(ABCD\) có: \(I\) là trung điểm cạnh \(AD\) \(K\) là trung điểm cạnh \(BC\) \(\Rightarrow \) \(IK\) là đường trung bình của hình thang \(ABCD\) ( đn) Chọn A. Câu hỏi 5 : Chọn câu đúng. Đường trung bình của hình thang có \(2\) đáy là \(4\)cm và \(6\)cm có độ dài là:
Đáp án: B Phương pháp giải: Sử dụng kiến thức đường trung bình của hình thang bằng nửa tổng 2 đáy. Lời giải chi tiết: Đường trung bình của hình thang có độ dài là: \((4 + 6):2 = 5cm\). Chọn B. Câu hỏi 6 : Chọn phát biểu đúng:
Đáp án: A Phương pháp giải: Áp dụng định nghĩa đường trung bình của hình thang: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. Lời giải chi tiết: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. Hình thang có duy nhất 1 đường trung bình. Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng hai đáy. Chọn A. Câu hỏi 7 : Đường trung bình của tam giác:
Đáp án: B Phương pháp giải: Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy Lời giải chi tiết: + Đáp án A sai vì đoạn thẳng nối 2 điểm bất kì của tam giác không thể khẳng định ngay là đường trung bình. +) Đáp án B: Đường trung bình của tam giác là đoạn thẳng cắt hai cạnh của tam giác, song song với cạnh thứ ba và bằng nửa cạnh ấy. \( \Rightarrow \) Đáp án B đúng. Chọn B. Câu hỏi 8 : Cho tam giác đều \(ABC\) cạnh bằng \(4\). Lấy điểm \(D\) trên \(AB\) với \(AD=2\). Đường song song với \(BC\) kẻ từ \(D\) cắt \(AC\) tại \(E\) thì :
Đáp án: C Phương pháp giải: Phương pháp: - Sử dụng tính chất hình thang có hai góc kề một đáy bằng nhau là hình thang cân để chứng minh BDEC là hình thang cân. - Sử dụng tính chất: Đường trung bình của tam giác bằng một nửa cạnh đáy để tính độ dài đường trung bình từ đó tính được chu vi hình thang cân \(BDEC\). Lời giải chi tiết: Hướng dẫn giải chi tiết Xét tam giác \(ABC\) có: \(D\) là trung điểm của \(AB,DE//BC\) suy ra \(E\) là trung điểm của \(AC\) nên \(DE\) là đường trung bình của tam giác \(ABC\). Do đó \(EC=\frac{AC}{2}=2\left( cm \right);DE=\frac{BC}{2}=\frac{4}{2}=2\left( cm \right)\) Suy ra \(BD=EC\left( =2cm \right)\) Xét tứ giác BDEC có: \(DE//BC\left( gt \right)\) \(\widehat{B}=\widehat{C}={{60}^{0}}\left( gt \right)\) Suy ra \(BDEC\) là hình thang cân. Chu vi \(BDEC=BD+DE+EC+BC=2+2+2+4=10\left( cm \right)\) Chọn C
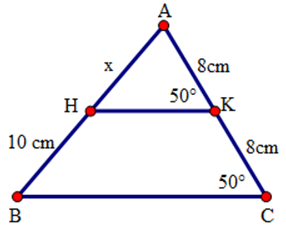
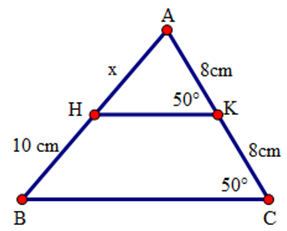
Câu hỏi 9 : Cho hình sau. Giá trị của x là:
Đáp án: D Phương pháp giải: Phương pháp: Sử dụng định lý: Đường thẳng đi qua trung điểm cạnh thứ nhất và song song với cạnh thứ hai của tam giác thì đi qua trung điểm cạnh thứ ba của tam giác. Lời giải chi tiết: Hướng dẫn giải chi tiết Ta có \(\widehat{AKH}=\widehat{ACB}={{50}^{0}}\), mà hai góc này ở vị trí đồng vị nên \(HK//BC\). Xét tam giác \(ABC\) có \(K\) là trung điểm của \(AC,HK//BC\) nên \(H\) là trung điểm của \(AB\), do đó \(HA=HB=10cm\). Chọn D Câu hỏi 10 : Một hình thang có độ dài hai đáy là \(3cm\) và \(7cm\) thì đường trung bình của hình thang có độ dài là:
Đáp án: D Phương pháp giải: Phương pháp: Sử dụng định lí đường trung bình của hình thang: Độ dài đường trung bình của hình thang bằng nửa tổng hai đáy. Lời giải chi tiết: Cách giải: Độ dài đường trung bình của hình thang là \(\frac{3+7}{2}=5(cm)\) Chọn D Câu hỏi 11 : Một hình thang có đáy lớn là \(5cm\) , đáy nhỏ ngắn hơn đáy lớn là \(0,2cm\). Độ dài đường trung bình của hình thang là:
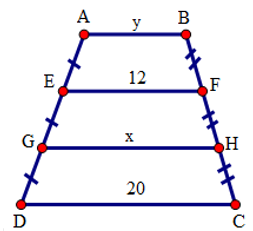
Đáp án: C Phương pháp giải: Phương pháp: Sử dụng định lí đường trung bình của hình thang: Độ dài đường trung bình của hình thang bằng nửa tổng hai đáy. Lời giải chi tiết: Cách giải: Độ dài đáy nhỏ của hình thang là: \(5-0,2=4,8(cm)\) . Độ dài đường trung bình của hình thang là \(\frac{5+4,8}{2}=4,9(cm)\) Chọn C Câu hỏi 12 : Tìm \(x,\text{ }y\) trên hình vẽ, trong đó \(AB//EF//GH//CD\).
Đáp án: C Phương pháp giải: Sử dụng định lí đường trung bình của hình thang Lời giải chi tiết: Vì \(EF//DC\) nên \(EFCD\) là hình thang. Lại có: \(GE=GD,FH=HC\) nên \(GH\) là đường trung bình của hình thang \(EFCD\) \(\Rightarrow GH=\frac{CD+EF}{2}=\frac{20+12}{2}=16(cm)=x\) Vì \(AB//GH\) nên \(ABHG\) là hình thang. Lại có: \(GE=EA,FH=BF\) nên \(EF\) là đường trung bình của hình thang \(ABHG\) \(\Rightarrow EF=\frac{AB+GH}{2}\Leftrightarrow 12=\frac{y+16}{2}\Leftrightarrow y=8(cm)\) . Vậy \(x=16cm,\,y=8cm\). Câu hỏi 13 : Một tam giác đều có độ dài cạnh bằng 12,5 cm. Độ dài đường trung bình của tam giác đó là:
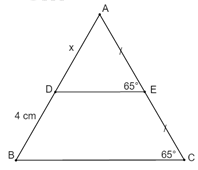
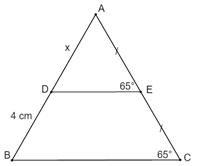
Đáp án: C Phương pháp giải: Dựa vào tính chất: đường trung bình của tam giác bằng một nửa cạnh đáy. Lời giải chi tiết: Cách giải: Độ dài đường trung bình của tam giác là: 12,5 : 2 = 6,25cm. Chọn C. Câu hỏi 14 : Cho hình vẽ sau: Khẳng định nào sau đây là đúng:
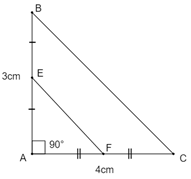
Đáp án: A Phương pháp giải: Áp dụng định nghĩa đường trung bình của tam giác: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. Lời giải chi tiết: Ta có: \(\angle AED = \angle ACB = {65^0}\) Mà hai góc này là hai góc ở vị trí đồng vị \( \Rightarrow DE//BC.\) Xét ∆ABC có: \(\left\{ \begin{array}{l}AE = EC\\DE//BD\end{array} \right.\) \( \Rightarrow \) \(DE\) là đường trung bình của \(\Delta ABC\) (định nghĩa). \( \Rightarrow D\) là trung điểm của \(AB\) (tính chất đường trung bình của tam giác). \( \Rightarrow AD = BD = 4cm\) Chọn A. Câu hỏi 15 : Cho tam giác ABC vuông tại A, \(AB = 3cm\),\(AC = 4cm\). Gọi E là trung điểm của AB, F là trung điểm của AC. Ta tính được độ dài EF là:
Đáp án: A Phương pháp giải: Áp dụng định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy Lời giải chi tiết: Áp dụng định lí Py-ta-go cho \(\Delta ABC\) vuông tại A ta có: \(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {3^2} + {4^2} = 25\\ \Rightarrow BC = 5cm\end{array}\) Mà \(\left\{ \begin{array}{l}AE = EB\,\,\,\left( {gt} \right)\\AF = FC\,\,\,\,\left( {gt} \right)\end{array} \right.\) \( \Rightarrow \)\(EF\) là đường trung bình của \(\Delta ABC\) (định nghĩa) \( \Rightarrow \)\({\rm{EF}} = \frac{1}{2}BC = \frac{1}{2} \times 5 = 2,5cm\) (tính chất đường trung bình của tam giác). Chọn A.
|