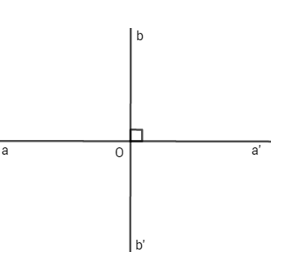
10 bài tập tổng hợp về Hai đường thẳng vuông gócLàm bàiCâu hỏi 1 : Cho hai đường thẳng aa’ và bb’ vuông góc với nhau tại O. Hãy chỉ ra câu sai trong các câu sau:
Đáp án: B Phương pháp giải: Quan sát hình vẽ, áp dụng định nghĩa hai đường thẳng vuông góc, tính các góc có số đo bằng 900. Lời giải chi tiết:
Hai đường thẳng aa’ và bb’ vuông góc với nhau tại O nên : +) \(\widehat{aOb}={{90}^{0}}\)=> A đúng. +) aa’ và bb’ vuông góc với nhau nên aa’ và bb’ cắt nhau => B sai. +) \(\widehat{a'Ob}=\widehat{a'Ob'}={{90}^{0}}\)=> aa’ là đường phân giác của góc bẹt bOb’ => C đúng. +) \(\widehat{b'Oa'}={{90}^{0}}\)=> D đúng. Chọn B. Câu hỏi 2 : Hãy chọn câu đúng trong các câu sau:
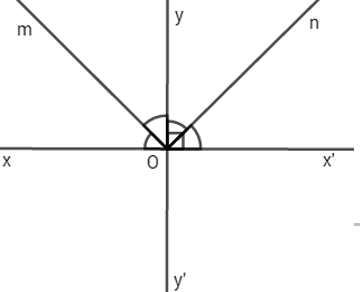
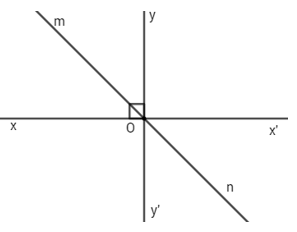
Đáp án: B Phương pháp giải: Áp dụng định nghĩa hai đường thẳng vuông góc. Lời giải chi tiết: Hai đường thẳng vuông góc thì cắt nhau. Chọn B. Câu hỏi 3 : Cho hai đường thẳng xx’ và yy’ vuông góc với nhau tại O. Vẽ tia Om là tia phân giác của góc xOy và On là tia phân giác của góc x’Oy. Tính số đo góc mOn.
Đáp án: A Phương pháp giải: Áp dụng định nghĩa hai đường thẳng vuông góc, tính chất tia phân giác của một góc. Từ đó cộng góc tính số đo góc mOn. Lời giải chi tiết: Vì xx’ và yy’ vuông góc với nhau tại O nên: \(\widehat{xOy}=\widehat{yOx'}={{90}^{0}}.\) Vì Om là tia phân giác của góc xOy nên: \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}{{.90}^{0}}={{45}^{0}}.\) Vì On là tia phân giác của góc yOx’ nên: \(\widehat{yOn}=\widehat{nOx'}=\frac{1}{2}\widehat{yOx'}=\frac{1}{2}{{.90}^{0}}={{45}^{0}}.\) Vì Oy nằm giữa hai tiaOm và On nên: \(\begin{align} & \widehat{mOy}+\widehat{yOn}=\widehat{mOn} \\ & {{45}^{0}}+{{45}^{0}}=\widehat{mOn} \\ & {{90}^{0}}=\widehat{mOn} \\ \end{align}\) Chọn A. Câu hỏi 4 : Cho hai đường thẳng xx’ và yy’ vuông góc với nhau tại O. Gọi Om là tia phân giác của góc xOy, On là tia đối của tia Om. Số đo góc x’On.
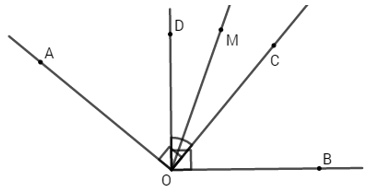
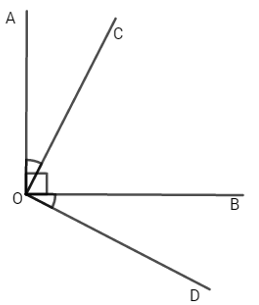
Đáp án: C Phương pháp giải: Áp dụng tính chất hai đường thẳng vuông góc, tính chất tia phân giác của một góc, tính chất hai góc đối đỉnh để tính số đo góc x’On. Lời giải chi tiết: Vì xx’ và yy’ vuông góc với nhau tại O nên: \(\widehat{xOy}=\widehat{yOx'}={{90}^{0}}.\) Vì Om là tia phân giác của góc xOy nên: \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}{{.90}^{0}}={{45}^{0}}.\) Vì On là tia đối của Om, Ox’ là tia đối của Ox nên \(\widehat{x'On}=\widehat{xOm}={{45}^{0}}.\) (tính chất hai góc đối đỉnh). Chọn C. Câu hỏi 5 : Cho góc AOB có số đo bằng 1400. Trong góc này vẽ hai tia OC và OD vuông góc với tia OA và OB. a) So sánh góc AOD và góc BOC. b) Tính số đo góc COD. c) Vẽ OM là tia phân giác của góc COD. Tia OM có phải là tia phân giác của góc AOB không? Vì sao?
Đáp án: A Phương pháp giải: a) Áp dụng tính chất tia nằm giữa hai tia còn lại, cộng góc, tính số đo góc AOD và BOC. Từ đó so sánh hai góc đó. b) Áp dụng tính chất tia nằm giữa hai tia còn lại, cộng góc, tính số đo góc COD. c) Áp dụng tính chất tia phân giác của một góc, chứng minh tia nằm giữa hai tia còn lại. Từ đó áp dụng công thức cộng góc, tính số đo góc AOM và BOM. Từ đó chứng minh OM là tia phân giác của góc AOB. Lời giải chi tiết: a) Vì tia OD nằm giữa hai tia OA và OB \(\begin{align} & \Rightarrow \widehat{AOD}+\widehat{DOB}=\widehat{AOB} \\ & \Rightarrow \widehat{AOD}+{{90}^{0}}={{140}^{0}} \\ & \Rightarrow \widehat{AOD}={{140}^{0}}-{{90}^{0}}={{50}^{0}}\,\,\,\,\,\,(1) \\ \end{align}\) Vì tia OC nằm giữa hai tia OA và OB \(\begin{align} & \Rightarrow \widehat{AOC}+\widehat{COB}=\widehat{AOB} \\& \Rightarrow {{90}^{0}}+\widehat{COB}={{140}^{0}} \\ & \Rightarrow \widehat{COB}={{140}^{0}}-{{90}^{0}}={{50}^{0}}\,\,\,\,\,\,(2) \\ \end{align}\) Từ (1) và (2) \(\Rightarrow \widehat{AOD}=\widehat{BOC}={{50}^{0}}\) b) Trên nửa mặt phẳng bờ chứa tia OA có : \(\widehat{AOD}<\widehat{AOC}\,\,\left( {{50}^{0}}<{{90}^{0}} \right)\) Suy ra tia OD nằm giữa hai tia OA và OC \(\begin{align} & \Rightarrow \widehat{AOD}+\widehat{COD}=\widehat{AOC} \\& \Rightarrow {{50}^{0}}+\widehat{COD}={{90}^{0}} \\ & \Rightarrow \widehat{COD}={{90}^{0}}-{{50}^{0}}={{40}^{0}}\,\,\,\,\, \\ \end{align}\) c) Vì OM là tia phân giác của góc COD nên \(\widehat{COM}=\widehat{DOM}=\frac{\widehat{COD}}{2}=\frac{40}{2}={{20}^{0}}\) OM là tia phân giác của góc COD nên OM nằm giữa hai tia OD và OC. Mà tia OD nằm giữa hai tia OA và OC. Suy ra OD nằm giữa hai tia OA và OM \(\begin{align} & \Rightarrow \widehat{AOD}+\widehat{DOM}=\widehat{AOM} \\ & \Rightarrow {{50}^{0}}+{{20}^{0}}=\widehat{AOM} \\ & \Rightarrow \widehat{AOM}={{70}^{0}}\,\,\,\,\, \\ \end{align}\) Chứng minh tương tự ta có : \(\widehat{BOM}={{70}^{0}}\,\) \(\Rightarrow \widehat{AOM}=\widehat{BOM}={{70}^{0}}\,\)và tia OM nằm giữa hai tia OA và OB. Vậy OM là tia phân giác của góc AOB. Chọn A Câu hỏi 6 : Cho góc AOB có số đo bằng 90o. Trong góc AOB vẽ tia OC. Trên nửa mặt phẳng bờ OB không chứa tia OC, vẽ tia OD sao cho \(\widehat{AOC}=\widehat{B\text{OD}}\). Tính số đo góc COD.
Đáp án: D Phương pháp giải: Sử dụng tính chất góc vuông, tính chất cộng góc để tính số đo góc COD. Lời giải chi tiết:
Vì OC nằm giữa tia OA và OB nên: \(\begin{align} & \widehat{AOC}+\widehat{COB}=\widehat{AOB} \\ & \widehat{AOC}+\widehat{COB}={{90}^{0}} \\ \end{align}\) Mà \(\widehat{AOC}=\widehat{BOD}\Rightarrow \widehat{BOD}+\widehat{COB}={{90}^{0}}.\) Lại có tia OB nằm giữa tia OC và OD nên \(\text{ }\widehat{BOD}+\widehat{COB}=\widehat{COD}.\)
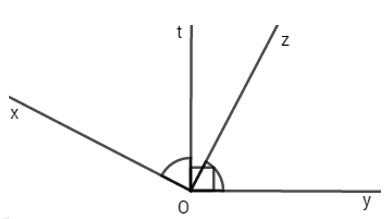
Vậy \(\widehat{COD}={{90}^{0}}.\) Chọn D. Câu hỏi 7 : Cho góc tOy có số đo bằng 90o. Vẽ tia Oz nằm trong góc tOy (tia Oz nằm giữa hai tia Ot và Oy). Bên ngoài góc tOy, vẽ tia Ox sao cho \(\widehat{xOt}=\widehat{\text{zOy}}\). Tính số đo của góc xOz.
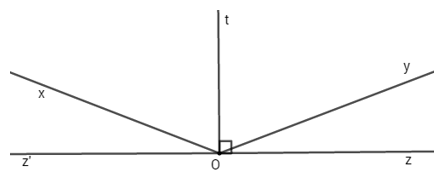
Đáp án: C Phương pháp giải: Sử dụng tính chất góc vuông, tính chất cộng góc để tính số đo \(\widehat{xOz}.\) Lời giải chi tiết: Vì Oz nằm giữa tia Ot và Oy nên: \(\begin{align} & \widehat{tOz}+\widehat{zOy}=\widehat{tOy} \\ & \widehat{tOz}+\widehat{zOy}={{90}^{0}} \\ \end{align}\) Mà \(\text{ }\widehat{xOt}=\widehat{zOy}\Rightarrow \widehat{tOz}+\widehat{xOt}={{90}^{0}}.\) Lại có tia Ot nằm giữa tia Ox và Oz nên \(\widehat{tOz}+\widehat{xOt}=\widehat{xOz}.\) Vậy \(\widehat{xOz}={{90}^{0}}.\) Chọn C. Câu hỏi 8 : Cho hai tia Ox và Oy vuông góc với nhau. Trong góc xOy vẽ hai tia Om và On sao cho \(\widehat{mOx}=\widehat{nOy}={{30}^{0}}\). Vẽ tia Oz sao cho tia Oy là tia phân giác của góc mOz. Chứng tỏ rằng: a) Tia Om là tia phân giác của góc nOx. b) On vuông góc với Oz. Phương pháp giải: a) Áp dụng tính chất tia nằm giữa hai tia còn lại. Từ đó áp dụng công thức cộng góc, tính số đo góc mOn. Từ đó chứng minh Om là tia phân giác của góc xOn. b) Áp dụng tính chất tia nằm giữa hai tia còn lại. Từ đó áp dụng công thức cộng góc, tính số đo góc nOz. Từ đó chứng minh On vuông góc với Oz. Lời giải chi tiết: a) Vì tia Om nằm giữa hai tia Ox và Oy \(\begin{align} & \Rightarrow \widehat{xOm}+\widehat{mOy}=\widehat{xOy} \\ & \Rightarrow {{30}^{0}}+\widehat{mOy}={{90}^{0}} \\ & \Rightarrow \widehat{mOy}={{90}^{0}}-{{30}^{0}}={{60}^{0}}\,\,\,\,\, \\ \end{align}\) Trên nửa mặt phẳng bờ chứa tia Oy có : \(\widehat{nOy}<\widehat{mOy}\,\,\left( {{30}^{0}}<{{60}^{0}} \right)\) Suy ra tia On nằm giữa hai tia Om và Oy \(\begin{align} & \Rightarrow \widehat{nOy}+\widehat{mOn}=\widehat{mOy} \\ & \Rightarrow {{30}^{0}}+\widehat{mOn}={{60}^{0}} \\ & \Rightarrow \widehat{mOn}={{60}^{0}}-{{30}^{0}}={{30}^{0}}\,\,\,\,\, \\ \end{align}\) \(\Rightarrow \widehat{xOm}=\widehat{mOn}={{30}^{0}}\) và tia Om nằm giữa hai tia Ox và On Vậy Om là tia phân giác của góc xOn. b) Vì Oy là tia phân giác của góc mOz nên \(\widehat{mOz}=2.\widehat{mOy}={{2.60}^{0}}={{120}^{0}}\) Trên nửa mặt phẳng bờ chứa tia Om có: \(\widehat{mOn}<\widehat{mOz}\,\,\left( {{30}^{0}}<{{120}^{0}} \right)\) Suy ra tia On nằm giữa hai tia Om và Oz \(\begin{align} & \Rightarrow \widehat{mOn}+\widehat{nOz}=\widehat{mOz} \\ & \Rightarrow {{30}^{0}}+\widehat{nOz}={{120}^{0}} \\ & \Rightarrow \widehat{nOz}={{120}^{0}}-{{30}^{0}}={{90}^{0}}\,\,\,\,\, \\ \end{align}\) Vậy On vuông góc với Oz. Câu hỏi 9 : Cho hai góc kề nhau xOy và yOz có tổng bằng 160o và \(\widehat{xOy}-\widehat{yOz}={{120}^{0}}\) a) Tính số đo góc xOy và góc yOz. b) Trong góc xOz, vẽ tia Ot vuông góc với tia Oz. Tia Ot có phải là tia phân giác của góc xOy không? Vì sao? c) Vẽ tia Oz’ là tia đối của tia Oz. So sánh góc xOz và yOz’.
Đáp án: C Phương pháp giải: a) Dựa vào giả thiết của bài toán, rút một góc theo góc còn lại. Thay vào tính số đo 2 góc đó. b) Áp dụng tính chất tia nằm giữa hai tia còn lại. Từ đó áp dụng công thức cộng góc, tính số đo góc xOt và góc tOy. Từ đó chứng minh Ot là tia phân giác của góc xOy. c) Áp dụng tính chất tia nằm giữa hai tia còn lại, cộng góc để tính số đo góc yOz’. Từ đó so sánh số đo góc xOz và yOz’. Lời giải chi tiết: a) Theo đề bài ta có: \(\widehat{xOy}-\widehat{yOz}={{120}^{0}}\Rightarrow \widehat{xOy}={{120}^{0}}+\widehat{yOz}\) Mà \(\widehat{xOy}+\widehat{yOz}={{160}^{0}}\) \(\begin{align}& \Rightarrow {{120}^{0}}+\widehat{yOz}+\widehat{yOz}={{160}^{0}} \\ & \Rightarrow {{120}^{0}}+2.\widehat{yOz}={{160}^{0}} \\ & \Rightarrow 2.\widehat{yOz}={{160}^{0}}-{{120}^{0}}={{40}^{0}} \\ & \Rightarrow \widehat{yOz}={{20}^{0}} \\ & \Rightarrow \widehat{xOy}={{120}^{0}}+{{20}^{0}}={{140}^{0}} \\ \end{align}\) b) Vì tia Ot nằm giữa hai tia Ox và Oz \(\begin{align} & \Rightarrow \widehat{xOt}+\widehat{tOz}=\widehat{xOz} \\ & \Rightarrow \widehat{xOt}+{{90}^{0}}={{160}^{0}} \\ & \Rightarrow \widehat{xOt}={{160}^{0}}-{{90}^{0}}={{70}^{0}}\,\,(1) \\ \end{align}\) Trên nửa mặt phẳng bờ chứa tia Oz có: \(\widehat{yOz}<\widehat{tOz}\,\,\left( {{20}^{0}}<{{90}^{0}} \right)\) Suy ra tia Oy nằm giữa tia Ot và Oz \(\begin{align}& \Rightarrow \widehat{tOy}+\widehat{yOz}=\widehat{tOz} \\ & \Rightarrow \widehat{tOy}+{{20}^{0}}={{90}^{0}} \\ & \Rightarrow \widehat{tOy}={{90}^{0}}-{{20}^{0}}={{70}^{0}}\,\,\,(2) \\ \end{align}\) Từ (1) và (2) \(\Rightarrow \widehat{xOt}=\widehat{tOy}={{70}^{0}}\) và tia Ot nằm giữa hai tia Ox và Oy. Vậy Ot là tia phân giác của góc xOy. c) Vì Oz’ là tia đối của tia Oz nên \(\widehat{zOz'}={{180}^{0}}\). Trên nửa mặt phẳng bờ chứa tia Oz có: \(\widehat{yOz}<\widehat{zOz'}\,\,\left( {{20}^{0}}<{{180}^{0}} \right)\) Suy ra tia Oy nằm giữa hai tia Oz và Oz’ \(\begin{align} & \Rightarrow \widehat{yOz}+\widehat{yOz'}=\widehat{zOz'} \\ & \Rightarrow {{20}^{0}}+\widehat{yOz'}={{180}^{0}} \\ & \Rightarrow \widehat{yOz'}={{180}^{0}}-{{20}^{0}}={{160}^{0}} \\ \end{align}\) \(\Rightarrow \widehat{xOz}=\widehat{yOz'}={{160}^{0}}\) Chọn C Câu hỏi 10 : Ở ngoài góc tù xOy, vẽ các tia Oz, Ot sao cho Oz vuông góc với Ox, Ot vuông góc với Oy. Gọi Om, On là tia phân giác của góc xOy, zOt. Chứng minh Om, On là hai tia đối nhau. Phương pháp giải: Áp dụng công thức cộng góc, tính chất tia phân giác của một góc, tính số đo góc mOn. Áp dụng tính chất hai tia đối để chứng minh Om và On là hai tia đối nhau. Lời giải chi tiết: Vì Oz, Ot nằm ngoài góc xOy nên \(\widehat{xOy}+\widehat{yOt}+\widehat{tOz}+\widehat{\text{zOx}}={{360}^{0}}\). Mà \(\widehat{yOt}+\widehat{\text{zOx}}={{90}^{0}}+{{90}^{0}}={{180}^{0}}.\) \(\Rightarrow \widehat{xOy}+\widehat{\text{tOz}}={{360}^{0}}-{{180}^{0}}={{180}^{0}}.\) Vì Om là tia phân giác góc xOy \(\Rightarrow \widehat{mOy}=\frac{1}{2}.\widehat{xOy}\) Vì On là tia phân giác góc tOz \(\Rightarrow \widehat{tOn}=\frac{1}{2}.\widehat{tOz}\) \(\Rightarrow \widehat{mOy}+\widehat{\text{tOn}}=\frac{1}{2}(\widehat{xOy}+\widehat{\text{tOz}})=\frac{1}{2}{{.180}^{0}}={{90}^{0}}.\) Ta có: \(\widehat{mOn}=\widehat{mOy}+\widehat{tOn}+\widehat{\text{yOt}}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\) Vậy hai tia Om và On là hai tia đối nhau.
|