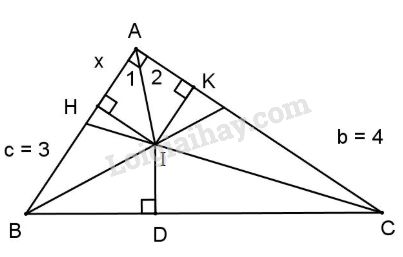
Đề kiểm tra 15 phút - Đề số 8 - Bài 5, 6 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC vuông tại A, biết AB = 3cm; AC = 4cm, phân giác của hai góc B và C cắt nhau tại I. Vẽ IH, IK lần lượt vuông góc với AB và AC. Tính khoảng cách từ I đến các cạnh của tam giác.

Lời giải chi tiết

Cách 1: 

Ta có $BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{3^2} + {4^2}}  = 5$ (cm) (định lý Pytago).

AI là phân giác của $\widehat A$ $\Rightarrow {\widehat A_1} = {\widehat A_2} = \dfrac{{\widehat A}}{2} = {45^0}.$

Do đó $\Delta AHI$ và $\Delta AKI$ là các tam giác vuông cân $\Rightarrow AH = IH$ và $AK = IK.$

Mặt khác vì I thuộc phân giác góc A nên $IH = IK \Rightarrow IH = IK = AK = AH.$

Kẻ $I{\rm{D}} \bot BC$, ta cũng có $I{\rm{D}} = IH$ (do hai tam giác BHI và BDI bằng nhau (cạnh huyền-góc nhọn))

Gọi ba cạnh BC, AC, AB của tam giác ABC lần lượt  là a, b, c. Đặt $AH = x$ thì $AH=AK=IH=IK=ID=x$

Ta có $BH+HA=AB$ hay $BH=AB-AH=c-x$

Suy ra $BH = B{\rm{D}} = c - x$;

Tương tự $CK = C{\rm{D}} = b - x,$ mà $a = B{\rm{D}} + C{\rm{D}}$ nên $a = c - x + b - x$

$\Rightarrow x = \dfrac{{b + c - a} }{ 2} = \dfrac{{4 + 3 - 5} }{2} = 1$ (cm).

Vậy $HI = I{\rm{D}} = IK = x = 1$ (cm).

Cách 2:

$IH = IK = I{\rm{D}} = x;$$\;{S_{\Delta ABC}} = \dfrac{{AB.AC} }{ 2} = 6.$ 

$\eqalign{   {S_{\Delta ABC}} &= {S_{\Delta AIC}} + {S_{\Delta AIB}} + {S_{\Delta BIC}} \cr&= {1 \over 2}IK.AC + {1 \over 2}IA.AB  \cr  & {\rm{        }} = {x \over 2}(ac + ab + bc) = 6x \cr}$      

$\Rightarrow 6x=6 \Rightarrow x = 1.$

HocTot.Nam.Name.Vn