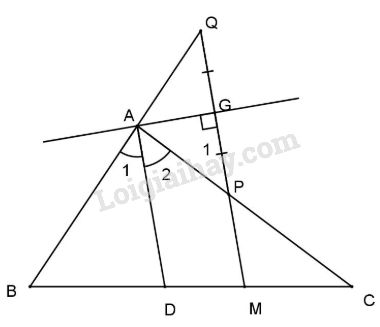
Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 3 – Hình học 7 Đề bài Cho ta giác ABC, phân giác AD. Lấy M bất kỳ thuộc đoạn DC, từ M kẻ đường thẳng song song với AD cắt AC tại P và cắt tia BA tại Q. Chứng minh rằng: Trung trực của đoạn PQ đi qua đỉnh A. Phương pháp giải - Xem chi tiết Sử dụng: -Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì: +Hai góc đồng vị bằng nhau +Hai góc so le trong bằng nhau -Tính chất tia phân giác -Tính chất tam giác cân
Lời giải chi tiết
Ta có MQ // AD (gt) \( \Rightarrow \widehat Q = {\widehat A_1}\) (đồng vị) và \({\widehat P_1} = {\widehat A_2}\) (so le trong), Mà AD là phân giác góc \(\widehat {BA{\rm{D}}}\) (gt) \( \Rightarrow {\widehat A_1} = {\widehat A_2} \Rightarrow \widehat Q = {\widehat P_1}\) hay \(\Delta AQP\) cân tại A. Do đó đường trung trực của đáy PQ phải đi qua đỉnh A. HocTot.Nam.Name.Vn
|