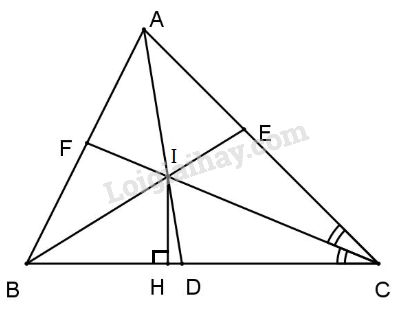
Đề kiểm tra 15 phút - Đề số 7 - Bài 5, 6 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC; các phân giác AD, BE, CF gặp nhau tại I.

a) Tính $\widehat {IAC} + \widehat {IBC} + \widehat {IC{\rm{A}}}.$

b) Kẻ IH vuông góc với BC (H thuộc BC). Chứng minh $\widehat {BIH} = \widehat {CI{\rm{D}}}.$

Lời giải chi tiết

a) Ta có $\widehat A + \widehat B + \widehat C = {180^0}$

$\Rightarrow \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B}}{ 2} + \dfrac{{\widehat C}}{ 2} = {90^0}$
hay $\widehat {IAC} + \widehat {IBC} + \widehat {ICA} = {90^0}.$

b) Từ $\widehat A + \widehat B + \widehat C = {180^0}$

$\eqalign{  &  \Rightarrow \widehat A + \widehat C = {180^0} - \widehat B  \cr  &  \Rightarrow {{\widehat A} \over 2} + {{\widehat C} \over 2} = {{{{180}^0} - \widehat B} \over 2} \cr}$

hay $\widehat {IAC} + \widehat {ICA} = {90^0} - \dfrac{{\widehat B} }{ 2},$

Mà $\widehat {CI{\rm{D}}}$ là góc ngoài của $\Delta AIC$ nên $\widehat {CI{\rm{D}}} = \widehat {IAC} + \widehat {IC{\rm{A}}} = {90^0} -\dfrac {{\widehat B} }{ 2}$  (1).

Mặt khác $\Delta IHB$ vuông tại H $\Rightarrow \widehat {BIH} + \widehat {IC{\rm{A}}} = {90^0}$

$\Rightarrow \widehat {BIH} = {90^0} - \widehat {IBC}$ hay $\widehat {BIH} = {90^0} - \dfrac{{\widehat B} }{ 2}$   (2)

Từ (1) và (2) $\Rightarrow \widehat {BIH} = \widehat {CI{\rm{D}}} = {90^0} - \dfrac{{\widehat B} }{2}.$

HocTot.Nam.Name.Vn