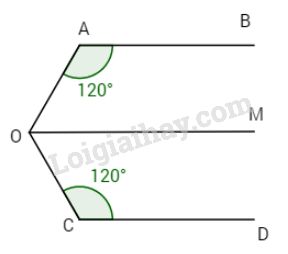
Đề kiểm tra 15 phút - Đề số 11 - Bài 5, 6 - Chương 1 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 11 - Bài 5, 6 - Chương 1 - Hình học 7 Đề bài Bài 1: Cho hình vẽ.
Biết AB // CD // OM và \(\widehat A = \widehat C = {120^o}\). Hỏi OM có là phân giác của \(\widehat {AOC}\) hay không? Bài 2: Cho hình vẽ.
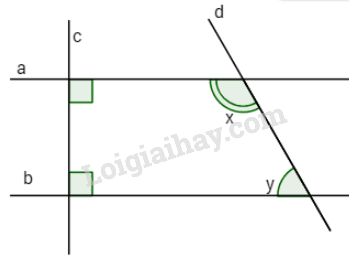
Biết \(2\widehat x = 3\widehat y\). Tính \(\widehat x;\,\widehat y\). Phương pháp giải - Xem chi tiết Sử dụng: Nếu một đường thẳng cắt hai đường thẳng song song thì: a) Hai góc so le trong bằng nhau. b) Hai góc đồng vị bằng nhau. c) Hai góc trong cùng phía bù nhau. Lời giải chi tiết Bài 1: AB // OM\( \Rightarrow \widehat {AOM} + \widehat {BAO} = {180^o}\) (cặp góc trong cùng phía bù nhau) \( \Rightarrow \widehat {AOM} = {180^o} - \widehat {BAO} \)\(\,= {180^o} - {120^o} = {60^o}\). Tương tự CD // OM \( \Rightarrow \widehat {MOC} + \widehat {OCD} = {180^o} \)\(\,\Rightarrow \widehat {MOC} = {180^o} - {120^o} = {60^o}\). Ta có \(\widehat {AOM} = \widehat {MOC} = {60^o}\). Do đó OM là tia phân giác của \(\widehat {AOC}\). Bài 2: Ta có : \(\left\{ \matrix{a \bot c \hfill \cr b \bot c \hfill \cr} \right. \Rightarrow a//b \Rightarrow \widehat x + \widehat y = {180^o}\) (cặp góc trong cùng phía bù nhau), Lại có \(2\widehat x = 3\widehat y\)\(\; \Rightarrow \dfrac{{\widehat x}}{3} =\dfrac {{\widehat y} }{ 2} = \dfrac{{\widehat x + \widehat y}}{ {3 + 2}} = \dfrac{{{{180}^o}} }{ 5} = {36^o}.\) Do đó \(\widehat x =36^0.3= {108^o}\) và \(\widehat y =36^0.2= {72^o}\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
