Nội dung từ Loigiaihay.Com
Đề bài
Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$ và các cạnh bên đều bằng $a$. Gọi $M$ và $N$ lần lượt là trung điểm của $AD$ và $SD$. Số đo của góc $\left( {MN,SC} \right)$ bằng:
-
A.
$45^\circ $
-
B.
$30^\circ $
-
C.
$90^\circ $
-
D.
$60^\circ $
Phương pháp giải
- Chứng minh \(SA \bot SC\) bằng cách sử dụng định lý Pi-ta-go.
- Sử dụng tính chất \(\left\{ \begin{array}{l}a \bot b\\b//c\end{array} \right. \Rightarrow a \bot c\)
Lời giải của GV HocTot.Nam.Name.Vn
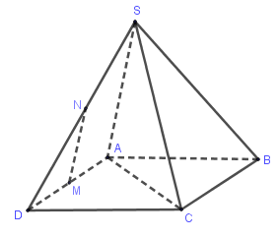
Ta có: $AC = a\sqrt 2 $
$ \Rightarrow A{C^2} = 2{a^2} = S{A^2} + S{C^2}$
$ \Rightarrow \Delta SAC$ vuông tại $S$.
Khi đó: $\overrightarrow {NM} .\overrightarrow {SC} = \dfrac{1}{2}\overrightarrow {SA} .\overrightarrow {SC} = 0$ $ \Leftrightarrow \left( {\overrightarrow {NM} ,\overrightarrow {SC} } \right) = 90^\circ $
$ \Rightarrow \left( {MN,SC} \right) = 90^\circ $
Đáp án : C
Các bài tập cùng chuyên đề