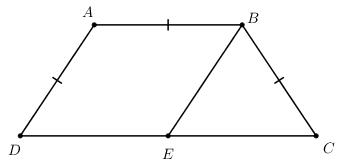
Bài tập 8 trang 104 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho hình thang ABCD (AB và CD là hai đáy và AB < CD), AD = BC = AB, $\widehat {BDC} = {30^o}$ .

Tính các góc của hình thang.

Lời giải chi tiết

Ta có $AD = AB\,\,\left( {gt} \right) \Rightarrow \Delta ABD$ cân tại A $\Rightarrow \widehat {ADB} = \widehat {ABD}$

Mà $\widehat {ABD} = \widehat {BDC}$ (so le trong và AB // CD) và $\widehat {BDC} = {30^0}\,\,\left( {gt} \right)$ nên $\widehat {ADB} = \widehat {ABD} = {30^0}$

Ta có $\widehat {ADC} = \widehat {ADB} + \widehat {BDC} = {30^0} + {30^0} = {60^0}$

$\widehat {BAD} + \widehat {ADC} = {180^0}$ (hai góc trong cùng phía và AB // CD)

Do đó $\widehat {BAD} + {60^0} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {60^0} = {120^0}$

Trên cạnh CD lấy điểm E sao cho $DE = AB$

Hình thang ABED $\left( {AB//DE} \right)$ có $AB = DE$

$\Rightarrow BE//AD$ và $BE = AD$

$BE = BC\,\,\left( { = AD} \right) \Rightarrow \Delta BEC$ cân tại B $\Rightarrow \widehat {BEC} = \widehat {BCD}$

Mặt khác $\widehat {BEC} = \widehat {ADC}$ (đồng vị và AD // BE)

Do đó $\widehat {BCD} = \widehat {ADC} = {60^0}$

Mặt khác $\widehat {ABC} + \widehat {BCD} = {180^0}$ (hai góc trong cùng phía và AB // CD)

Do đó $\widehat {ABC} = {180^0} - \widehat {BCD} = {180^0} - {60^0} = {120^0}$

HocTot.Nam.Name.Vn