Nội dung từ Loigiaihay.Com
Cho a,b,c>0 thỏa mãn: 6a+2b+3c=11. Tìm giá trị nhỏ nhất của biểu thức M=2b+3c+161+6a+6a+3c+161+2b+6a+2b+161+3c.
-
A.
8
-
B.
9
-
C.
15
-
D.
11
Biến đổi để sử dụng bất đẳng thức ab+ba≥2 với a,b>0.
Dấu “=” xảy ra khi a=b.
Đặt x=1+6a;y=1+2b;z=1+3c(x,y,z>0)
⇒x+y+z=1+6a+1+2b+1+3c=3+(6a+2b+3c)=3+11=14
Ta có: 2b+3c+16=y−1+z−1+16=y+z+14
6a+3c+16=x+z+14
6a+2b+16=x+y+14
Từ đó: M=z+y+14x+x+z+14y+x+y+14z
=zx+yx+14x+xy+zy+14y+xz+yz+14z
=(xy+yx)+(yz+zx)+(zx+xz)+14(1x+1y+1z)
=(xy+yx)+(yz+zx)+(zx+xz)+(x+y+z)(1x+1y+1z)
=2(xy+yx)+2(yz+zx)+2(zx+xz)+3
Mặt khác: xy+yx≥2 dấu “ = ” xảy ra khi và chỉ khi x=y
xz+zx≥2. Dấu “ = ” xảy ra khi và chỉ khi x=z
zy+yz≥2. Dấu “ = ” xảy ra khi và chỉ khi z=y
Khi đó: M≥2.2+2.2+2.2+3⇒M≥15. Dấu “ = ” xảy ra khi và chỉ khi x=y=z=1
Suy ra: a=1118;b=116;c=119.
Vậy Mmin=15 khi a=1118;b=116;c=119.
Đáp án : C

Các bài tập cùng chuyên đề
Khi x≥3, kết quả rút gọn của biểu thức 2x+|x−3|−1 là:
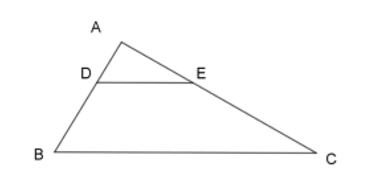
Cho hình vẽ, biết DE//BC. Khẳng định nào sau đây là đúng?
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là:
Cho ΔMNP∽ có tỉ số chu vi: \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}. Chọn câu đúng.
Giá trị x = 2 là nghiệm của bất phương trình nào dưới đây?
Rút gọn biểu thức {\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}, ta được kết quả là:
Phân tích đa thức 5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3} thành nhân tử ta được:
Phương trình 7x + 4\; = 3x-{\rm{ }}1 có tập nghiệm là:
Phương trình {x^3} - 9x = 0 có bao nhiêu nghiệm?
Phương trình \left| {x - 4} \right| + 3x = 5 có tổng các nghiệm là:
Giải phương trình \dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}} ta được nghiệm là:
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.












