Cho hàm số $f\left( x \right) = {2^{{x^2} + 1}}$. Tính $T = {2^{ - {x^2} - 1}}.f'\left( x \right) - 2x\ln 2 + 2$.

Hàm số $y = {a^x}\left( {0 < a \ne 1} \right)$ đồng biến khi nào?

Chọn khẳng định đúng:

Chọn mệnh đề đúng:

Chọn mệnh đề đúng:

Chọn mệnh đề đúng:

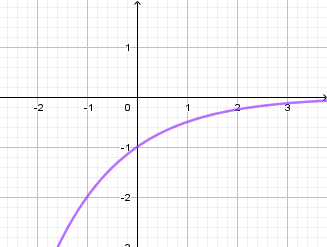
Đồ thị sau là đồ thị hàm số nào?

Đồ thị hàm số dưới đây là của hàm số nào?

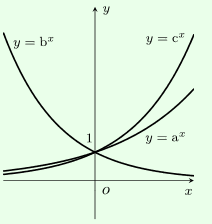
Cho các đồ thị hàm số $y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)$, chọn khẳng định đúng:

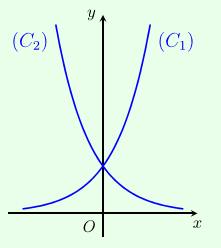
Cho hai hàm số $y = {a^x},y = {b^x}$ với $1 \ne a,b > 0$ lần lượt có đồ thị là $\left( {{C_1}} \right),\left( {{C_2}} \right)$ như hình bên. Mệnh đề nào đúng?

Hàm số $y = {2^{\ln x + {x^2}}}$ có đạo hàm là

Cho hàm số $y = {3^x} + \ln 3$. Chọn mệnh đề đúng:

Cho giới hạn $I = \mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{3x}} - {e^{2x}}}}{x}$, chọn mệnh đề đúng:

Cho $a$ là số thực dương khác $1$. Xét hai số thực $x_1, x_2$. Phát biểu nào sau đây là đúng?

Cho hàm số $f\left( x \right) = {2^x}{.7^{{x^2}}}$. Khẳng định nào sau đây là khẳng định sai?

Cho các số thực dương $a, b$ khác $1$. Biết rằng đường thẳng $y=2$ cắt đồ thị các hàm số $y = {a^x};y = {b^x}$ và trục tung lần lượt tại $A, B, C$ sao cho $C$ nằm giữa $A$ và $B$, và $AC= 2BC$. Khẳng định nào dưới đây đúng?

Gọi $m$ là GTLN của hàm số $f\left( x \right) = {e^{{x^3} - 3x + 3}}$ trên đoạn $\left[ {0;2} \right]$. Chọn kết luận đúng:

Gọi $m,M$ lần lượt là GTNN, GTLN của hàm số $y = {e^{2 - 3x}}$ trên đoạn $\left[ {0;2} \right]$. Mệnh đề nào sau đây đúng?

Cho hai số thực dương $x, y$ thỏa mãn ${2^x} + {2^y} = 4$. Tìm giá trị lớn nhất ${P_{\max }}$ của biểu thức$P = (2{x^2} + y)(2{y^2} + x) + 9xy$.

Cho hàm số $f(x) = {(3 - \sqrt 2 )^{{x^3}}} - {\left( {3 - \sqrt 2 } \right)^{ - {x^2}}}$ . Xét các khẳng định sau:

Khẳng định 1: $f(x) > 0 \Leftrightarrow {x^3} + {x^2} > 0$

Khẳng định 2: $f(x) > 0 \Leftrightarrow x >  - 1$.

Khẳng định 3: $f(x) < 3 - \sqrt 2  \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {\left( {\dfrac{{3 + \sqrt 2 }}{7}} \right)^{{x^2} + 1}}$

Khẳng định 4:$f(x) < 3 + \sqrt 2  \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} + 1}} < {(3 - \sqrt 2 )^{1 - {x^2}}} + 7$

Trong các khẳng định trên, có bao nhiêu khẳng định đúng?

Cho hàm số $f\left( x \right) = \dfrac{1}{{3 + {2^x}}} + \dfrac{1}{{3 + {2^{ - x}}}}$. Trong các khẳng định, có bao nhiêu khẳng định đúng?

1) $f'\left( x \right) \ne 0,\forall x \in R$

2) $f\left( 1 \right) + f\left( 2 \right) + ... + f\left( {2017} \right) = 2017$

3) $f\left( {{x^2}} \right) = \dfrac{1}{{3 + {4^x}}} + \dfrac{1}{{3 + {4^{ - x}}}}$