Nội dung từ Loigiaihay.Com
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(BC = R.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B,C\) cắt nhau tại \(A.\) Gọi \(M\) là giao điểm của \(AO\) và \(BC.\) Khi đó tam giác \(AMB\) là:
-
A.
Tam giác vuông có một góc \({30^0}\)
-
B.
Tam giác vuông có một góc \({60^0}\)
-
C.
Tam giác có cạnh góc vuông bằng nửa cạnh huyền
-
D.
Các đáp án trên đều đúng
+ Sử dụng góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn
+ Tổng ba góc trong tam giác bằng $180^0$
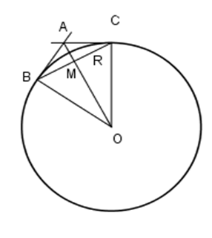
Xét đường tròn $(O)$ có dây \(BC = R = OC = OB\) nên \(\Delta BOC\) là tam giác đều. Do đó
\(\widehat {BOC} = {60^0} \Rightarrow \) sđ \(\overparen{BC} = {60^0}\)
Lại có \(\widehat {ABC}\) là góc tạo bởi hai tiếp tuyến \(BA\) và dây cung \(BC\) của \(\left( O \right).\)
Do góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn nên \(\widehat {ABC} = \dfrac{1}{2}\) sđ \(\overparen{BC} = {30^0}\).
Lại có $AB=AC$ (tính chất hai tiếp tuyến cắt nhau) và $OB=OC=R$ nên $AO$ là đường trung trực của $BC$
Hay $AO \bot BC$ tại $M$, suy ra \(\widehat {AMB} = {90^0} \Rightarrow \widehat {BAM} = {60^0}.\)
Như vậy tam giác $AMB$ vuông tại $M$ và có \(\widehat {ABM} = {30^0};\, \widehat {BAM} = {60^0}\)
Nên đáp án A, B đều đúng.
Ta lại có \(\sin \widehat {ABM} = \dfrac{{AM}}{{AB}} \Rightarrow \dfrac{{AM}}{{AB}} = \sin \,{30^0} = \dfrac{1}{2}.\)
Hay cạnh góc vuông \(AM\) bằng nửa cạnh huyền \(AB.\) Vì vậy đáp án C cũng đúng.
Đáp án : D

Các bài tập cùng chuyên đề
Số đo cung lớn \(BnC\) trong hình bên là:

Cho hình vẽ ở bên. Khi đó mệnh đề đúng là:
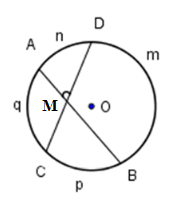
Cho hình vẽ (hai đường tròn có tâm là \(B,C \) và điểm \(B\) nằm trên đường tròn tâm \(C\)). Biết $\widehat {MAN} = {20^0}.$
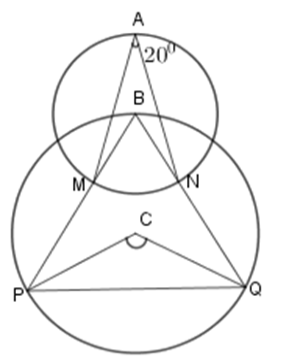
Khi đó \(\widehat {PCQ} = ?\)
Cho hình vẽ bên. Mệnh đề nào sau đây là sai.
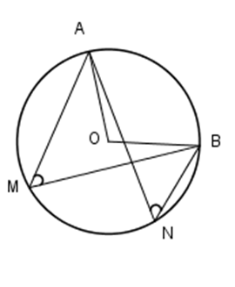
Cho đường tròn \(\left( O \right)\) Trên \(\left( O \right)\) lấy ba điểm \(A,B,D\) sao cho \(\widehat {AOB} = {120^0},\,\,AD = BD.\)
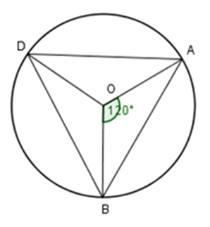
Khi đó \(\Delta ABD\) là:
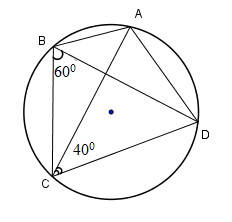
Cho bốn điểm A, B, C, D thuộc đường tròn \(\left( O \right).\) Biết \(\widehat {BOD} = {130^0}\) thì số đo \(\widehat {BAD}\) là:
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) cắt nhau tại \(A\) và \(B.\) Vẽ cát tuyến \(CAD\) vuông góc với \(AB\left( {C \in \left( O \right),D \in \left( {O'} \right)} \right)\) . Tia \(CB\) cắt \(\left( {O'} \right)\) tại \(E,\) tia \(DB\) cắt \(\left( O \right)\) tại \(F.\) Khi đó
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
Cho hình vẽ dưới đây.
Khi đó mệnh đề đúng là:
Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai cát tuyến \(ABC\) và \(ADE\) với đường tròn đó (\(B\) nằm giữa \(A\) và \(C,\)\(D\) nằm giữa \(A\) và \(E\)). Kẻ dây \(BF//DE.\) Khi đó kết luận đúng là:
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
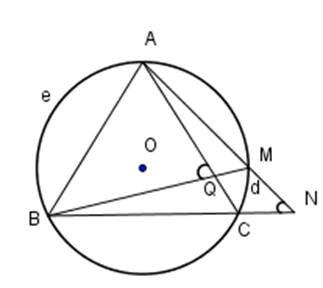
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O.\) Gọi $P,\,Q,R$ lần lượt là giao điểm của các tia phân giác trong góc \(A,\,B,\,C\) với đường tròn. Giả sử rằng \(S = AP \cap RQ.\) Khi đó:
Cho tam giác nhọn \(ABC\,\,\left( {AB > BC} \right)\) nội tiếp đường tròn \(\left( O \right).\) \(D\) là điểm chính giữa cung \(AC.\) Giả sử \(\{E\} = AB \cap CD,\,\,\{F\} = AD \cap BC.\) Khi đó :
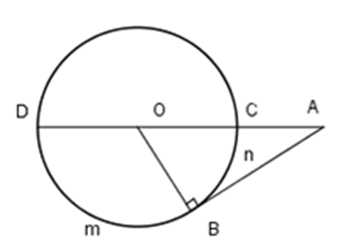
Cho hình vẽ, biết số đo cung \(BmD\) là \({120^0}.\) Khi đó
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\)
.PNG)
Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
Cho điểm \(C\) thuộc nửa đường tròn \(\left( O \right)\) đường kính \(AB.\) Từ điểm \(D\) thuộc đọan \(AO\) kẻ đường thẳng vuông góc với \(AO\) cắt \(AC\) và \(BC\) lần lượt lại \(E\) và \(F.\) Tiếp tuyến tại \(C\) với nửa đường tròn cắt $EF$ tại \(M\) và cắt \(AB\) tại \(N.\) Khi đó
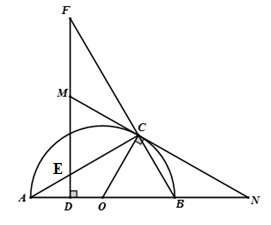
Cho đường tròn tâm \(O,\) đường kính \(AB.\) Lấy điểm \(P\) khác \(A\) và \(B\) trên đường tròn sao cho \(\widehat {BAP} = {30^0}.\) Gọi \(T\) là giao điểm của \(AP\) với tiếp tuyến tại \(B\) của đường tròn. Khi đó ta có \(\widehat {PBT} = ?\)
Cho hình vẽ ở bên. Biết \( \widehat {BAx}=20^0\).
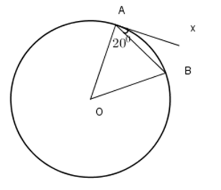
Hãy tính số đo của cung bị chắn \(AB.\)
Cho hình vẽ. Khi đó đáp án đúng là
Tia phân giác góc \(\widehat {BAD}\) của hình bình hành \(ABCD\) cắt các đường thẳng \(BC\) và \(DC\) lần lượt tại hai điểm \(M\) và \(N.\) Dựng ra phía ngoài hình bình hành \(ABCD\) tam giác \(MCO\) cân tại $O$ với \(\widehat {MOC} = \widehat {BAD}\). Khi đó:












