Cho hàm số y = f(x) liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình dưới.

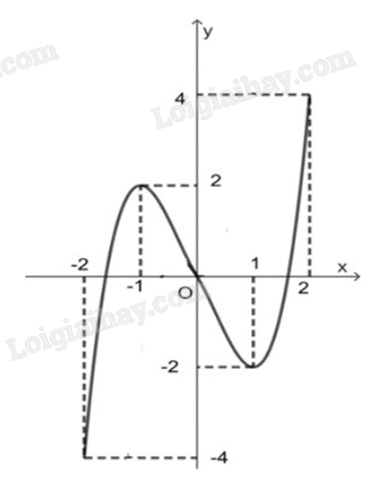
Hàm số y = f(x) đạt cực tiểu tại điểm

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc $(a;b)$ thì

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ dương sang âm qua điểm ${x_0}$ thì:

Giải thích vì sao nếu f’(x) không đổi dấu qua ${x_0}$ thì ${x_0}$ không phải là điểm cực trị của hàm số f(x)?

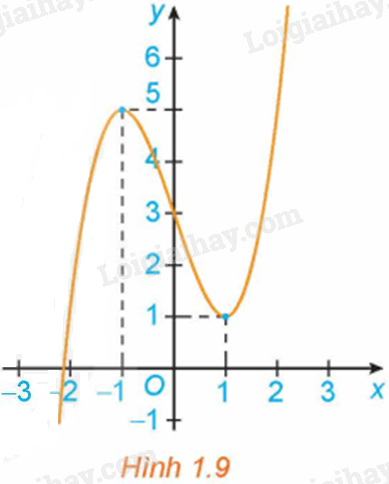
Hình 1.9 là đồ thị của hàm số $y = f\left( x \right)$. Hãy tìm các cực trị của hàm số.

Cho hàm số $y = f\left( x \right) = \left| x \right|$.
a) Tính các giới hạn $\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}$ và $\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}$. Từ đó suy ra hàm số không có đạo hàm tại $x = 0$.
b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại $x = 0$. (Xem Hình 1.4)

Quan sát bảng biến thiên dưới đây và cho biết:

a) ${x_o}$ có là điểm cực đại của hàm số $f\left( x \right)$ hay không.

b) ${x_1}$ có là điểm cực tiểu của hàm số $h\left( x \right)$ hay không.

Dựa vào đồ thị hàm số $y = f\left( x \right) =  - {x^3} - 3{x^2} + 3$ ở Hình 3, hãy so sánh:

a) $f\left( { - 2} \right)$ với mỗi giá trị $f\left( x \right)$, ở đó $x \in \left( { - 3; - 1} \right)$ và $x \ne  - 2$.

b) $f\left( 0 \right)$với mỗi giá trị $f\left( x \right)$, ở đó $x \in \left( { - 1;1} \right)$ và $x \ne 0$.

Cho hàm số $y = f\left( x \right)$có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng:
a) $2$.
b) $3$.
c) $- 4$.
d) $0$.

Đồ thị của hàm số $y = \left\{ \begin{array}{l}{x^2}{\rm{       }}khi{\rm{ }}x \le 1{\rm{ }}\\2 - x{\rm{   }}khi{\rm{ }}x > 1\end{array} \right.$ được cho ở Hình 9.

a) Tìm điểm cực đại và điểm cực tiểu của hàm số.

b) Tại x = 1, hàm số có đạo hàm không?

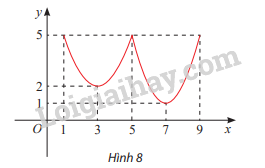
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại và điểm cực tiểu.

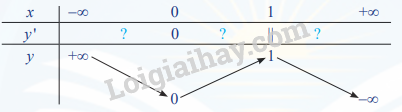
Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8

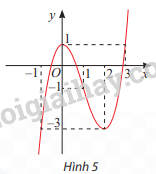
Quan sát đồ thị của hàm số $y = f\left( x \right) = {x^3}--3{x^2} + 1{\rm{ }}$ trong Hình 5.

a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi $x \ne 0$.

b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi $x \ne 2$.

c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi $x \ne 1$ hoặc f(x) < f(1) với mọi $x \ne 1$?

Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số đạt cực đại tại

A. x = 0.      B. x = 3.      C. x = 4.      D. x = 5.

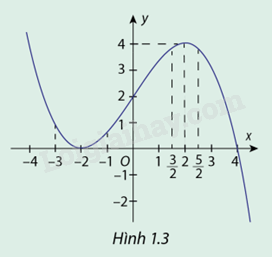
Hàm số $y = f(x) =  - \frac{1}{8}{x^3} + \frac{3}{2}x + 2$ có đồ thị cho ở hình 1.3

a) Giải phương  trình $f'(x) = 0$

b) Dựa vào đồ thị, só sánh $f( - 2)$ với các giá trị khi $x \in ( - 3; - 1)$

c) Dựa vào đồ thị, só sánh $f(2)$ với các giá trị khi  $x \in \left( {\frac{3}{2};\frac{5}{2}} \right)$

Cho hàm số f(x) có đạo hàm $f'(x) = x{(x + 1)^2}{(x - 2)^3}$, $\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số là

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là:

A. 0.

B. 1.

C. 2.

D. 3.

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

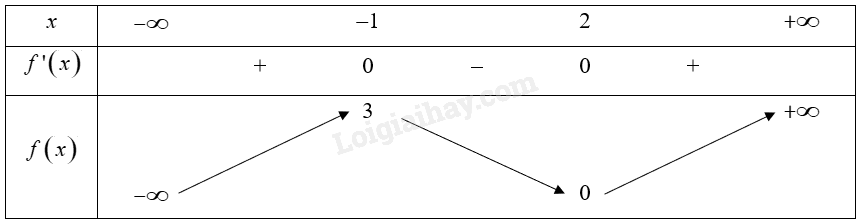
Điểm cực đại của hàm số đã cho là:

A. ‒1.

B. 3.

C. 2.

D. 0.

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

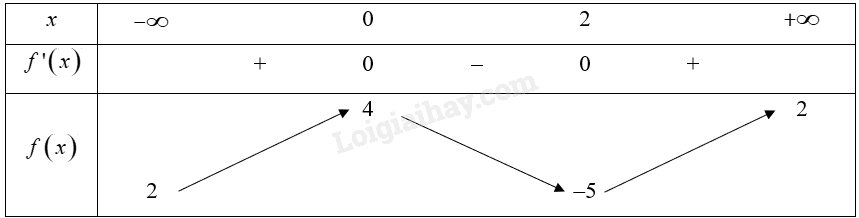
Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực tiểu tại $x =  - 5$.

B. Hàm số có giá trị cực đại bằng 0.

C. Hàm số đạt cực tiểu tại $x = 2$.

D. Hàm số đạt cực đại tại $x = 4$.

Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là:

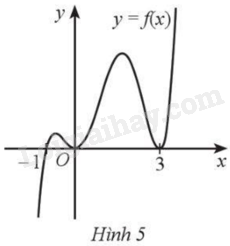
A. 2.                           

B. 4.

C. 1.

D. 3.

Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là:

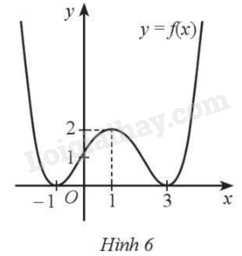
A. 2.

B. 1.

C. ‒1.

D. 0.

Cho hàm số $y = f\left( x \right)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như sau:

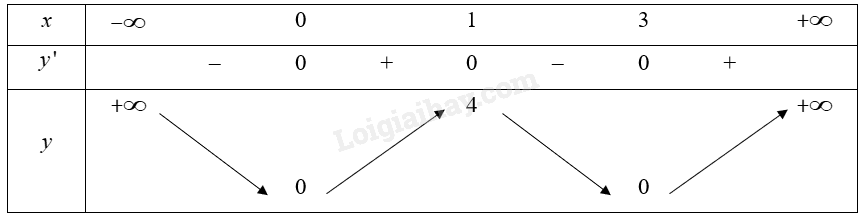
Số điểm cực trị của hàm số là:

A. 0.                                  

B. 1.                                  

C. 2.                                  

D. 3.

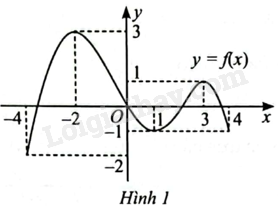
Hàm số $y = f\left( x \right)$ trong Hình 1 có bao nhiêu điểm cực trị?

A. 2.

B. 3.

C. 4.

D. 5.

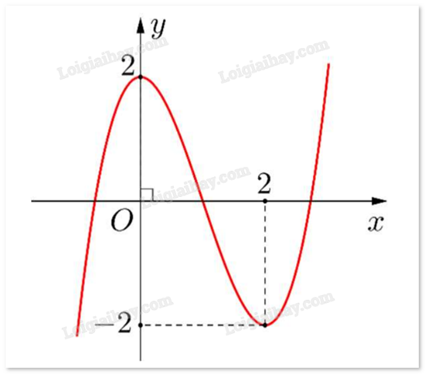
Cho hàm số y = f(x) có đồ thị như hình vẽ. Hàm số đạt cực tiểu tại

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.

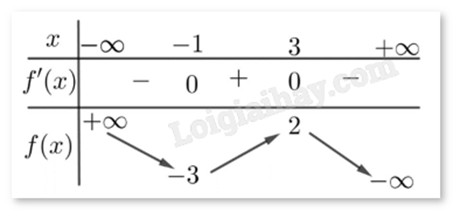
Điểm cực đại của hàm số đã cho là

Cho hàm số f(x) có đồ thị y = f’(x) như hình.

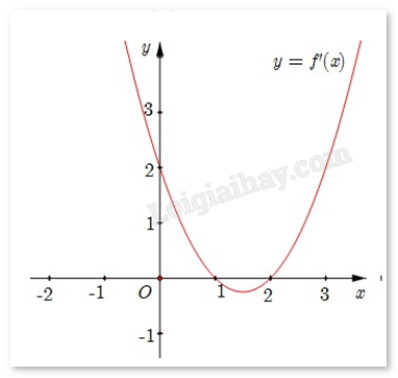
Hàm số f(x) có cực tiểu là

Cho hàm số y = f(x) có đồ thị như hình vẽ.

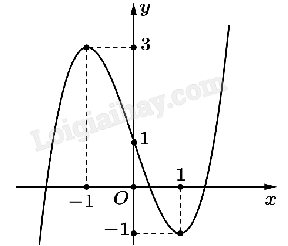
Điểm cực đại của hàm số đã cho là

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.

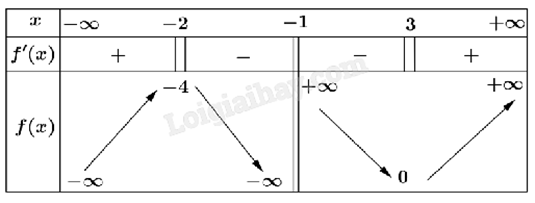
Điểm cực đại của hàm số đã cho là

Cho hàm số f(x) liên tục trên $\mathbb{R}$ và có bảng xét dấu f’(x) như sau:

Số điểm cực đại của hàm số đã cho là

Cho hàm số f(x) có bảng biến thiên như sau:

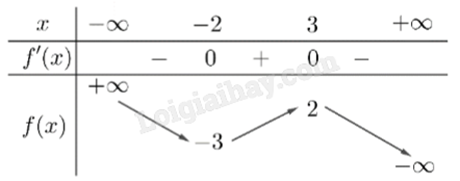
Giá trị cực đại của hàm số đã cho bằng

Cho hàm số y = f(x) liên tục trên  và có bảng xét dấu của f’(x) như hình dưới:

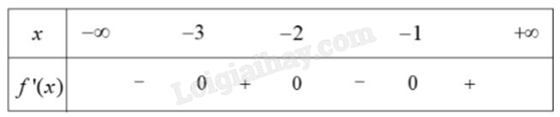
Hàm số y = f(x) có bao nhiêu điểm cực trị?

Cho hàm số bậc ba có bảng biến thiên như hình vẽ dưới đây.

Giá trị cực tiểu của hàm số là