Nội dung từ Loigiaihay.Com
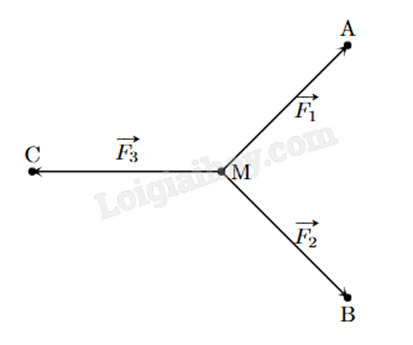
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
Đáp án:
Đáp án:
Sử dụng quy tắc tổng hợp lực, quy tắc hình bình hành.
Dựng hình bình hành AMBD. Vì \(\widehat {AMB} = {90^o}\) nên AMBD là hình vuông.
Áp dụng quy tắc hình bình hành, ta có \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MD} \).
Vì vật đứng yên nên \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
Từ đó ta suy ra \(\overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow 0 \) hay \(\overrightarrow {MD} = - \overrightarrow {MC} \). Khi đó \(\left| {\overrightarrow {MD} } \right| = \left| { - \overrightarrow {MC} } \right|\) tức MD = MC.
Vì MD là đường chéo của hình vuông cạnh 100 nên \(MD = 100\sqrt 2 \).
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = 100\sqrt 2 \approx 141\) N.













