Nội dung từ Loigiaihay.Com
Cho tam giác ABC đều cạnh bằng a. Tính \(\overrightarrow {AB} .\overrightarrow {BC} \).
-
A.
\(\overrightarrow {AB} .\overrightarrow {BC} = \frac{{{a^2}\sqrt 3 }}{2}\)
-
B.
\(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}\sqrt 3 }}{2}\)
-
C.
\(\overrightarrow {AB} .\overrightarrow {BC} = \frac{{{a^2}}}{2}\)
-
D.
\(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
Công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Ta có: \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = BA.BC\cos \widehat {ABC} = a.a\cos {60^o} = \frac{{{a^2}}}{2}\).
Suy ra \(\overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {BA} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\).
Đáp án : D

Các bài tập cùng chuyên đề
Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a,b,c.
Khi nào thì \({\left( {\overrightarrow u .\;\overrightarrow v } \right)^2} = {\left( {\overrightarrow u } \right)^2}.{\left( {\overrightarrow v } \right)^2}\)?
Khi nào thì tích vô hướng của hai vectơ \(\overrightarrow u ,\;\overrightarrow v \) là một số dương? Là một số âm?
Nếu hai điểm M, N thỏa mãn \(\overrightarrow {MN} .\overrightarrow {NM} = - 4\) thì độ dài đoạn thẳng MN bằng bao nhiêu?
A. MN = 4
B. MN = 2
C. MN = 16
D. MN = 256
Phát biểu nào sau đây là đúng?
A. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) < {90^o}\) thì \(\overrightarrow a .\overrightarrow b < 0\)
B. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) > {90^o}\) thì \(\overrightarrow a .\overrightarrow b > 0\)
C. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) < {90^o}\) thì \(\overrightarrow a .\overrightarrow b > 0\)
D. Nếu \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \) và \((\overrightarrow a ,\overrightarrow b ) \ne {90^o}\) thì \(\overrightarrow a .\overrightarrow b < 0\)
Tính \(\overrightarrow a .\overrightarrow b \) trong mỗi trường hợp sau:
a) \(\left| {\overrightarrow a } \right| = 3,\;\left| {\overrightarrow b } \right| = 4,\;(\overrightarrow a ,\overrightarrow b ) = {30^o}\)
b) \(\left| {\overrightarrow a } \right| = 5,\;\left| {\overrightarrow b } \right| = 6,\;(\overrightarrow a ,\overrightarrow b ) = {120^o}\)
c) \(\left| {\overrightarrow a } \right| = 2,\;\left| {\overrightarrow b } \right| = 3,\;\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
d) \(\left| {\overrightarrow a } \right| = 2,\;\left| {\overrightarrow b } \right| = 3,\;\overrightarrow a \) và \(\overrightarrow b \) ngược hướng
Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \)
b) \(\overrightarrow {AC} .\overrightarrow {BD} \)
Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
a) \(\overrightarrow {CB} .\overrightarrow {BA} \)
b) \(\overrightarrow {AH} .\overrightarrow {BC} \)
Cho tam giác ABC vuông tại A có \(\widehat B = {30^o},AB = 3\;cm.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} ;\;\overrightarrow {CA} .\overrightarrow {CB} .\)
Một người dùng một lực \(\overrightarrow F \) có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với \(\overrightarrow F \). Tính công sinh bởi lực \(\overrightarrow F \).
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có độ dài lần lượt là 3 và 8 có tích vô hướng là \(12\sqrt 2 \).Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng \(\sqrt 2 \).
Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {BC} ,\overrightarrow {BA} .\overrightarrow {BC} \)
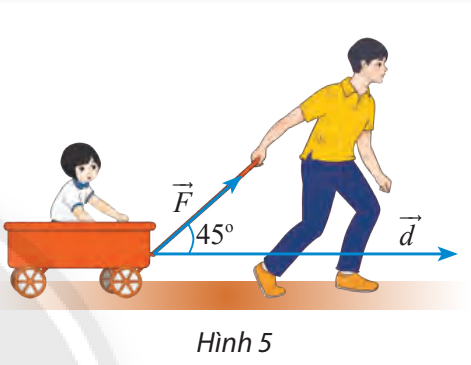
Một người dùng một lực \(\overrightarrow F \) có cường độ là 10 N kéo một chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực \(\overrightarrow F \), biết rằng góc giữa vectơ \(\overrightarrow F \) và hướng di chuyển là \(45^\circ \). (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực \(\overrightarrow F \), độ dài quãng đường và côsin các góc giữa vectơ \(\overrightarrow F \) và độ dịch chuyển \(\overrightarrow d \)).
Cho tam giác vuông cân ABC có \(AB = AC = a\).
Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} \).
Cho hình chữ nhật ABCD có tâm O và cho \(AD = 2a,AB = a\). Tính:
a) \(\overrightarrow {AB} .\overrightarrow {AO} \)
b) \(\overrightarrow {AB} .\overrightarrow {AD} \)
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ-không. Khẳng định nào sau đây là đúng?
Cho tam giác ABC có: AB = 3, BC = 4, AC = 5. Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).
Cho tam giác ABC có \(\widehat {ABC} = {30^o}\), AB = 5, BC = 8. Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).
Cho hai vecto \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \), \(\alpha \) là góc tạo vởi hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Chọn khẳng định đúng.












