Nội dung từ Loigiaihay.Com
Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC với A(-3;6), B(9;-10) và G\(\left( {\frac{1}{3};0} \right)\). Tọa độ điểm C là
-
A.
C(5;-4)
-
B.
C(5;4)
-
C.
C(-5;4)
-
D.
C(-5;-4)
Tọa độ điểm G là trọng tâm tam giác ABC là \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\)
Ta có \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}{x_c} = 3{x_G} - {x_A} - {x_B} = 3.\frac{1}{3} + 3 - 9 = - 5\\{y_c} = 3{y_G} - {y_A} - {y_B} = 3.0 - 6 + 10 = 4\end{array} \right.\)
Vậy C(-5;4).
Đáp án : C

Các bài tập cùng chuyên đề
Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có
\(\overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {OC} = 3\overrightarrow {OG} \).
Cho tam giác ABC có G là trọng tâm. Chứng minh \(\overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:
a) \(\overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AN} \)
b) \(\overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BA} \)
Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm tam giác BCD. Chứng minh:
a) \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} \)
b) \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Điểm G thuộc đoạn thẳng AE và \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Cho ABCD là hình bình hành. Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b .\) Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto \(\overrightarrow {AG} ,\overrightarrow {CG} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b .\)
Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:
a) \(\overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {MB} = \overrightarrow 0 \)
b) \(\overrightarrow {ND} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
c) \(\overrightarrow {PM} + \overrightarrow {PN} = \overrightarrow 0 \)
Phương pháp
a) Sử dụng tính chất trọng tâm của tam giác \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)(với G là trọng tâm của tam giác ABC)
b) Sử dụng tính chất trọng tâm của tam giác \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
c) Sử dụng tính chất trung điểm \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)(với M là trung điểm của AB)
a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết \(\overrightarrow {MB} = - \overrightarrow {MA} = \overrightarrow {AM} .\) Hoàn thành phép cộng vectơ sau: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AM} = \overrightarrow {MM} = ?\)
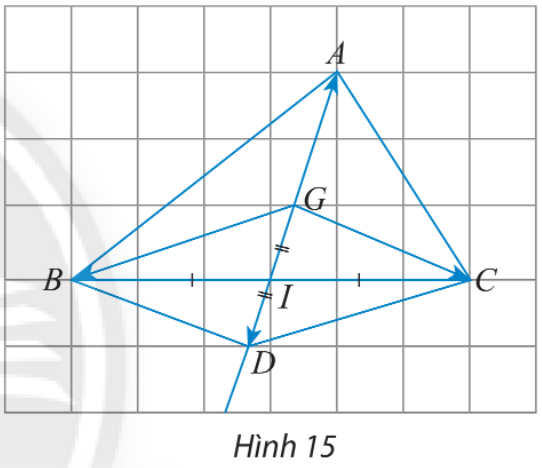
b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \) và \(\overrightarrow {GA} = \overrightarrow {DG} \), hoàn thành các phép cộng vectơ sau:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {{\rm{DD}}} = ?\)
Cho tam giác ABC có M thỏa mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \vec 0\). Xác định vị trí điểm M.
A. M thỏa mãn hình bình hành ACBM.
B. M là trung điểm của đoạn thẳng AB.
C. M trùng với C.
D. M là trọng tâm tam giác ABC.
Cho hình bình hành \(ABCD\) tâm \(O.\) \(M\) là một điểm tùy ý thuộc cạnh \(BC,\) khác \(B\) và \(C.\) \(MO\) cắt cạnh \(AD\) tại \(N.\)
a) Chứng minh rằng \(O\) là trung điểm của \(MN.\)
b) Gọi \(G\) là trọng tâm của tam giác \(BCD.\) Chứng minh rằng \(G\) cũng là trọng tâm tam giác \(MNC.\)
Trên cạnh \(BC\) của tam giác \(ABC\) lấy các điểm \(M,\,\,N,\) không trùng với \(B\) và \(C\) sao cho \(BM = MN = NC.\)
a) Chứng minh rằng hai tam giác \(ABC\) và \(AMN\) có cùng trọng tâm.
b) Gọi \(G\) là trọng tâm của tam giác \(ABC.\) Đặt \(\overrightarrow {GB} = \overrightarrow u \) và \(\overrightarrow {GC} = \overrightarrow v .\) hãy biểu thị các vectơ sau qua hai vectơ \(\overrightarrow u \) và \(\overrightarrow v :\,\,\overrightarrow {GA} ,\,\,\overrightarrow {GM} ,\,\,\overrightarrow {GN} .\)
Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để điểm M là trung điểm của đoạn thẳng AB là:
A. \(\overrightarrow {MA} = \overrightarrow {MB} \)
B. \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\)
C. \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng
D. \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)
Cho tam giác ABC. Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là:
A. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} \)
B. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \)
C. \(\overrightarrow {GC} + \overrightarrow {GA} = \overrightarrow {GB} \)
D. \(\overrightarrow {GA} + \overrightarrow {GB} - \overrightarrow {GC} = \overrightarrow 0 \)
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \).
Cho đoạn thẳng AB và O là trung điểm của AB. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} = 2\overrightarrow {OA} \)
B. \(\overrightarrow {AB} = 2\overrightarrow {OB} \)
C. \(\overrightarrow {AB} = - 2\overrightarrow {OB} \)
D. \(\overrightarrow {AO} = 2\overrightarrow {AB} \)
Cho tam giác ABC và M là trung điểm của BC, G là trọng tâm của tam giác. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AM} = - 3\overrightarrow {GM} \)
B. \(\overrightarrow {AM} = \frac{3}{2}\overrightarrow {GM} \)
C. \(\overrightarrow {AM} = - \frac{3}{2}\overrightarrow {GM} \)
D. \(\overrightarrow {AM} = 3\overrightarrow {GM} \)
Cho tam giác ABC và G là trọng tâm của tam giác. Với mỗi điểm M, chứng minh rằng:
\(M{A^2} + M{B^2} + M{C^2} = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\) (*)
Cho hình thoi ABCD và M là trung điểm của cạnh AB, N là trung điểm cạnh CD. Chứng minh rằng:
\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} = \overrightarrow {MN} \)
Cho hình vuông ABCD có tâm O và có cạnh bằng a. Cho 2 điểm M, N thỏa mãn:
\(\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 ;\overrightarrow {NB} + \overrightarrow {ND} + \overrightarrow {NC} = \overrightarrow 0 \).
Tìm độ dài các vectơ \(\overrightarrow {MA} ,\overrightarrow {NO} \).
Lấy một điểm M tùy ý. Chứng minh rằng:
a) I là trung điểm của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \)
b) G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Cho hai điểm phân biệt A và B. Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:
A. \(IA = IB\)
B. \(\overrightarrow {IA} = \overrightarrow {IB} \)
C. \(\overrightarrow {IA} = - \overrightarrow {IB} \)
D. \(\overrightarrow {AI} = \overrightarrow {BI} \)
Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {GA} = 2\overrightarrow {GI} \)
B. \(\overrightarrow {IG} = - \frac{1}{3}\overrightarrow {IA} \)
C. \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GI} \)
D. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} \)
Cho tam giác QRS có tọa độ các đỉnh \(Q\left( {7; - 2} \right),R( - 4;9)\) và \(S(5;8)\)
a) Tìm tọa độ trung điểm M của cạnh QS
b) Tìm tọa độ trọng tâm G của tam giác QRS
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh là \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là trung điểm của đoạn thẳng AB, \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm của tam giác ABC
a) Biểu thị vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
b) Biểu thị vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \)
c) Từ các kết quả trên, tìm tọa độ điểm M, G theo tọa độ của các điểm A, B, C
Cho tam giác ABC có các điểm \(M\left( {2;2} \right),N\left( {3;4} \right),P\left( {5;3} \right)\) lần lượt là trung điểm của các cạnh AB, BC và CA.
a) Tìm tọa độ các đỉnh của tam giác.
b) Chứng minh rằng trọng tâm của các tam giác ABC và MNP trùng nhau.
c) Giải tam giác ABC.
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).
a) Tìm toạ độ điểm M sao cho\(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) .
b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh\(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \) .
Cho hai điểm A(2; 4) và M(5 ; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB.
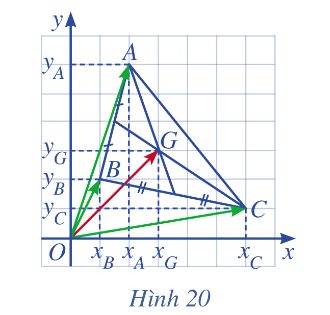
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trọng tâm G ( minh họa ở Hình 20)
a) Biểu diễn vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \).
b) Tìm tọa độ G theo tọa độ của A, B, C.
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2;0), N(4;2), P(1;3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3\)?
A. Vô số
B. 1
C. 2
D. 3
Cho G là trọng tâm của tam giác ABC và điểm M bất kỳ. Đẳng thức nào sau đây đúng?