Nội dung từ Loigiaihay.Com
Cho phương trình \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
a) Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\).
b) Sử dụng công thức \(\cos (x + \pi ) = - \cos x\).
c) Sử dụng công thức hạ bậc \({\sin ^2}x = \frac{{1 - \cos 2x}}{2}\), \({\cos ^2}x = \frac{{\cos 2x + 1}}{2}\).
d) Sử dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
a) Đúng. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1 - {\cos ^2}\left( {2x + \frac{\pi }{4}} \right)\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = {\sin ^2}\left( {2x + \frac{\pi }{4}} \right)\).
b) Đúng. \(\cos (2x + \pi ) = - \cos 2x\).
c) Đúng. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = {\sin ^2}\left( {2x + \frac{\pi }{4}} \right)\)
\( \Leftrightarrow \frac{{\cos \left( {2x + \pi } \right) + 1}}{2} = \frac{{1 - \cos \left( {4x + \frac{\pi }{2}} \right)}}{2}\)
\( \Leftrightarrow \cos \left( {2x + \pi } \right) = - \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow - \cos 2x = - \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow \cos 2x = \cos \left( {4x + \frac{\pi }{2}} \right)\).
d) Sai. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1 \Leftrightarrow \cos 2x = \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = 4x + \frac{\pi }{2} + k2\pi \\2x = - 4x - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 4x + \frac{\pi }{2} + k2\pi \\2x = - 4x - \frac{\pi }{2} + k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l} - 2x = \frac{\pi }{2} + k2\pi \\6x = - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{4} + k\pi \\x = - \frac{\pi }{{12}} + k\frac{\pi }{3}\end{array} \right.\) \((k \in \mathbb{Z})\).

Các bài tập cùng chuyên đề
Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu \({v_0} = 500m/s\) hợp với phương ngang một góc \(\alpha \). Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình \(y = - \frac{g}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \), ở đó \(g = 9,8m/{s^2}\) là gia tốc trọng trường.
a) Tính theo góc bắn \(\alpha \) tầm xa mà quả đạn đạt tới (tức là khoảng cách từ vị trí bắn đến điểm quả đạn chạm đất).
b) Tìm góc bắn \(\alpha \) để quả đạn trúng mục tiêu cách vị trí đạt khẩu pháo 22 000m.
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình
\(x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\)
Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimet. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Tập xác định của hàm số \(y = \frac{{\cos x}}{{\sin x - 1}}\) là
A. \(\mathbb{R}\backslash \{ k2\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)
B. \(\mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k2\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)
C. \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)
D. \(\mathbb{R}\backslash \{ k\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)
Giải các phương trình sau:
a) \(\cos \left( {3x - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2}\);
b) \(2{\sin ^2}x - 1 + \cos 3x = 0\);
c) \(\tan \left( {2x + \frac{\pi }{5}} \right) = \tan \left( {x - \frac{\pi }{6}} \right)\).
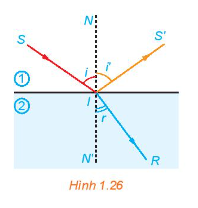
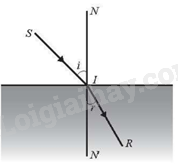
Khi một tia sáng truyền từ không khi vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới i liên hệ với góc khúc xạ r bởi Định luật khúc xạ ánh sáng
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\)
Ở đây, \({n_1}\) và \({n_2}\) tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới \(i = {50^0}\), hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33.
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ \(40^\circ \) Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số:\(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\)
a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?
b) Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?
c) Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?
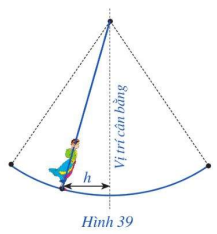
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 39). Nghiên cứu trò chơi này, người ta thấy khoảng cách h (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với \(t \ge 0\)) bởi hệ thức \(h = \left| d \right|\) với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại. Vào thời gian t nào thì khoảng cách h là 3m; 0m?
Giải các phương trình sau:
a) \(\sin \left( {2x - \frac{\pi }{6}} \right) = - \frac{{\sqrt 3 }}{2}\)
b) \(\cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \frac{1}{2}\)
c) \(\sin 3x - \cos 5x = 0\)
d) \({\cos ^2}x = \frac{1}{4}\)
e) \(\sin x - \sqrt 3 \cos x = 0\)
f) \(\sin x + \cos x = 0\)
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày \(\left( {0 \le t < 24} \right)\) cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\). Tìm t để độ sâu của mực nước là
a) 15m
b) 9m
c) 10,5m
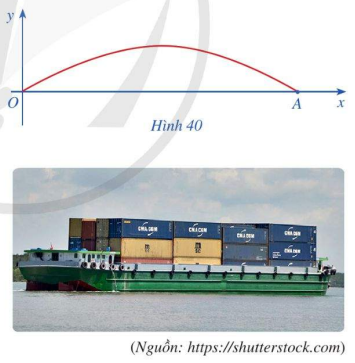
Một cây cầu có dạng cung OA của đồ thị hàm số \(y = 4,8\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 40.
a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (Làm tròn kết quả đến hàng phần mười)
b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1m.
c) Một sà lan khác cũng chở khối hàng hóa được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hóa đó là 9m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hóa đó phải nhỏ hơn 4,3m
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức: \(h(t) = 29 + 3sin\frac{\pi }{{12}}(t - 9)\;\) với h tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ?
(Theo https://www.sciencedirect.com/science/article/abs/pii/0168192385900139)
A. \({32^o}C\), lúc 15 giờ
B. \({29^o}C\), lúc 9 giờ
C. \({26^o}C\), lúc 3 giờ
D. \({26^o}C\), lúc 0 giờ
Giải các phương trình sau:
\(\begin{array}{l}a)\;sin2x + cos3x = 0\\b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\c)\;sinx + sin2x = 0\end{array}\)
Độ sâu h (m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thuỷ triểu lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức \(h(t) = 0,8cos0,5t + 4.\)
(Theo https://noc.ac.uk/files/documents/business/an-introduction-to-tidal-modelling.pdf)
a) Độ sâu của nước vào thời điểm t = 2 là bao nhiêu mét?
b) Một con tàu cần mực nước sâu tối thiểu 3,6 m để có thể di chuyển ra vào cảng an toàn. Dựa vào đồ thị của hàm số côsin, hãy cho biết trong vòng 12 tiếng đầu tiên sau khi thuỷ triểu lên lần đầu tiên, ở những thời điểm t nào tàu có thể hạ thuỷ. Làm tròn kết quả đến hàng phần trăm.
Cho vận tốc \(v{\rm{ }}\left( {cm/s} \right)\) của một con lắc đơn theo thời gian t (giây) được cho bởi công thức \(v = - 3sin\left( {1,5t + \frac{\pi }{3}} \right).\)
Xác định các thời điểm t mà tại đó:
a) Vận tốc con lắc đạt giá trị lớn nhất
b) Vận tốc con lắc bằng 1,5 cm/s
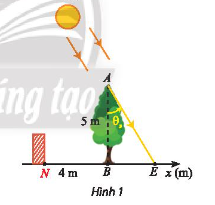
Trong Hình 1, cây xanh AB nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5 m. Bóng của cây là BE. Vào ngày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Góc thiên đỉnh \({\theta _t} = (AB,AE)\) phụ thuộc vào vị trí của Mặt trời và thay đổi theo thời gian trong ngày theo công thức \({\theta _s}(t) = (AB,AE) = \frac{\pi }{{12}}(t - 12)\;\) rad với t là thời gian trong ngày (theo đơn vị giờ, 6 < t < 18).
(Theo https://www.sciencedirect.com/topics/engineering/solar-hour-angle)
a) Viết hàm số biểu diễn toạ độ của điểm E trên trục Bx theo t.
b) Dựa vào đồ thị hàm số tang, hãy xác định các thời điểm mà tại đó bóng cây phủ qua vị trí tường rào N biết N nằm trên trục Bx với toạ độ là \({x_N} = - 4\;\) (m). Làm tròn kết quả đến hàng phần mười.
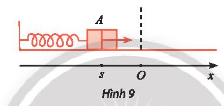
Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức \(s = 10sin\left( {10t + \frac{\pi }{2}} \right).\)Vào các thời điểm nào thì \(s = - 5\sqrt 3 \;\)cm?
Trong Hình 10, ngọn đèn trên hải đăng H cách bờ biển yy' một khoảng HO = 1 km. Đèn xoay ngược chiều kim đồng hồ với tốc độ \(\frac{\pi }{{10}}\)rad/s và chiếu hai luồng ánh sáng về phía đối diện nhau. Khi đèn xoay, điểm M mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển dộng dọc theo bờ.
(Theo https://www.mnhs.org/splitrock/learn/technology)

a) Ban đầu luồng sáng trùng với đường thẳng HO. Viết hàm số biểu thị toạ độ \({y_M}\) của điểm M trên trục Oy theo thời gian t.
b) Ngôi nhà N nằm trên bờ biển với toạ độ \({y_N} = - 1\;\left( {km} \right).\) Xác định các thời điểm t mà đèn hải đăng chiếu vào ngôi nhà.
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 3\cos \left( {4\pi t - \frac{{2\pi }}{3}} \right)\), với \(t\) là thời gian tính bằng giây và \(x\) là quãng đường tính bằng cm. Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
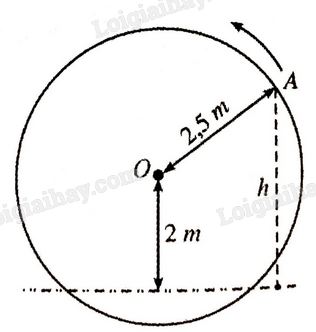
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là \(h = \left| y \right|\) trong đó \(y = 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right)\) với x là thời gian quay của guồng \(\left( {x \ge 0} \right),\) tính bằng phút; ta quy ước rằng \(y > 0\) khi gầu ở trên mặt nước và \(y < 0\) khi gầu ở dưới mặt nước.
a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?
b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ ngày 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số:
\(L\left( t \right) = 12 + 2,83\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right)\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\)
a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?
b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?
Huyết áp là áp lực cần thiết tác dụng lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi là huyết áp tâm thu và tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử một người nào đó có nhịp tim là 70 lần trên phút và huyết áp của người đó được mô hình hóa bởi hàm số \(P\left( t \right) = 100 + 20\sin \left( {\frac{{7\pi }}{3}t} \right)\), ở đó P(t) là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian tính theo giây.
a) Trong khoảng từ 0 giây đến 1 giây, hãy xác định số lần huyết áp là 100mmHg.
b) Trong khoảng từ 0 giây đến 1 giây, hãy xác định số lần huyết áp là 120mmHg.
Giá trị của \(m\) để phương trình \(\cos x = m\) có nghiệm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là:
A. \(0 \le m < 1\)
B. \(0 \le m \le 1\)
C. \(0 < m \le 1\)
D. \(0 < m < 1\)
Mực nước cao nhất tại một cảng biển là 16 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều xuống thấp thì mực nước thấp nhất là 10 m. Đồ thị ở hình bên mô tả sự thay đổi chiều cao của mực nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước \(h\) (m) theo thời gian \(t\)(h) \(\left( {0 \le t \le 24} \right)\) được cho bởi công thức \(h = m + a\cos \left( {\frac{\pi }{{12}}t} \right)\) với \(m\), \(a\) là các số thực dương cho trước.
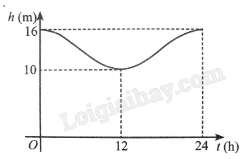
a) Tìm \(m\), \(a\).
b) Tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m.
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số \(\frac{{\sin i}}{{\sin r}}\), với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là \({45^o}\) thì góc khúc xạ bằng \({30^o}\). Khi góc tới là \({60^o}\) thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.
Một quả bóng được ném xiên một góc \(\alpha \left( {{0^0} \le \alpha \le {{90}^0}} \right)\) từ mặt đất với tốc độ \({v_0}\left( {m/s} \right)\). Khoảng cách theo phương ngang từ vị trí ban đầu của quả bóng đến vị trí bóng chạm đất được tính bởi công thức \(d = \frac{{v_0^2\sin 2\alpha }}{{10}}\).
a) Tính khoảng cách d khi bóng được ném đi với tốc độ ban đầu 10m/s và góc ném là \({30^0}\) so với phương nằm ngang.
b) Nếu tốc độ ban đầu của bóng là 10m/s thì cần ném bóng với góc bao nhiêu độ để khoảng cách d là 5m?
Chiều cao h(m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức \(h\left( t \right) = 30 + 20\sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right)\).
a) Cabin đạt độ cao tối đa là bao nhiêu?
b) Sau bao nhiêu giây thì cabin đạt độ cao 40m lần đầu tiên?
Vận tốc \({v_1}\left( {cm/s} \right)\) của con lắc đơn thứ nhất và vận tốc \({v_2}\left( {cm/s} \right)\) của con lắc đơn thứ hai theo thời gian t (giây) được cho bởi các công thức:
\({v_1}\left( t \right) \) \( = - 4\cos \left( {\frac{{2t}}{3} + \frac{\pi }{4}} \right)\) và \({v_2}\left( t \right) \) \( = 2\sin \left( {2t + \frac{\pi }{6}} \right)\)
Xác định các thời điểm t mà tại đó:
a) Vận tốc của con lắc đơn thứ nhất bằng 2cm/s.
b) Vận tốc của con lắc đơn thứ nhất gấp hai lần vận tốc của con lắc đơn thứ hai.
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ $t$ của năm $2017$ được cho bởi một hàm số $y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10$ với $t \in \mathbb{Z}$ và $0 < t \leqslant 365$. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị tri cân bằng. Giả sử khoảng cách \(h\) (tính bằng mét) từ người chơi đu đến vị trí cân bằng được tính theo thời gian \(t(t \ge 0\) và được tính bằng giây) bởi hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\), trong đó ta quy ước rằng \(d > 0\) khi vị trí cân bằng ở về phía sau lưng người chơi đu và \(d < 0\) trong trường hợp ngược lại.
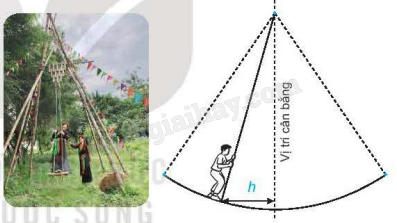
a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.
b) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 m (tính chính xác đến 0,01 giây).












