Hàm số \(y = \frac{1}{{2x - 4}}\) gián đoạn tại điểm nào dưới đây?

Bài 1 :

Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{x + 1 + \sqrt[3]{{x - 1}}}}{x}{\rm{ khi }}x \ne 0\\ \frac{4}{3}{\rm{                   khi }}x = 0\end{array} \right.\). Khẳng định nào sau đây đúng nhất :

Bài 2 :

Hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{1 + \cos x\,\,\,\,{\rm{ khi }}\,\,\,\sin x \ge 0}\\{3 - \cos x\,\,\,\,{\rm{ khi }}\,\,\,\sin x < 0}\end{array}} \right.\) có bao nhiêu điểm gián đoạn trên khoảng \(\left( {0;2019} \right)\)?

Bài 3 :

Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{ - x\;,x < 0}\\{0\;,\;x = 0}\\{{x^2},x > 0}\end{array}} \right.\) tại điểm \({x_0} = 0\).

Bài 4 :

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 1}}{{x - 1}},\;x \ne 1}\\{2\;,\;x = 1}\end{array}} \right.\)

Tính giới hạn \(\mathop {{\rm{lim}}}\limits_{x \to 1} f\left( x \right)\) và so sánh giá trị này với \(f\left( 1 \right)\).

Bài 5 :

Tìm giá trị của tham số m đề hàm số

\(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\sin x\;,x \ge 0}\\{ - x + m\;\;,\;x < 0}\end{array}} \right.\)    liên tục trên \(\mathbb{R}\)

Bài 6 :

Cho hàm số \(\left\{ \begin{array}{l}\frac{{{x^2} + x - 2}}{{x - 1}},x \ne 1\\a,x = 1\end{array} \right.\). Hàm số \(f\left( x \right)\) liên tục tại \(x = 1\) khi

A. \(a = 0\)                  

B. \(a = 3\)                  

C. \(a =  - 1\)               

D. \(a = 1\)

Bài 7 :

Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho

a) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{1}{x},\;x \ne 0}\\{1\;,\;x = 0}\end{array}} \right.\;\;\)gián đoạn tại \(x = 0\)

b) \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 + x\;,\;x < 1}\\{2 - x\;,x \ge 1}\end{array}} \right.\;\;\)gián đoạn tại \(x = 1\)

Bài 8 :

Tìm các giá trị của a để hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1\;,x \le a}\\{{x^2},\;a > a}\end{array}} \right.\) liên tục trên \(\mathbb{R}\)

Bài 9 :

Xét tính liên tục của hàm số \(f\left( x \right) = {x^3} + 1\) tại \({x_0} = 1.\)

Bài 10 :

Quan sát đồ thị hàm số \(f\left( x \right) = x\) ở Hình 11.

a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\)

b) So sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) với \(f\left( 1 \right).\)

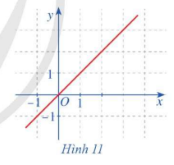
Bài 11 :

Dùng định nghĩa xét tính liên tục của hàm số \(f\left( x \right) = 2{x^3} + x + 1\) tại điểm \(x = 2.\)

Bài 12 :

Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\) và \({x_0} \in (a;b)\). Điều kiện cần và đủ để hàm số \(y = f(x)\) liên tục tại \({x_0}\) là:

A. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = f\left( {{x_0}} \right)\).                                    

B. \(\mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).

C. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x)\).                              

D. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).

Bài 13 :

Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\) và \({x_0} \in (a;b)\). Điều kiện cần và đủ để hàm số \(y = f(x)\) liên tục tại \({x_0}\) là:

A. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = f\left( {{x_0}} \right)\).                                    

B. \(\mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).

C. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x)\).                              

D. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).

Bài 14 :

Xét tính liên tục của hàm số:

a) \(f\left( x \right) = 1 - {x^2}\) tại điểm \({x_0} = 3\);  

b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x > 1}\\{ - x}&{khi\,\,x \le 1}\end{array}} \right.\) tại điểm \({x_0} = 1\).

Bài 15 :

Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.

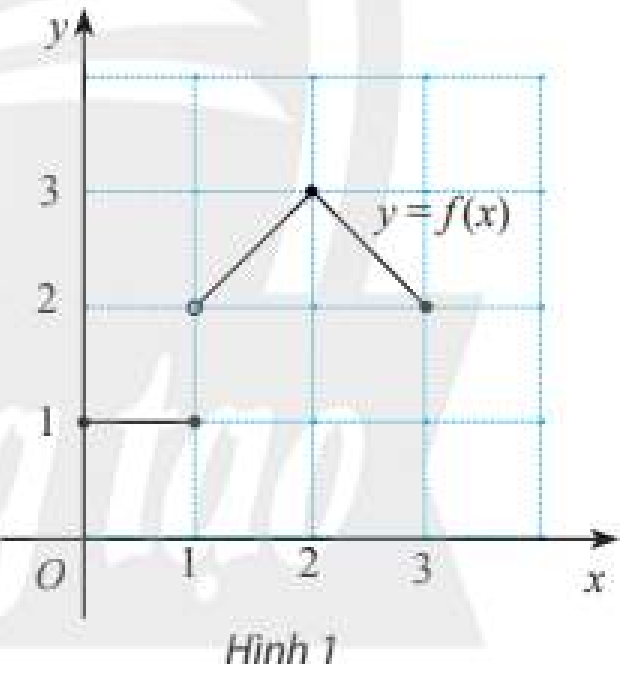
Tại mỗi điểm \({x_0} = 1\) và \({x_0} = 2\), có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không? Nếu có, giới hạn đó có bằng \(f\left( {{x_0}} \right)\) không?

Bài 16 :

Xét tính liên tục của hàm số:

a) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x \ge 0}\\{1 - x}&{khi\,\,x < 0}\end{array}} \right.\) tại điểm \(x = 0\).

b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 2}&{khi\,\,x \ge 1}\\x&{khi\,\,x < 1}\end{array}} \right.\) tại điểm \(x = 1\).

Bài 17 :

Hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 2{\rm{x}} + m}&{khi\,\,x \ge 2}\\3&{khi\,\,x < 2}\end{array}} \right.\) liên tục tại \(x = 2\) khi:

A. \(m = 3\).                            

B. \(m = 5\).                            

C. \(m =  - 3\).                         

D. \(m =  - 5\).

Bài 18 :

Dùng định nghĩa, xét tính liên tục của hàm số:

a) \(f\left( x \right) = {x^3} - 3x + 2\) tại điểm \(x =  - 2\);

b) \(f\left( x \right) = \sqrt {3x + 2} \) tại điểm \(x = 0\).

Bài 19 :

Xét tính liên tục của mỗi hàm số sau tại điểm \(x = 2\):

a) \(f\left( x \right) = \left\{ \begin{array}{l}6 - 2x\;\;\;khi\;x \ge 2\\2{x^2} - 6\;\;khi\;x < 2\end{array} \right.\);

b) \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 4}}{{x - 2}}\;\;\;khi\;x \ne 2\\\;\;\;\;0\;\;\;\;\;\;khi\;x = 2\end{array} \right.\).

Bài 20 :

Xét tính liên tục của hàm số:

a) \(f\left( x \right) = \left| {x + 1} \right|\) tại điểm \(x =  - 1\);

b) \(g\left( x \right) = \left\{ \begin{array}{l}\frac{{\left| {x - 1} \right|}}{{x - 1}}\;\;\;khi\;x \ne 1\\\;\;\;\;1\;\;\;\;\;\;khi\;x = 1\end{array} \right.\) tại điểm \(x = 1\).

Bài 21 :

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {x + 2}  - 2}}{{x - 2}}\;khi\;x \ne 2\\\;\;\;\;a\;\;\;\;\;\;\;\;\;\;\;khi\;x = 2\end{array} \right.\). Tìm giá trị của tham số a để hàm số \(y = f\left( x \right)\) liên tục tại \(x = 2\).

Bài 22 :

Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?

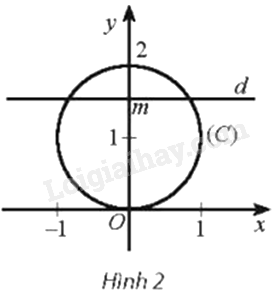
Bài 23 :

Biết rằng hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{2 - \sqrt {x + 1} }}{{x - 3}}\;\;khi\;x \ne 3\\\;\;\;\;\;\;\;a\;\;\;\;\;\;\;\;\,khi\;x = 3\end{array} \right.\)  liên tục tại điểm \(x = 3\). Giá trị của a bằng

A. \( - \frac{1}{4}\).

B. \(\frac{1}{4}\).

C. \( - 2\).

D. 3.

Bài 24 :

Phát biểu nào sau đây là đúng?

A. Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)\).

B. Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right)\).

C. Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)\).

D. Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right)\).

Bài 25 :

Cho đồ thị hàm số \(y = f\left( x \right)\) trong hình dưới đây. Phát biểu nào sau đây là SAI?

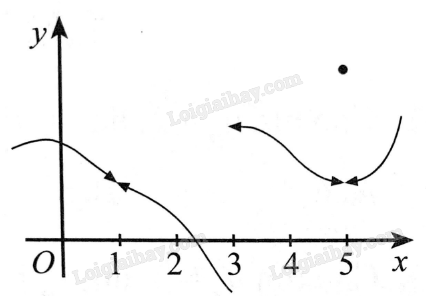
A. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 1\).

B. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 3\).

C. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 5\).

D. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 0\).

Bài 26 :

Cho hàm số g(x) liên tục trên \(\mathbb{R}\) trừ điểm \(x = 0\). Xét tính liên tục của hàm số \(f\left( x \right) = \frac{{g\left( x \right)}}{x}\) tại \(x = 1\).

Bài 27 :

Cho hàm số \(f(x) = \frac{{\sqrt {x - 1}  - \sqrt {1 - x} }}{x}\). Phải bổ sung thêm giá trị \(f(0)\) bằng bao nhiêu để hàm số \(f(x)\) liên tục tại \(x = 0\). 

Bài 28 :

Một điểm dịch vụ trông giữ xe ô tô thu phí 30 nghìn đồng trong giờ đầu tiên và thu thêm 20 nghìn đồng cho mỗi giờ tiếp theo.

a) Viết hàm số \(f(x)\) mô tả số tiền phí theo thời gian trông giữ.

b) Xét tính liên tục của hàm số này.

Bài 29 :

Hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây:

Hàm số gián đoạn tại điểm

Bài 30 :