Chọn khẳng định sai.

Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?

Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng

Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn

Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?

Số đo cung lớn \(BnC\) trong hình bên  là:

Chọn khẳng định đúng. Trong một đường tròn, số đo cung lớn bằng

Chọn câu đúng. Trong hai cung của một đường tròn hay hai đường tròn bằng nhau,

Cho đường tròn (O) đường kính $AB$ và một cung $AC$ có số đo bằng $50^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?

Tại sao số đo cung lớn của một đường tròn luôn lớn hơn \({180^0}\)

Cho điểm C nằm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A. Tính số đo của các cung \(\overset\frown{ACB}\) và \(\overset\frown{ABC}\).

Trên mặt một chiếc đồng hồ có các vạch chia như Hình 5.12. Hỏi cứ sau mỗi khoảng thời gian 36 phút:

a) Đầu kim phút vạch trên một cung có số đo bằng bao nhiêu độ?

b) Đầu kim giờ vạch trên một cung có số đo bằng bao nhiêu độ?

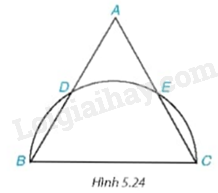
Cho tam giác đều ABC có AB = \({\rm{2}}\sqrt 3 \)cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).

a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.

b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.

Cho hình 5.43, trong đó BD là đường kính, \(\widehat {{\rm{AOB}}} = 40^\circ ;\widehat {\,{\rm{BOC}}} = 100^\circ \). Khi đó:

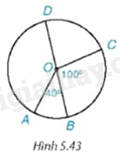
A. sđ \(\overset\frown{\text{DC}}=80{}^\circ \) và sđ \(\overset\frown{\text{AD}}=220{}^\circ \)

B. sđ \(\overset\frown{\text{DC}}=280{}^\circ \) và sđ \(\overset\frown{\text{AD}}=220{}^\circ \)

C. sđ \(\overset\frown{\text{DC}}=280{}^\circ \) và sđ \(\overset\frown{\text{AD}}=140{}^\circ \)

D. sđ \(\overset\frown{\text{DC}}=80{}^\circ \) và sđ \(\overset\frown{\text{AD}}=140{}^\circ \)

Tỉ lệ các loại quả bán được trong một ngày của một cửa hàng được thể hiện trong biểu đồ hình quạt tròn như hình bên. Số phần trăm ghi trong mỗi hình quạt đúng bằng tỉ số giữa số đo của cung tròn tương ứng và số đo của cả đường tròn \(\left( {{{360}^o}} \right)\).

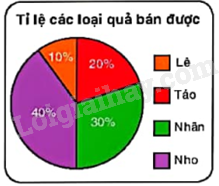
a) Tính số đo của mỗi cung tròn ứng với hình quạt màu tím, màu cam và màu đỏ.

b) Tính số đo của cung còn lại (ứng với hình quạt màu xanh) bằng hai cách.

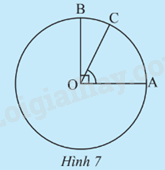
Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.

a) Xác định số đo cung AB.

b) So sánh số đo của hai cung \(\overset\frown{AC}\) và \(\overset\frown{AB}\)

Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung \(\overset\frown{AB}\),\(\overset\frown{AC}\) và \(\overset\frown{AD}\).

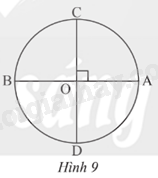
Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10).

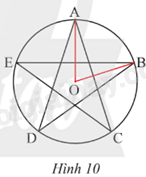
Trên đường tròn (O), vẽ hai cung nhỏ \(\overset\frown{AB}\); \(\overset\frown{BC}\) sao cho \(\widehat {AOB} = {18^o};\widehat {BOC} = {32^o}\) và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung \(\overset\frown{AB}\); \(\overset\frown{BC}\); \(\overset\frown{AC}\).

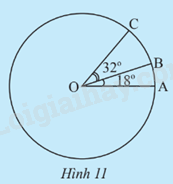
Trên cung AB có số đo 90^o của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15^o. Tính số đo của cung MB.

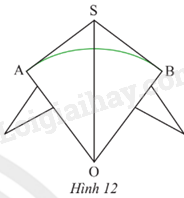
Bạn Hùng làm một cái diều với thân diều là hình tứ giác S.AOB sao cho OS là đường phân giác của \(\widehat {AOB}\) và \(\widehat {ASB} = {106^o}\). Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của \(\overset\frown{AB}\).

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung \(\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}\).

Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

a) Tính số đo mỗi cung

b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng \(\frac{{AB}}{2}\).

Cho hai đường tròn đồng tâm (O; R) và (O; \(\frac{{R\sqrt 3 }}{2}\)). Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.

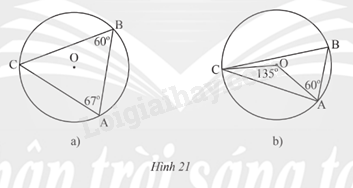
Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau:

Thành phố Đà Lạt nằm vào khoảng \({11^o}58'\) vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40000 km. Hãy tính độ dài cung kinh tuyến từ Đà Lạt đến xích đạo.

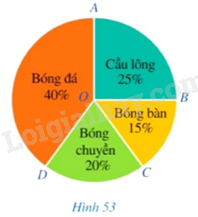
Trong Hình 53, tìm số đo của các góc ở tâm \(\widehat {BOC};\widehat {DOA}\).

Tiếp tuyến tại hai điểm A và B của đường tròn (O) cắt nhau tại M. Biết rằng MAB là tam giác đều. Tính số đo cung nhỏ và cung lớn AB.

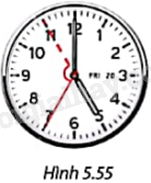
Trong 20 giây, kim giây của đồng hồ quay được một cung có số đo bằng bao nhiêu (Hình 5.55)?

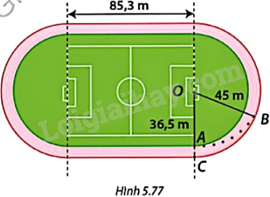
Trong Hình 5.77, mỗi làn chạy của sân vận động được thiết kế gồm hai phần là đường chạy thẳng và hai phần có dạng nửa đường tròn. Trong một cuộc thi điền kinh, vận động viên ở làn trong cùng xuất phát từ vị trí điểm A, chạy ngược chiều kim đồng hồ đúng một vòng và về đích ở điểm A.

a) Tính cự li chạy của cuộc thi (tổng quãng đường vận động viên phải chạy).

b) Để đảm bảo cự li chạy như nhau, vận động viên ở làn ngoài cùng không chạy đúng một vòng mà xuất phát từ vị trí điểm B và về đích ở điểm C. Xác định số đo góc COB.

Cho tam giác cân ABC (AB=AC). Gọi (O) là đường tròn đi qua ba điểm A, B, C và E là điểm trên cung nhỏ BC sao cho $\overset\frown{BE}=\overset\frown{EC}$.

a) Chứng minh rằng ba điểm A, O, E thẳng hàng.

b) Gọi H là chân đường cao hạ từ A xuống BC. Chứng minh rằng \(AH < AB < AE\).