Chứng minh rằng hàm số $f(x) = \left| x \right|$ không có đạo hàm tại điểm ${x_0} = 0$, nhưng có đạo hàm tại mọi điểm $x \ne 0$.

Với tình huống trong Hoạt động mở đầu, hãy tính vận tốc tức thời của chuyển động lúc $t = 2$.

Một chuyển động thẳng xác định bởi phương trình $s\left( t \right) = 4{t^3} + 6t + 2$, trong đó $s$ tính bằng mét và $t$ là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại $t = 2$.

Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức $h\left( t \right) = 0,81{t^2}$, với $t$ được tính bằng giây và $h$ tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt Trăng tại thời điểm $t = 2$.

(Nguồn: https://www.britannica.com/place/Moon)

Hàm số $y =  - {x^2} + x + 7$ có đạo hàm tại $x = 1$ bằng

A. ‒1.                     

B. 7.                       

C. 1.                        

D. 6.

Một viên soi rơi từ độ cao 44,1 m thì quãng đường rơi được biểu diễn bởi công thức $s\left( t \right) = 4,9{t^2}$, trong đó $t$ là thời gian tính bằng giây và $s$ tính bằng mét. Tinh:

a) Vận tốc rơi của viên sỏi lúc $t = 2$;

b) Vận tốc của viên sỏi khi chạm đất.

Một vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right) = 2{t^3} + 4t + 1$, trong đó $t$ là thời gian tính bằng giây và $s$ tính bằng mét.

Tính vận tốc và gia tốc của vật khi $t = 1$.

Dân số $P$ (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức $P\left( t \right) = \frac{{500t}}{{{t^2} + 9}}$, trong đó $t$ là thời gian được tính bằng năm. Tìm tốc độ tăng dân số tại thời điểm $t = 12$.

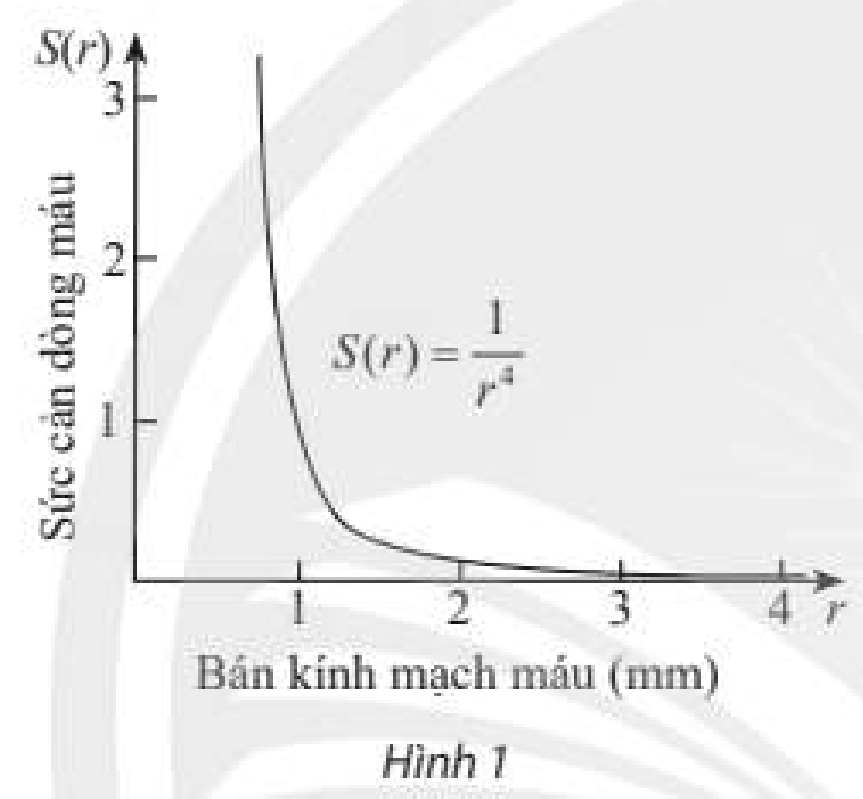
Hàm số $S\left( r \right) = \frac{1}{{{r^4}}}$ có thể được sử dụng để xác định sức cản $S$ của dòng máu trong mạch máu có bản kính $r$ (tính theo milimét) (theo Bách khoa toàn thu Y học Harrison's internal medicine 21st edition”). Tìm tốc độ thay đổi của $S$ theo $r$ khi $r = 0,8$.

Nhiệt độ cơ thể của một người trong thời gian bị bệnh được cho bởi công thức $T\left( t \right) =  - 0,1{t^2} + 1,2t + 98,6$, trong đó $T$ là nhiệt độ (tính theo đơn vị đo nhiệt độ Fahrenheit) tại thời điểm $t$ (tính theo ngày). Tìm tốc độ thay đổi của nhiệt độ ở thời điểm $t = 1,5$.

(Nguồn: https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.1111985.html)

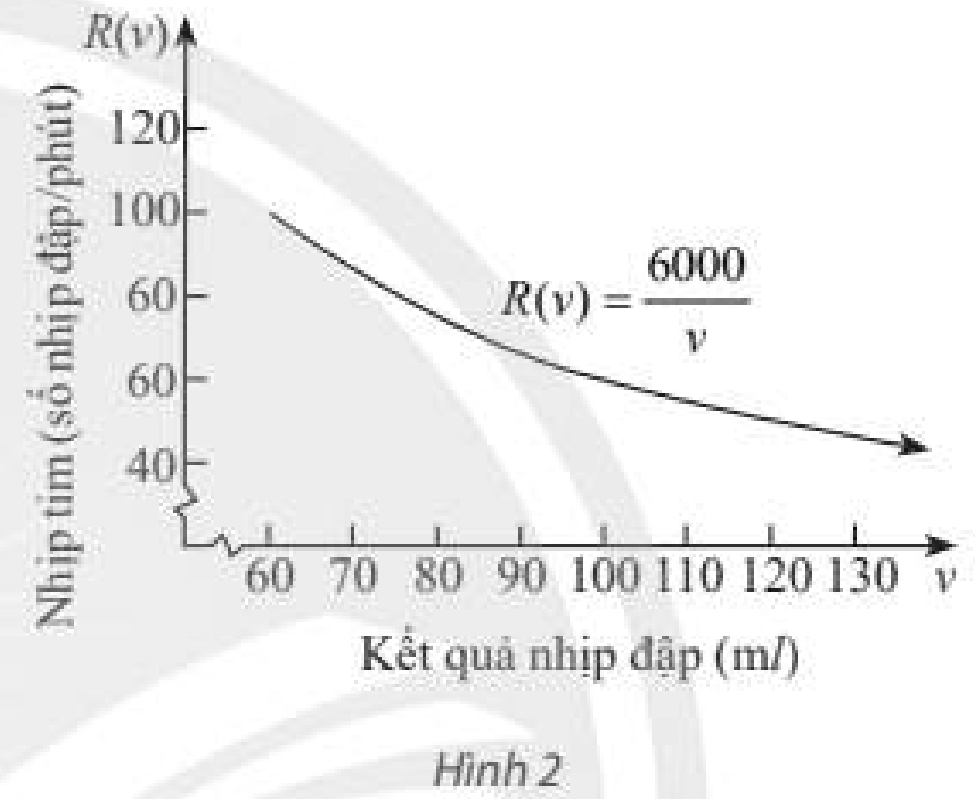
Hàm số $R\left( v \right) = \frac{{6000}}{v}$ có thể được sử dụng để xác định nhịp tim $R$ của một người mà tim của người đó có thể đây đi được $6000ml$ máu trên mỗi phút và $v{\rm{ }}ml$ máu trên mỗi nhịp đập (theo Bách khoa toàn thư Y học “Harrison's internal medicine 21st edition”). Tìm tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp là $v = 80$.

Một chuyển động thẳng xác định bởi phương trình $s\left( t \right) = 2{t^3} + 4t + 1$, trong đó $s$ tính bằng mét và $t$ là thời gian tính bằng giây.

a) Tính vận tốc tức thời $v\left( t \right)$ tại thời điểm $t$.

b) Đạo hàm $v'\left( t \right)$ biểu thị tốc độ thay đổi của vận tốc theo thời gian, còn gọi là gia tốc của chuyển động, kí hiệu $a\left( t \right)$. Tính gia tốc của chuyển động tại thời điểm $t = 2$.

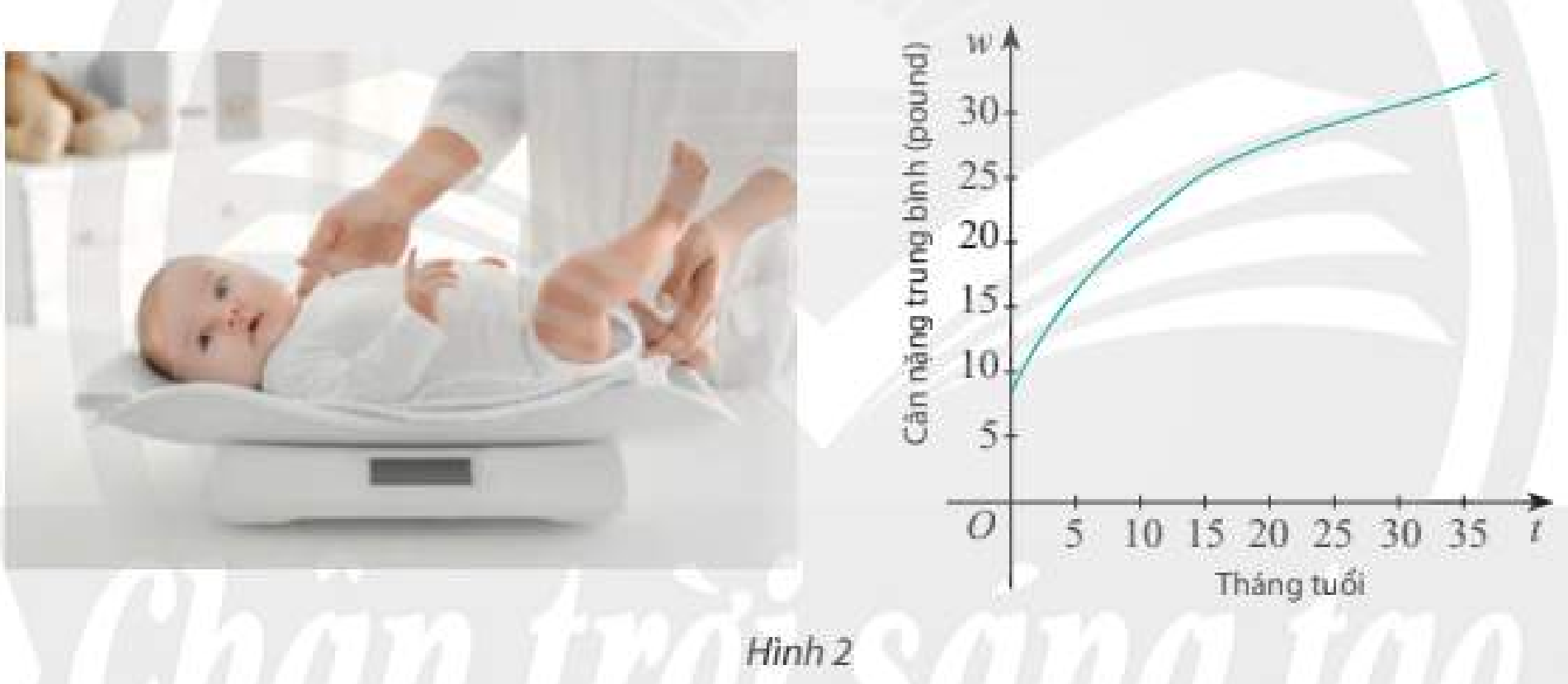
Cân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số $w\left( t \right) = 0,000758{t^3} - 0,0596{t^2} + 1,82t + 8,15$, trong đó $t$ được tính bằng tháng và $w$ được tính bằng pound (nguồn: https://www.cdc.gov/growthcharts/data/who/GrChrt_Boys). Tính tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi.

Một công ty xác định rằng tổng chi phí của họ, tính theo nghìn đô-la, để sản xuất $x$ mặt hàng là $C\left( x \right) = \sqrt {5{x^2} + 60}$ và công ty lên kế hoạch nâng sản lượng trong $t$ tháng kể từ nay theo hàm số $x\left( t \right) = 20t + 40$. Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó?

Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức $s\left( t \right) = 0,81{t^2}$, trong đó $t$ là thời gian được tính bằng giây và ${\rm{s}}$ tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm $t = 2$ sau khi thả vật đó, tính:

a) Quãng đường vật đã rơi;

b) Gia tốc của vật.

Tính đạo hàm của hàm số $y =  - {x^2} + 2x + 1$ tại điểm ${x_0} =  - 1.$

Cho hàm số $f(x) = {x^2} + {\sin ^3}x$. Khi đó $f'\left( {\frac{\pi }{2}} \right)$ bằng

A. $\pi$.                                

B. $2\pi$.                    

C. $\pi  + 3$.                

D. $\pi  - 3$.

Tính đạo hàm của hàm số $f\left( x \right)= \log x$ tại điểm ${x_0} = \frac{1}{2}$.

Tính đạo hàm của hàm số $f\left( x \right) = {10^x}$ tại điểm ${x_0} =  - 1$.

Tính đạo hàm của hàm số $f\left( x \right) = \cot x$ tại điểm ${x_0} =  - \frac{\pi }{3}$.

Tính đạo hàm của hàm số $f\left( x \right) = \tan x$ tại điểm ${x_0} =  - \frac{\pi }{6}$.

Một vật dao động theo phương trình f(x) = cosx, trong đó x là thời gian tính theo giây. Tính vận tốc tức thời của vật tại thời điểm ${x_0} = 2\left( s \right)$.

Tính đạo hàm của hàm số f(x) = sinx tại điểm ${x_0} = \frac{\pi }{2}$.

Tính đạo hàm của hàm số $f\left( x \right) = \sqrt x$ tại điểm ${x_0} = 9$.

Cho hàm số $y = {x^{22}}$.

a) Tính đạo hàm của hàm số trên tại điểm x bất kì.

b) Tính đạo hàm của hàm số trên tại điểm ${x_0} =  - 1$.

Một vật rơi tự do theo phương thẳng đứng có phương trình $s = \frac{1}{2}g{t^2}$, trong đó g là gia tốc rơi tự do, $g \approx 9,8m/{s^2}$.

a) Tính vận tốc tức thời v(t) tại thời điểm ${t_0} = 4(s);{t_1} = 4,1(s)$.

b) Tính tỉ số $\frac{{\Delta v}}{{\Delta t}}$ trong khoảng thời gian $\Delta t = {t_1} - {t_0}$.

Hàm số $y = {x^3} - 3x + 1$ có đạo hàm tại $x =  - 1$ bằng

A. 0

B. 6

C. $- 6$

D. $- 1$

Vận tốc tức thời của chuyển động $s = f\left( t \right)$ tại thời điểm ${t_0}$ là:

A. $f'\left( {{t_0}} \right).$

B. $f\left( {{t_0}} \right) - f'\left( {{t_0}} \right).$

C. $f\left( {{t_0}} \right).$

D. $- f'\left( {{t_0}} \right).$

Chứng minh rằng hàm số $f\left( x \right) = \left| {x - 2} \right|$ không có đạo hàm tại điểm ${x_0} = 2,$ nhưng có đạo hàm tại mọi điểm $x \ne 2.$

Một chất điểm chuyển động theo phương trình $s\left( t \right) = \frac{1}{3}{t^3} - 3{t^2} + 8t + 2,$trong đó $t > 0,{\rm{ }}t$ tính bằng giây, $s\left( t \right)$ tính bằng mét. Tính vận tốc tức thời của chất điểm tại thời điểm t = 5 (s).

Một mạch dao động điện từ LC có lượng điện tích dịch chuyển qua tiết diện thẳng của dây xác định bởi hàm số $Q\left( t \right) = {10^{ - 5}}sin\left( {2000t + \frac{\pi }{3}} \right),$trong đó $t > 0,{\rm{ }}t$ tính bằng giây, Q tính bằng Coulomb. Tính cường độ dòng điện tức thời I (A) trong mạch tại thời điểm $t = \frac{\pi }{{1500}}\left( s \right)$, biết $I\left( t \right){\rm{ }} = {\rm{ }}Q'\left( t \right).$