Nội dung từ Loigiaihay.Com
Kết quả của phép tính \({\left( {\frac{{ - 1}}{2}} \right)^3}\) là:
-
A.
\(\frac{{ - 1}}{6}\).
-
B.
\( - \frac{1}{8}\).
-
C.
\(\frac{{ - 1}}{{ - 8}}\).
-
D.
\(\frac{1}{8}\).
Sử dụng kiến thức về lũy thừa \({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\).
Ta có: \({\left( {\frac{{ - 1}}{2}} \right)^3} = \frac{{{{\left( { - 1} \right)}^3}}}{{{2^3}}} = - \frac{1}{8}\)
Đáp án B.
Đáp án : B

Các bài tập cùng chuyên đề
Viết các tích sau dưới dạng lũy thừa rồi chỉ ra cơ số và số mũ của lũy thừa đó.
a) 2.2.2.2; b) 5.5.5
Thực hiện phép tính:
a) (-2).(-2).(-2)
b) (-0,5).(-0,5);
c) \(\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\)
Hãy viết các biểu thức trong HĐ 2 dưới dạng lũy thừa tương tự như lũy thừa của số tự nhiên
Tính:
\(\begin{array}{l}a){\left( { - \frac{4}{5}} \right)^4}\\b){(0,7)^3}\end{array}\)
Tính:
\(\begin{array}{l}a){\left( {\frac{2}{3}} \right)^{10}}{.3^{10}}\\b){( - 125)^3}{:25^3}\\c){(0,08)^3}{.10^6}\end{array}\)
Viết công thức tính thể tích của hình lập phương cạnh a dưới dạng lũy thừa. Từ đó viết biểu thức lũy thừa đẻ tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilomét khối).
Bài toán mở đầu:
Trái Đất, ngôi nhà chung của tất cả chúng ta có khoảng 71% diện tích bề mặt được bao phủ bởi nước. Nếu gom hết toàn bộ lượng nước trên Trái Đất để đổ đầy vào một bể chứa hình lập phương thì kích thước cạnh của bể lên tới 1 111,34 km.(Theo usgs.gov)
Muốn biết lượng nước trên Trái Đất là khoảng bao nhiêu kilomet khối, ta cần tính 1 111,34. 1 111,34. 1 111,34. Biểu thức này có thể viết gọn hơn dưới dạng lũy thừa giống như lũy thừa của một số tự nhiên em đã học ở lớp 6.
Viết các số 125; 3 125 dưới dạng lũy thừa của 5.
Viết các số \({\left( {\frac{1}{9}} \right)^5};{\left( {\frac{1}{{27}}} \right)^7}\) dưới dạng lũy thừa cơ số \(\frac{1}{3}\).
Tính:
\({\left( {\frac{{ - 2}}{3}} \right)^3};{\left( {\frac{{ - 3}}{5}} \right)^2};{\left( { - 0,5} \right)^3}; {\left( { - 0,5} \right)^2};\,{\left( {37,57} \right)^0};\,{\left( {3,57} \right)^1}\).
Viết các số sau dưới dạng luỹ thừa với số mũ lớn hơn 1:
\(0,49;\,\frac{1}{{32}};\,\frac{{ - 8}}{{125}};\,\frac{{16}}{{81}};\,\frac{{121}}{{169}}\)
a)Tính: \({\left( {\frac{{ - 1}}{2}} \right)^5};{\left( {\frac{{ - 2}}{3}} \right)^4};{\left( { - 2\frac{1}{4}} \right)^3};{\left( { - 0,3} \right)^5};{\left( { - 25,7} \right)^0}\).
b)Tính: \({\left( { - \frac{1}{3}} \right)^2};{\left( { - \frac{1}{3}} \right)^3};{\left( { - \frac{1}{3}} \right)^4};{\left( { - \frac{1}{3}} \right)^5}\).
Hãy rút ra nhận xét về dấu của luỹ thừa với số mũ chẵn và luỹ thừa với số mũ lẻ của một số hữu tỉ âm.
Viết các tích sau dưới dạng lũy thừa và nêu cơ số, số mũ của chúng:
a)\(7.7.7.7.7\) b) 12.12…12 ( n thừa số 12)\(\left( {n \in \mathbb{N},n > 1} \right)\)
Tính thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8m.
Tính: \({\left( {\frac{{ - 3}}{4}} \right)^3};{\left( {\frac{1}{2}} \right)^5}\)
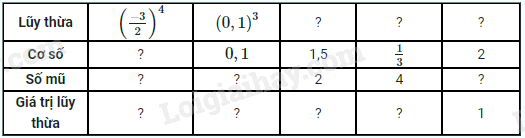
Tìm số thích hợp cho “?” trong bảng sau:
Trên bản đồ có tỉ lệ 1: 100 000, một cánh đồng lúa có dạng hình vuông với độ dài cạnh là \(0,7\;{\rm{cm}}\). Tính diện tích thực tế theo đơn vị mét vuông của cánh đồng lúa đó (viết kết quả dưới dạng \(a{.10^n}\) với \(1 \le a < 10\) )
Hai mảnh vườn có dạng hình vuông. Mảnh vườn thứ nhất có độ dài cạnh là 19,5 m. Mảnh vườn thứ hai có độ dài cạnh là 6,5 m. Diện tích mảnh vườn thứ nhất gấp bao nhiều lần diện tích mảnh vườn thứ hai?
Sắp xếp các số sau theo thứ tự tăng dần:
a) \({(0,2)^0};{(0,2)^3};{(0,2)^1};{(0,2)^2};\)
b) \({( - 1,1)^2};{( - 1,1)^0};{( - 1,1)^1};{( - 1,1)^3}\).
Tính \(\left(\frac{2}{3}\right)^3\) bằng
Đơn vị đo thời gian nhỏ nhất là yoctosecond (viết tắt là ys), nó bằng 0,000000000000000000000001 giây. Hãy viết số này dưới dạng luỹ thừa của một số hữu tỉ.
Đường kính của một tế bào hồng cầu là khoảng \(7,4.{\left( {\dfrac{1}{{10}}} \right)^4}\)cm. Hãy viết số này dưới dạng số thập phân.
Viết các số sau dưới dạng lũy thừa với số mũ lớn hơn 1.
\(9; \dfrac{1}{8}\);\(\dfrac{{81}}{{16}}\);\(\dfrac{8}{{125}};0,0625 \)
Tính
a) \({\left( {\dfrac{{ - 1}}{3}} \right)^4}\),\({\left( {\dfrac{{ - 2}}{3}} \right)^3}\),\({\left( {2\dfrac{1}{2}} \right)^3}\),\({\left( { - 0,2} \right)^3}\)
b) \({\left( {\dfrac{{ - 1}}{2}} \right)^2}\),\({\left( {\dfrac{{ - 1}}{2}} \right)^3}\),\({\left( {\dfrac{{ - 1}}{2}} \right)^4}\),\({\left( {\dfrac{{ - 1}}{2}} \right)^5}\)
Tính:
a) \({2^5}\);
b) \({( - {\rm{ }}5)^3}\); c) \({(0,4)^3}\);
d) \({( - {\rm{ 0,4)}}^3}\);
e) \({\left( {\dfrac{1}{2}} \right)^5}\);
g) \({\left( {\dfrac{{ - 1}}{3}} \right)^4}\);
h) \({(21,5)^0}\);
i) \({\left( {3\dfrac{1}{2}} \right)^2}\).
Viết mỗi số sau dưới dạng lũy thừa với cơ số cho trước:
a) 343 với cơ số 7;
b) 0,36 với cơ số 0,6 và – 0,6;
c) \( - \dfrac{8}{{27}}\) với cơ số \( - \dfrac{2}{3}\);
d) 1,44 với cơ số 1,2 và – 1,2.
So sánh:
a) \({\left( {\dfrac{1}{2}} \right)^{40}}\) và \({\left( {\dfrac{1}{2}} \right)^{50}}\);
b) \({243^3}\) và \({125^5}\).
Giá trị của \(n\) bằng bao nhiêu nếu \({\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}.\)
A.2.
B.4.
C.1.
D.3.
Viết các số 125; 3125 dưới dạng lũy thừa của 5.
Viết các số \({\left( {\frac{1}{9}} \right)^5};{\left( {\frac{1}{{27}}} \right)^7}\) dưới dạng lũy thừa cơ số \(\frac{1}{3}\)
Thay mỗi dấu “?” bởi một lũy thừa của 3, biết rằng từ ô thứ ba, lũy thừa cần tìm là tích của hai lũy thừa ở hai ô liền trước.













