Nội dung từ Loigiaihay.Com
Cho hai biến cố A,B với 0<P(B)<1 và P(A∩B)=0,2;P(A∩¯B)=0,3. Khi đó, P(A) bằng:
A. 0,06.
B. 0,5.
C. 0,1.
D. 0,67.
Sử dụng công thức tính xác suất toàn phần: P(A)=P(A∩B)+P(A∩¯B).
Ta có: P(A)=P(A∩B)+P(A∩¯B)=0,2+0,3=0,5.
Chọn B

Các bài tập cùng chuyên đề
Với giả thiết như vận dụng trên.
a) Hãy ước lượng tỉ lệ cây con có kiểu gene BB.
b) Sử dụng kết quả của vận dụng trên và câu a, hãy ước lượng tỉ lệ cây con có kiểu gene Bb.
Trở lại Ví dụ 1. Sử dụng sơ đồ hình cây, hãy mô tả cách tính xác suất để thứ Tư, ông An đi làm bằng xe buýt.
Trở lại tình huống mở đầu Mục 1. Tính xác suất để nhà tổ chức sự kiện bán hết vé
Trong quân sự, một máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X với xác suất 0,55. Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.
Xét phương án tác chiến sau: Nếu máy bay xuất hiện tại X thì bắn 2 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn 1 quả tên lửa.
Biết rằng xác xuất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 1 quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên.
Có hai chuồng thỏ. Chuồng I có 5 con thỏ đen và 10 con thỏ trắng. Chuồng II có 7 con thỏ đen và 3 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 1 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 1 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.
Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải trải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK; nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường.
a) Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.
b) Dùng sơ đồ hình cây, hãy mô tả cách tính xác suất để linh kiện điện tử được chọn không được đóng dấu OTK.
Chuồng I có 5 con gà mái, 2 con gà trống. Chuồng II có 3 con gà mái, 5 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 3 thì bác chọn chuồng I. Nếu số chấm không chia hết cho 3 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Hãy giải bài toán mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.
Cho hai biến cố A, B với P(B)=0,6;P(A|B)=0,7 và P(A|¯B)=0,4. Khi đó, P(A) bằng
A. 0,7.
B. 0,4.
C. 0,58.
D. 0,52.
Vào mỗi buổi sáng ở tuyến phố H, xác suất xảy ra tắc đường khi trời mưa và không mưa lần lượt là 0,7 và 0,2. Xác suất có mưa vào một buổi sáng là 0,1. Tính xác suất để sáng đó tuyến phố H bị tắc đường.
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau:
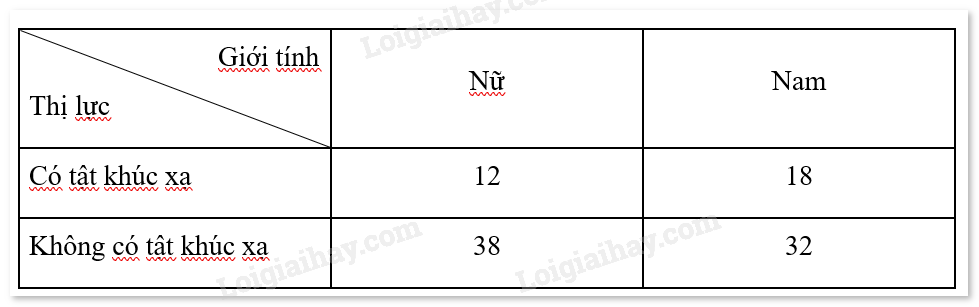
Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên.
a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam.
b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.
Trong kì thi học sinh giỏi quốc gia, tỉnh X có hai đội tuyển môn Toán và môn Ngữ văn tham dự. Đội tuyển Toán có 10 em, đội tuyển Ngữ văn có 8 em. Xác suất có giải của mỗi em trong đội tuyển Toán là 0,8; trong đội tuyển Ngữ văn là 0,7. Sau giải lấy ngẫu nhiên một em của tỉnh X trong số các em thi học sinh giỏi môn Toán và môn Ngữ văn. Tính xác suất để em đó là một em được giải.
Giải ngoại hạng Anh có 20 đội. Hiện tại đội Tottenham xếp vị trí thứ 8. Trong trận tới nếu gặp đội xếp trên thì Tottenham có xác suất thắng là 0,2; xác suất thua là 0,5. Nếu gặp đội xếp dưới thì Tottenham có xác suất thắng là 0,5 và xác suất thua là 0,3.
Bốc thăm ngẫu nhiên một đội đấu với đội Tottenham trong trận tới. Tính xác suất để đội Tottenham hòa trong trận tới.
Có hai túi kẹo. Túi I có 3 chiếc kẹo sô cô la đen và 2 chiếc kẹo sô cô la trắng. Túi II có 4 chiếc kẹo sô cô la đen và 3 chiếc kẹo sô cô la trắng. Từ túi I lấy ngẫu nhiên một chiếc kẹo. Nếu là chiếc kẹo sô cô la đen thì thêm 2 chiếc kẹo sô cô la đen vào túi II. Nếu là chiếc kẹo sô cô la trắng thì thêm hai chiếc kẹo sô cô la trắng vào túi II. Sau đó từ túi II lấy ngẫu nhiên một chiếc kẹo. Tính xác suất để lấy được chiếc kẹo sô cô la trắng.
Trong một lớp học nhạc có 60% là học sinh nữ. Biết rằng có 20% học sinh nữ học violon, 30% học sinh nam học violon. Chọn ngẫu nhiên một học sinh.
a) Tính xác suất để học sinh này là nam và chơi violon.
b) Tính xác suất để học sinh này học violon.
Nếu hai biến cố A,B thoả mãn P(B)=0,4;P(A|B)=0,5;P(A|¯B)=0,3 thì P(A) bằng:
A. 0,38.
B. 0,8.
C. 0,2.
D. 0,18.
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Một kho hàng có các thùng hàng với bề ngoài giống hệt nhau, trong đó có 24 thùng hàng loại I và 26 thùng hàng loại II. Trong số các thùng hàng đó, có 95% thùng hàng loại I và 80% thùng hàng loại II đã được kiểm định. Chọn ngẫu nhiên một thùng hàng.
Xét các biến cố:
A: “Chọn được thùng hàng loại I;
B: “Chọn được thùng hàng đã được kiểm định”.
a) P(A)=0,48;P(¯A)=0,52.
b) P(B|A)=0,8.
c) P(B|¯A)=0,95.
d) P(B)=0,872.
Trước khi đưa ra thị trường một sản phẩm, công ty phỏng vấn 800 khách hàng và được kết quả là 550 người nói sẽ mua, còn 250 người nói sẽ không mua. Theo kinh nghiệm của nhà sản xuất thì trong những người nói sẽ mua sẽ có 60% số người chắc chắn mua, còn trong những người nói sẽ không mua lại có 1% người chắc chắn mua. Chọn ngẫu nhiên một khách hàng. Xác suất chọn được khách hàng chắc chắn mua là bao nhiêu?
Huy thực hiện liên tiếp hai thí nghiệm. Thí nghiệm thứ nhất có xác suất thành công là 0,6. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,8. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai là 0,3. Tính xác suất của các biến cố
A: “Cả hai thí nghiệm đều thành công”;
B: “Thí nghiệm thứ nhất không thành công, còn thí nghiệm thứ hai thành công”;
C: “Thí nghiệm thứ hai thành công”.
Trong một ngày hội giao lưu học sinh, chỉ có 350 học sinh trường Hoà Bình và 450 học sinh trường Minh Phúc đứng ở hội trường. Trong các học sinh giao lưu, tỉ lệ học sinh trường Hoà Bình bị cận thị là 0,2, còn tỉ lệ học sinh trường Minh Phúc bị cận thị là 0,3. Các học sinh của hai trường đứng lẫn với nhau. Chọn ngẫu nhiên một học sinh. Xác suất chọn được học sinh bị cận thị là bao nhiêu?
Trên bàn có hai hộp bi với hình dạng và kích thước như nhau. Hộp thứ nhất có 6 viên bi đỏ, 7 viên bi vàng; còn hộp thứ hai có 10 viên bi đỏ, 11 viên bi vàng. Các viên bị có hình dạng và kích thước như nhau. Chọn ngẫu nhiên một hộp bi và từ hộp đó lấy ngẫu nhiên một viên bị. Tính xác suất để viên bị được lấy có màu đỏ.
Một vận động viên bóng bàn thắng 60% các séc đấu anh ta được ra bóng trước và 45% các séc đấu anh ta không được ra bóng trước. Trong một séc đấu, trọng tài gieo một đồng xu cân đối để xác định ai là người ra bóng trước. Tính xác suất vận động viên đó thắng séc đấu.
Cho P(A)=27;P(B|A)=14;P(B|¯A)=15. Giá trị của P(B) là
Có hai chuồng thỏ. Chuồng I có 6 con thỏ đen và 10 con thỏ trắng. Chuồng II có 8 con thỏ đen và 4 con thỏ trắng. Trước tiên, từ chuồng I lấy ra ngẫu nhiên một con thỏ rồi cho vào chuồng II. Sau đó, từ chuồng II lấy ra ngẫu nhiên một con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.
Ở một địa phương, tỉ lệ nam và nữ là 2:3. Số người mắc bệnh bạch tạng của địa phương này chiếm tỉ lệ 0,45% dân cư. Tính tỉ lệ nam giới mắc bệnh bạch tạng của địa phương đó, biết tỉ lệ này ở nữ là 0,35%.
Một hộp có 5 quả cầu trắng và 10 quả cầu đen cùng kích thước và khối lượng. Lấy ngẫu nhiên lần lượt hai quả cầu (không hoàn lại) từ hộp. Tính xác suất để lần thứ hai lấy được quả cầu trắng.
Cho hai biến cố A, B với P(B) = 0,8, P(A|B) = 0,7, P(A|¯B) = 0,45. Tính P(A).
Giả sử tỉ lệ người dân của tỉnh Khánh Hòa nghiện thuốc lá là 20%; tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là 70%, trong số người không nghiện thuốc lá là 15%. Hỏi khi ta gặp ngẫu nhiên một người dân của tỉnh Khánh Hòa thì khả năng mà đó bị bệnh phổi là bao nhiêu %?
Cho hai biến cố A, B, biết 0 < P(A) < 1, xác suất của biến cố B được tính theo công thức nào sau đây?












