Nội dung từ Loigiaihay.Com
Với góc nhọn \(\alpha \), ta có:
-
A.
\({\rm{cos}}\left( {90^\circ - \alpha } \right) = \cot \alpha \).
-
B.
\(\sin \left( {90^\circ - \alpha } \right) = \tan \alpha \).
-
C.
\(\sin \left( {90^\circ - \alpha } \right) = \cot \alpha \).
-
D.
\(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha \).
Dựa vào kiến thức về tỉ số lượng giác của hai góc phụ nhau.
Theo tỉ số lượng giác của hai góc phụ nhau, ta có \(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha \).
Đáp án D.
Đáp án : D

Các bài tập cùng chuyên đề
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng?
Cho tam giác $ABC$ vuông tại $A$. Hãy tính $\tan C$ biết rằng \(\cot B = 2\).
Tính giá trị biểu thức $A = {\sin ^2}1^\circ + {\sin ^2}2^\circ + ... + {\sin ^2}88^\circ + {\sin ^2}89^\circ + {\sin ^2}90^\circ $
Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $
Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì
Cho tam giác \(ABC\) vuông tại \(A\). Hãy tính \(\tan C\) biết rằng \(\tan B = 4\).
Tính giá trị biểu thức \({\sin ^2}{10^ \circ } + {\sin ^2}{20^ \circ } + \,\,\,...\,\,\, + {\sin ^2}{70^ \circ } + {\sin ^2}{80^ \circ }\)
Tính giá trị biểu thức \(B = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .....tan80^\circ \)
Giá trị của biểu thức \(P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\) bằng
Biết \({0^0} < \alpha < {90^0}\). Giá trị bủa biểu thức \(\left[ {\sin \alpha + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha - 2\cos \left( {{{90}^0} - \alpha } \right)} \right]\) bằng:
Cho tam giác ABC vuông tại C, có \(\widehat A = \alpha ,\widehat B = \beta \) (H.4.9) . Hãy viết các tỉ số lượng giác của góc \(\alpha ,\beta \) theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
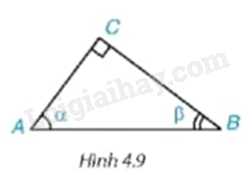
Hãy giải thích tại sao \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn \({45^0}:\)
\(\sin {55^0};\cos {62^0};\tan {57^0};\cot {64^0}\)
b) Tính \(\frac{{\tan {{25}^0}}}{{\cot {{65}^0}}},\tan {34^0} - \cot {56^0}.\)
Với mọi góc nhọn \(\alpha \) ta có
A. \(\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha \)
B. \(\tan \left( {{{90}^0} - \alpha } \right) = \cos \alpha \)
C. \(\cot \left( {{{90}^0} - \alpha } \right) = 1 - \tan \alpha \)
D. \(\cot \left( {{{90}^0} - \alpha } \right) = \sin \alpha \)
a) Tính các tỉ số lượng giác của góc \(\alpha \) và của góc 90o -\(\alpha \) trong Hình 8 theo a, b, c.
b) So sánh sin \(\widehat B\) và cos \(\widehat C\) , cos \(\widehat B\) và sin \(\widehat C\) , tan \(\widehat B\) và cot \(\widehat C\) , tan \(\widehat C\) và cot \(\widehat B\).
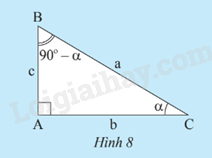
a) So sánh: sin 72o và cos 18o ; cos 72o và sin 18o; tan 72o và cot 18o
b) Cho biết sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\). Tính cos 72o và cot 72o.
Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x \( \approx 0,78\) và cot x \( \approx 1,25\). Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).
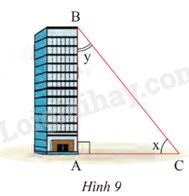
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45o:
a) sin 60o
b) cos 75o
c) tan 80o
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 7).
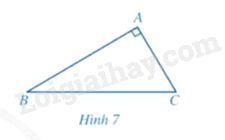
a) Tổng số đo của góc \(B\) và góc \(C\) bằng bao nhiêu?
b) Viết công thức tính các tỉ số lượng giác của góc \(B\) và góc \(C\).
c) Mỗi tỉ số lượng giác của góc \(B\) bằng tỉ số lượng giác nào của góc \(C\)?
Tính:
a) \(\sin 61^\circ - \cos 29^\circ \);
b) \(\cos 15^\circ - \sin 75^\circ \)
c) \(\tan 28^\circ - \cot 62^\circ \);
d) \(\cot 47^\circ - \tan 43^\circ \).
Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc \(63^\circ \)? Vì sao?
a) \(\sin 27^\circ \)
b) \(\cos 27^\circ \)
c) \(\tan 27^\circ \)
d) \(\cot 27^\circ \)
Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị biểu thức:
\(A = \sin 25^\circ + \cos 25^\circ - \sin 65^\circ - \cos 65^\circ \).
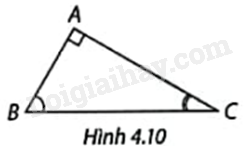
Cho tam giác ABC vuông tại A (Hình 4.10).
a) Tổng số đo của góc B và góc C bằng bao nhiêu độ?
b) Viết các tỉ số lượng giác của góc B và góc C, từ đó chỉ ra các cặp tỉ số lượng giác bằng nhau.
Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc lớn hơn \({45^o}\):
a) \(\cos {25^o}\);
b) \(\cot {31^o}\).
Cho \(\alpha = 35^\circ ;\beta = 55^\circ \). Khẳng định nào sau đây là sai?
Tính \(\sin 40^\circ - \cos 50^\circ \).
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45o.
a) cos 69o
b) cot 83o
c) sin 77o
d) tan 51o
Cho tam giác ABC có AB = \(\sqrt 2 \) cm, BC = \(\sqrt 5 \) cm, AC = \(\sqrt 3 \) cm. Tỉnh các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị mỗi biểu thức sau:
a) \(\frac{{\sin 39^\circ }}{{\cos 51^\circ }}\)
b) \(\cos 37^\circ 30' - \sin 52^\circ 30'\)
c) \(\tan 73^\circ - \cot 17^\circ \)
d) \(\cot 44^\circ .\cot 46^\circ \)
Tính giá trị của mỗi biểu thức sau:
a) \(A{\rm{ }} = {\rm{ }}si{n^2}79^\circ + {\rm{ }}co{s^2}79^\circ \)
b) \(B = \tan 73^\circ .\tan 37^\circ .\tan 53^\circ .\tan 17^\circ \)
c) \(C = {\cos ^2}73^\circ + {\cos ^2}53^\circ + {\cos ^2}17^\circ + {\cos ^2}37^\circ \)
d) \(D = \sin 59^\circ + \cos 59^\circ - \sin 31^\circ - \cos 31^\circ \)












