Nội dung từ Loigiaihay.Com
1. Giải các phương trình và bất phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
b) \(\frac{{2x + 1}}{{2x}} - \frac{x}{{x + 2}} = 0\)
c) \(3x - 5 < 2x + 2\)
d) \(\frac{{2x + 3}}{2} \ge \frac{{1 - x}}{3} + 1\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = - 3\end{array} \right.\)
1. a) Đưa phương trình về phương trình tích để giải.
b) Tìm điều kiện xác định, quy đồng mẫu và giải phương trình tìm được. Sau đó kiểm tra điều kiện của các nghiệm tìm được.
c, d) Dựa vào cách giải bất phương trình bậc nhất một ẩn và phương trình đưa về dạng bất phương tình bậc nhất một ẩn.
2. Sử dụng phương pháp cộng đại số để giải hệ phương trình.
1. Giải các phương trình và bất phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
\(\begin{array}{l}{x^2} - x + 3x - 3 = 0\\\left( {{x^2} - x} \right) + \left( {3x - 3} \right) = 0\\x\left( {x - 1} \right) + 3\left( {x - 1} \right) = 0\\\left( {x + 3} \right)\left( {x - 1} \right) = 0\end{array}\)
+) \(x + 3 = 0\) suy ra \(x = - 3\).
+) \(x - 1 = 0\) suy ra \(x = 1\).
Vậy phương trình có hai nghiệm \(x = - 3;x = 1\).
b) \(\frac{{2x + 1}}{{2x}} - \frac{x}{{x + 2}} = 0\)
ĐKXĐ: \(2x \ne 0\) và \(x + 2 \ne 0\)
hay \(x \ne 0\) và \(x \ne - 2\).
Ta có: \(\frac{{2x + 1}}{{2x}} - \frac{x}{{x + 2}} = 0\)
\(\begin{array}{l}\frac{{\left( {2x + 1} \right)\left( {x + 2} \right)}}{{2x\left( {x + 2} \right)}} - \frac{{x.2x}}{{2x\left( {x + 2} \right)}} = 0\\\left( {2x + 1} \right)\left( {x + 2} \right) - x.2x = 0\\2{x^2} + x + 4x + 2 - 2{x^2} = 0\\5x + 2 = 0\\x = \frac{{ - 2}}{5}\left( {TM} \right)\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{ - 2}}{5}\).
c) \(3x - 5 < 2x + 2\)
\(\begin{array}{l}3x - 2x < 2 + 5\\x < 7\end{array}\)
Vậy nghiệm của bất phương trình là \(x < 7\).
d) \(\frac{{2x + 3}}{2} \ge \frac{{1 - x}}{3} + 1\)
\(\begin{array}{l}\frac{{3\left( {2x + 3} \right)}}{{2.3}} \ge \frac{{2\left( {1 - x} \right)}}{{3.2}} + \frac{6}{6}\\3\left( {2x + 3} \right) \ge 2\left( {1 - x} \right) + 6\\6x + 9 \ge 2 - 2x + 6\\6x + 2x \ge 2 + 6 - 9\\8x \ge - 1\\x \ge \frac{{ - 1}}{8}\end{array}\)
Vậy nghiệm của bất phương trình là \(x \ge \frac{{ - 1}}{8}\).
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = - 3\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = - 3\end{array} \right.\)
Nhân cả hai vế của phương trình \(2x - y = 4\) với 2, ta được hệ phương trình \(\left\{ \begin{array}{l}4x - 2y = 8\\x + 2y = - 3\end{array} \right.\).
Cộng hai vế của hai phương trình trong hệ mới, ta được \(5x = 5\) suy ra \(x = 1\).
Thế vào phương trình \(2x - y = 4\), ta được \(2.1 - y = 4\) suy ra \(y = - 2\).
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {1; - 2} \right)\).

Các bài tập cùng chuyên đề
Một hãng viễn thông nước ngoài có hai gói cước như sau:
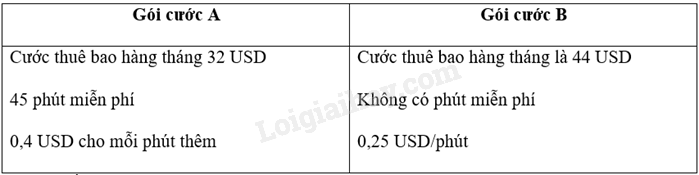
a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó.
b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào?
Không sử dụng máy tính cầm tay, hãy đưa ra hai cách khác nhau để trả lời câu hỏi dưới đây: “Bất phương trình \(2x - 3 < 5x + 3\) nhận số nào trong các số sau làm nghiệm: \( - 3; - 2,55; - \frac{1}{7};\frac{2}{3};1,2\)?”. Trong hai cách đó, cách nào đòi hỏi ít tính toán hơn?
Chọn hãng xe nào?
Nhà máy dự định tổ chức một chuyến du lịch cho 35 công nhân được bình chọn là lao động xuất sắc. Anh Tùng được giao nhiệm vụ tìm hiểu chi phí thuê xe ô tô chở công nhân đi du lịch. Dưới đây là giá thuê xe do hai hàng xe đưa ra:
- Hãng A: Tiền thuê ban đầu là 2 triệu đồng, sau đó mỗi km của hành trình tính 8 nghìn đồng.
- Hãng B: Tiền thuê ban đầu là 1,5 triệu đồng, sau đó mỗi km của hành trình tính 9 nghìn đồng.
a) Lập bất phương trình diễn đạt giả định: “Tiền thuê xe của hãng A ít hơn tiền thuê xe của hãng B”.
b) Giải bất phương trình đó.
c) Nếu hành trình du lịch dự định của nhà máy dài 320km thì anh Tùng chọn hãng nào sẽ có lợi hơn về khoản phí thuê xe phải trả?
Số đo tính theo độ của ba góc A, B, C trong tứ giác ABCD lần lượt là x, 2x, 3(x - 10) với x > 10.
a) Viết một bất phương trình bậc nhất ẩn x.
b) Giải bất phương trình bậc nhất một ấn ở câu a.
c) Các góc có số đo là 2x và 3(x − 10) có bằng nhau được hay không? Vì sao?
Mức lương tối thiểu theo quy định ở Pháp năm 2022 là 10,25€ cho mỗi giờ làm việc.
Trong dịp hè, Laurent David làm thêm tại một khách sạn theo mức lương tối thiểu như quy định và anh ấy muốn kiếm được ít nhất 1500€ trong mùa hè này.
a) Hãy viết một bất phương trình mô tả tình huống này.
b) Hỏi anh ấy cần làm việc ít nhất bao nhiêu giờ để kiếm được số tiền trên? (€ là viết tắt của Euro, là loại tiền tệ mà 20 nước thuộc liên minh Châu Âu đang sử dụng chung)
Giải các phương trình và bất phương trình sau:
a) \(\left( {x - 1} \right)\left( {3x - 6} \right) = 0\)
b) \(\frac{2}{{x + 3}} - \frac{1}{{x - 2}} = \frac{{2x - 13}}{{\left( {x + 3} \right)\left( {x - 2} \right)}}\)
c) \(2x - 4 > 0\)
d) \(2 - 3x \le 4x + 5\)
1. Giải các phương trình và bất phương trình sau:
a) \({x^2} - 5x + 4\left( {x - 5} \right) = 0\)
b) \(\frac{x}{{x - 3}} = \frac{x}{{x + 3}} + \frac{{36}}{{{x^2} - 9}}\)
c) \(3x - 2 > 4\)
d) \(\frac{{3x - 1}}{4} + 5 \le \frac{{x - 1}}{2}\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x + y = 8\\x - y = - 5\end{array} \right.\)












