Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) là?

Giao điểm của hai đường tiệm cận của đồ thị hàm số nào dưới đây nằm trên đường thẳng $d:y = x$?

Giá trị của tham số $m$ để đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{2x + 1}}{{x + m}}$ đi qua điểm $M\left( {2;3} \right)$ là

Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\).

Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}\).

Hình 1.26 là đồ thị của hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)

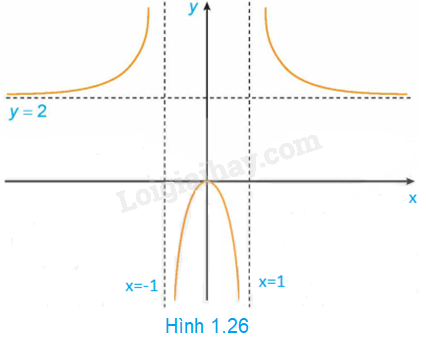
Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Tìm các tiệm cận của đồ thị hàm số sau:
a) \(y = \frac{{3 - x}}{{2x + 1}}\);
b) \(y = \frac{{2{x^2} + x - 1}}{{x + 2}}\).

Một mảnh vườn hình chữ nhật có diện tích bằng \(144{m^2}\). Biết độ dài một cạnh của mảnh vườn là x (m).

a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.

b) Tìm các tiệm cận của đồ thị hàm số P(x).

Cho hàm số \(y = f\left( x \right)\) thỏa mãn: \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = 2\) và \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 2\). Khẳng định nào sau đây là đúng?

A. Đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số.

B. Đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số.

C. Đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số.

D. Đường thẳng \(x = 2\) là tiệm cận ngang của đồ thị hàm số.

Cho hàm số \(y = f\left( x \right)\) xác định trên \[\mathbb{R}\backslash \left\{ {1;3} \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào sau đây là sai?
A. Đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng \(y = - 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
C. Đường thẳng \(x = 3\) là tiệm cận đứng của đồ thị hàm số đã cho.
D. Đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số đã cho.

Đồ thị trong Hình 1.37 là đồ thị của hàm số:

A. \(y = \frac{{x + 2}}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{x - 1}}{{x + 1}}\).
D. \(y = \frac{{x + 3}}{{1 - x}}\).

Đồ thị trong Hình 1.38 là đồ thị của hàm số:

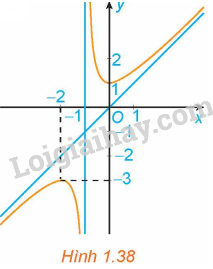
A. \(y = x - \frac{1}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\).
D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).

Tìm các tiệm cận của mỗi đồ thị hàm số sau:
a) \(y = \frac{{3x - 2}}{{x + 1}}\);
b) \(y = \frac{{{x^2} + 2x - 1}}{{2x - 1}}\).

Tổng số các đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt {{x^2} - 1} }}{x}\) là

A. 0.

B. 1.

C. 2.

D. 3.

Tìm tiệm cận đứng, ngang, xiên (nếu có) của đồ thị mỗi hàm số sau:

a) \(y = \frac{x}{{2 - x}}\)                 

b) \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)             

c) \(y = x - 3 + \frac{1}{{{x^2}}}\)

Số đường TCĐ và TCN của hàm số \(y = \frac{{4x + 4}}{{{x^2} + 2x + 1}}\) là:

A. 0. 

B.1.

C. 2. 

D. 3.

Tìm các đường TCN và TCĐ của mỗi hàm số sau:

A. \(y = \frac{{5x + 1}}{{3x - 2}}\)            

B. \(y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}}\)                          

C. \(y = \frac{x}{{\sqrt {{x^2} - 4} }}\)

Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau:

\(a,\;y = x - 3 + \frac{1}{{{x^2}}}\)

\(b,\;y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)

\(\;c,y = \frac{{2{x^2} - x + 3}}{{2x + 1}}\)

Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C(x) = \frac{{50x + 2000}}{x}\)

Tìm các đường tiệm cận của hàm số C(x).

Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau:

a) \(y = \frac{{4x - 5}}{{2x - 3}}\)

b) \(y = \frac{{ - 2x + 7}}{{4x - 3}}\) 

c) \(y = \frac{{5x}}{{3x - 7}}\)

Tìm các tiệm cận của đồ thị hàm số sau:

a) \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\)     

b) \(y = \frac{{{x^2} + x - 1}}{x}\)

c) \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)

Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:

a) \(y = \frac{{{x^2} + 2}}{{2x - 3}}\)

b) \(y = \frac{{2{x^2} - 3x - 6}}{{x + 2}}\) 

c) \(y = \frac{{2{x^2} + 9x + 11}}{{2x + 5}}\)

Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) trong Khởi động: Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)trong đó \({m_0}\) là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng.

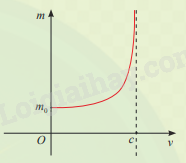
(Theo: https://www.britannica.com/science/relativistic-mass)

Cho hàm số f(x) có đồ thị như hình dưới đây:

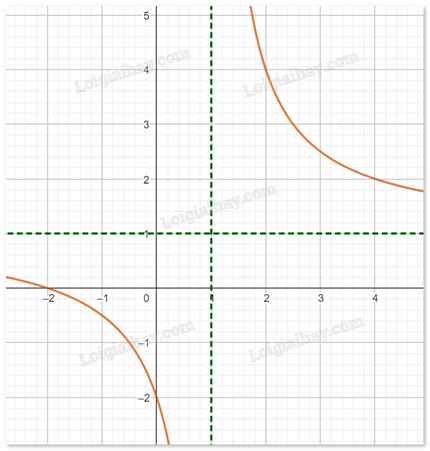
Phát biểu nào sau đây đúng?

Cho hàm số f(x) có đồ thị như hình dưới đây:

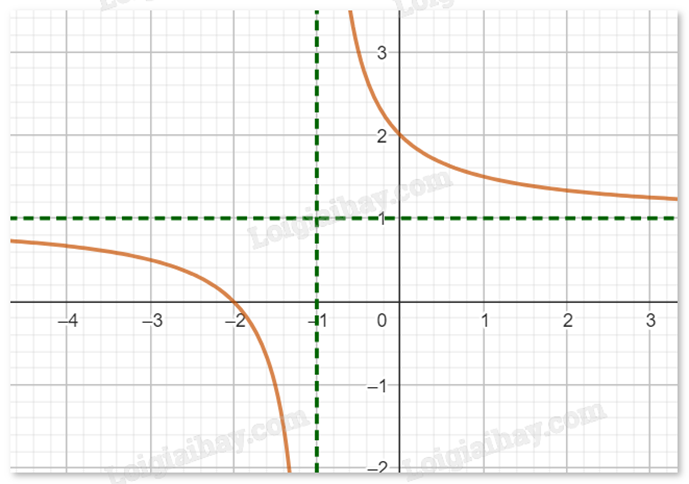
Tâm đối xứng của đồ thị hàm số có tọa độ là:

Đồ thị hàm số dưới đây có bao nhiêu đường tiệm cận?

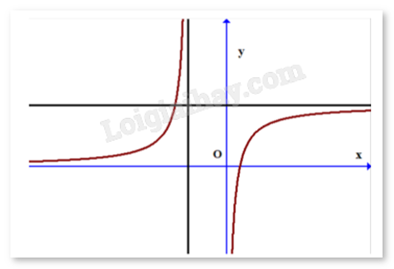
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là:

Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{x + 4}}{{x - 3}}\) là:

Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) là:

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

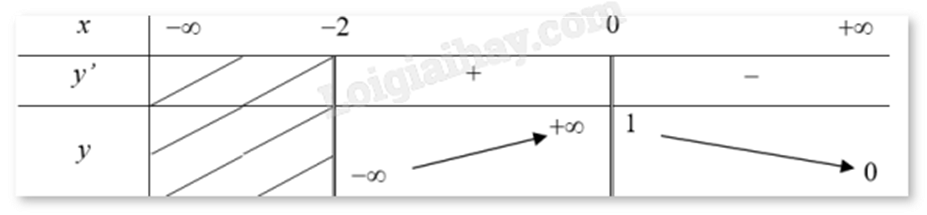
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) là: