Cho hình bình hành ABCD có \(\widehat A = 120^\circ .\) Khi đó:

A. \(\widehat B = 120^\circ ,\widehat C = 60^\circ ,\widehat D = 120^\circ .\)

B. AB // DC, AB = BC.

C. \(\widehat B = 60^\circ ,\widehat C = 120^\circ ,\widehat D = 60^\circ .\)

D. \(\widehat B = \widehat D = 60^\circ ,\widehat C = 60^\circ .\)

Bài 1 :

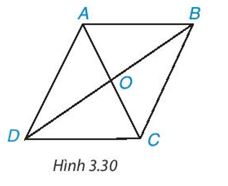
Cho hình bình hành ABCD (H.3.30).

a) Chứng minh ∆ABC = ∆CDA.

Từ đó suy ra AB = CD, AD = BC và \(\widehat {ABC} = \widehat {C{\rm{D}}A}\)

b) Chứng minh ∆ABD = ∆CDB. Từ đó suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\)

c) Gọi giao điểm của hai đường chéo AC, BD là O. Chứng minh ∆AOB = ∆COD. Từ đó suy ra OA = OC, OB = OD.

Bài 2 :

Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn thẳng AM.

Bài 3 :

Tròn khẳng định: Hình thang cân có hai cạnh bên bằng nhau. Ngược lại, hình thang có hai cạnh bên bằng nhau thì nó là hình thang cân.

Vuông lại cho rằng: Tròn sai rồi!

Có trường hợp hình thang có hai cạnh bên bằng nhau nhưng nó lại là hình bình hành mà không phải là hình thang cân.

Theo em, bạn nào đúng? Vì sao?

Bài 4 :

Hãy nêu các tính chất của hình bình hành mà em đã biết.

Bài 5 :

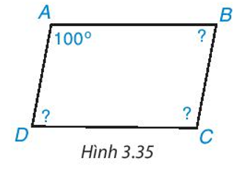
Tính các góc còn lại của hình bình hành ABCD trong Hình 3.35.

Bài 6 :

Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Chứng minh BF = DE.

Bài 7 :

Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:

a) AN = CM;

b) \(\widehat {AMC} = \widehat {ANC}\)

Bài 8 :

Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.

a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

b) Tính khoảng cách từ giao điểm đó đến điểm C.

Bài 9 :

Một khung tre hình chữ nhật có lắp đinh vít tại bốn đỉnh. Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình gì? Tại sao? Hỏi khi nẹp thêm một đường chéo vào khung đó thì nó còn bị xô lệch không?

Bài 10 :

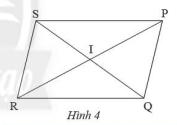
Cho hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.

Bài 11 :

Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4cm và 5cm. Tìm độ dài hai cạnh còn lại.

Bài 12 :

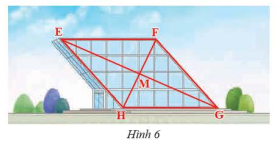
Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành \(EFGH\) với \(M\) là giao điểm của hai đường chéo (Hình 6). Cho biết \(EF = 40\)m, \(EM = 36\)m, \(HM = 16\)m. Tính độ dài cạnh \(HG\) và độ dài hai đường chéo.

Bài 13 :

Quan sát Hình 10, cho biết \(ABCD\) và \(AKCD\) đều là hình bình hành. Chứng minh ba đoạn thẳng \(AC\), \(BD\) và \(HK\) có cùng trung điểm \(O\).

Bài 14 :

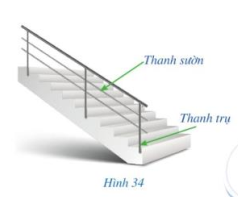
Trong thiết kế tay vịn cầu thang (Hình 34), người ta thường để các cặp thanh sườn song song với nhau, các cặp thanh trụ song song với nhau, tạo nên các hình bình hành?

Hình bình hành có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình bình hành.

Bài 15 :

Cho hình bình hành ABCD (Hình 37).

a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.

b) So sánh các cặp góc: \(\widehat {DAB}\) và \(\widehat {BCD}\); \(\widehat {ABC}\) và \(\widehat {CDA}\).

c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.

Bài 16 :

Cho hình bình hành ABCD có \(\widehat A = {80^o};AB = 4cm;BC = 5cm\). Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.

Bài 17 :

Cho hai hình bình hành ABCD và ABMN (Hình 42). Chứng minh:

a) CD = MN

b) \(\widehat {BC{\rm{D}}} + \widehat {BMN} = \widehat {DAN}\)

Bài 18 :

Cho hình bình hành MNPQ có các góc khác 90^o, MP cắt NQ tại I. Khi đó:

A. IM = IN

B. IM = IP

C. IM = IQ

D. IM = MP

Bài 19 :

Cắt hình bình hành ABCD theo đường chéo AC và xếp chồng tam giác CDA lên tam giác ABC như nhình 3.28. Em hãy nhận xét về cạnh và góc của hai tam giác.

Sử dụng tính chất của hai đường thẳng song song, em hãy cho biết vì sao \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\), từ đó giải thích vì sao \(\Delta ABC = \Delta CDA?\) Em có kết luận gì về độ dài các cặp cạnh \(AB\)  và \(CD,\)\(BC\)và \(AD\), số đo cặp góc \(\widehat B\) và \(\widehat D?\)

Bài 20 :

Cắt hình bình hành ABCD theo đường chéo AC, BD và xếp chồng tam giác OAD lên tam giác OCB như Hình 3.29. Em có nhận xét gì về cạnh và góc của hai tam giác?

Bài 21 :

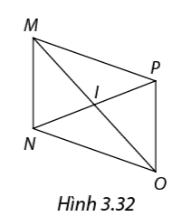
Trong hình 3.32, MONP là hình bình hành có MO và NP cắt nhau tại I và \(IN = 3cm,IO = 4cm,ON = 6cm.\) Tìm độ dài cạnh MP và đường chéo MO, NP.

Bài 22 :

Hình bình hành ABCD có \(\widehat A = 35^\circ \). Tính số đo các góc còn lại của hình bình hành đó.

Bài 23 :

Hãy chọn câu sai.

A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.

B. Hình bình hành có hai góc đối bằng nhau.

C. Hình bình hành có các cạnh đối song song và bằng nhau.

D. Hình bình hành có hai đường chéo vuông góc với nhau.

Bài 24 :

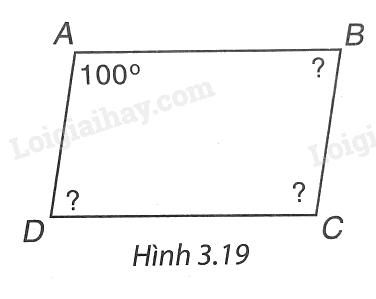
Tính các góc còn lại của hình bình hành ABCD trong Hình 3.19.

Bài 25 :

Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.

Bài 26 :

Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho \(AM = CN\). Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.

Bài 27 :

Cho hình bình hành ABCD. Vẽ hình bình hành AECF \(\left( {E \in AB,F \in CD} \right)\). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.

Bài 28 :

Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.

a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

b) Tính khoảng cách từ giao điểm đó đến điểm C.

Bài 29 :

Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều.

(Gợi ý: Chứng minh các tam giác AEF, DCF, BEC bằng nhau)

Bài 30 :

Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho \(AE = CF\); lấy các điểm G thuộc BC, H thuộc AD sao cho \(BG = DH.\) Chứng minh EGFH là một hình bình hành và các đường thẳng AC, BD, EF, GH đồng quy.