Tính giá trị biểu thức \(P = {\left( {\sqrt {20}  + 2\sqrt {45}  - 3\sqrt {80} } \right)^2}\).

Bài 1 :

Tính và so sánh \(\sqrt {{{\left( { - 3} \right)}^2}.25} \) với \(\left| { - 3} \right|.\sqrt {25} \)

Bài 2 :

Đưa thừa số ra ngoài dấu căn:

a) \(\sqrt {12} ;\)

b) \(3\sqrt {27} ;\)

c) \(5\sqrt {48} .\)

Bài 3 :

Khử mẫu của biểu thức lấy căn \(\sqrt {\frac{3}{5}} .\)

Bài 4 :

Vuông làm: \(\sqrt {{{\left( { - 2} \right)}^2}.5}  =  - 2\sqrt 5 \)

Em có đồng ý với cách làm của Vuông không? Vì sao?

Bài 5 :

Đưa thừa số ra ngoài dấu căn:

a) \(\sqrt {75} ;\)

b) \(\sqrt {27a} \left( {a \ge 0} \right);\)

c) \(\sqrt {50\sqrt 2  + 100} ;\)

d) \(\sqrt {9\sqrt 5  - 18} .\)

Bài 6 :

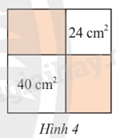
Từ một tấm thép hình vuông, người thợ cắt hai mảnh hình vuông có diện tích lần lượt là 24 cm² và 40 cm² như Hình 4. Tính diện tích phần còn lại của tấm thép.

Bài 7 :

So sánh:

a. \(\sqrt {{3^2}.11} \) và \(3\sqrt {11} \)

b. \(\sqrt {{{\left( { - 5} \right)}^2}.2} \) và \( - \left( { - 5\sqrt 2 } \right)\)

Bài 8 :

Rút gọn biểu thức: \(\sqrt 3  + \sqrt {12}  - \sqrt {27} \).

Bài 9 :

Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai, hãy rút gọn biểu thức:

a. \(\sqrt {12}  - \sqrt {27}  + \sqrt {75} \);

b. \(2\sqrt {80}  - 2\sqrt 5  - 3\sqrt {20} \);

c. \(\sqrt {2,8} .\sqrt {0,7} \).

Bài 10 :

Giải thích vì sao:

a) \(\sqrt {{3^2}.5}  = 3\sqrt 5 \)                                     

b) \(\sqrt {{{( - 2)}^2}.7}  = 2\sqrt 7 \)

Bài 11 :

Rút gọn biểu thức: \(\frac{{\sqrt {48}  + \sqrt {20} }}{{\sqrt {12}  + \sqrt 5 }}\).

Bài 12 :

Sắp xếp các số \(5\sqrt 8 ,6\sqrt 7 \) và \(3\sqrt {22} \) theo thứ tự từ nhỏ đến lớn.

Bài 13 :

Viết các số dưới dấu căn thành dạng tích rồi đưa thừa số ra ngoài dấu căn:

a) \(\sqrt {72} \).

b) \(\sqrt {147} \)

c) \(\sqrt {30000} \)

Bài 14 :

Rút gọn:

a)\(6\sqrt {50}  - \sqrt {80}  + 2\sqrt 5 \)

b) \(\frac{{\sqrt {12}  - \sqrt {112} }}{{\sqrt 3  - \sqrt {28} }}\).

Bài 15 :

Khẳng định nào sau đây là đúng?

Bài 16 :

Tính \(\sqrt {{5^2}}  + \sqrt {{{\left( { - 5} \right)}^2}} \)

Bài 17 :

Thực hiện phép tính: \(7\sqrt {12}  + 2\sqrt {27}  - 4\sqrt {75} \)

Bài 18 :

Thực hiện phép tính: \(\sqrt 5 \left( {\sqrt {20}  - 3} \right) + \sqrt {45} \)

Bài 19 :

Thực hiện phép tính: \(\left( {2 + \sqrt 3 } \right)\sqrt {7 - 4\sqrt 3 } \)

Bài 20 :

Rút gọn biểu thức bằng cách đưa thừa số ra ngoài dấu căn.

a) \(\sqrt {{{3.8}^2}} \)

b) \(\sqrt {150} \)

c) \(\sqrt {1000} \)

d) \(\sqrt {{2^2}{{.5}^4}.7} \)

Bài 21 :

Rút gọn biểu thức \(\sqrt {245}  - \sqrt {75}  + \sqrt {45}  - \sqrt {12} \) nhận được biểu thức có dạng \(a\sqrt 5  + b\sqrt 3 \). Giá trị của a – b là

A. 17

B. 3

C. 9

D. 10

Bài 22 :

Đưa thừa số ra ngoài dấu căn:

a) \(\sqrt {52} \);

b) \(\sqrt {27a} \left( {a \ge 0} \right)\);

c) \(\sqrt {50\sqrt 2  + 100} \);

d) \(\sqrt {9\sqrt 5  - 18} \).

Bài 23 :

Bài 24 :

Bài 25 :