Nội dung từ Loigiaihay.Com
lim bằng:
A. 1.
B. 0.
C. 3.
D. 2.
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng quy tắc tính giới hạn của thương để tính giới hạn.
\lim \frac{{n + 3}}{{{n^2}}} = \lim \frac{{{n^2}\left( {\frac{1}{n} + \frac{3}{{{n^2}}}} \right)}}{{{n^2}}} = \lim \left( {\frac{1}{n} + \frac{3}{{{n^2}}}} \right) = 0
Chọn B.

Các bài tập cùng chuyên đề
Kết quả của giới hạn \lim \left( {\frac{1}{{1.4}} + \frac{1}{{2.5}} + ... + \frac{1}{{n\left( {n + 3} \right)}}} \right) là:
Một quả bóng cao su được thả từ độ cao 5 m xuống một mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng \frac{2}{3} độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử {u_n} là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ n. Chứng minh rằng dãy số \left( {{u_n}} \right) có giới hạn là 0.
Cho dãy số \left( {{u_n}} \right) với {u_n} = \frac{{{{3.2}^n} - 1}}{{{2^n}}}. Chứng minh rằng \mathop {lim}\limits_{n \to + \infty } {u_n} = 3.
Cho dãy số \left( {{u_n}} \right) với {u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}. Xét dãy số \left( {{v_n}} \right) xác định bởi {v_n} = {u_n} - 1. Tính \mathop {lim}\limits_{n \to + \infty }{v_n}\;.
Chứng minh rằng: \mathop {lim}\limits_{n \to + \infty } \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}}\; = 0.
Cho dãy số \left( {{u_n}} \right) với {u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ {u_n} đến 0 nhỏ hơn 0,01?
Cho hàm số f(x) = \left\{ \begin{array}{l} - x,x < 0\\\sqrt x ,x \ge 0\end{array} \right.
Tính \mathop {{\rm{lim}}}\limits_{x \to {0^ + }} f\left( x \right),\;\;\;\;\mathop {{\rm{lim}}}\limits_{x \to {0^ - }} \;f\left( x \right) và \mathop {{\rm{lim}}}\limits_{x \to 0} \;f\left( x \right).
Chứng minh rằng \lim {\left( {\frac{e}{\pi }} \right)^n} = 0.
Chứng minh rằng \lim \frac{{ - 4n + 1}}{n} = - 4.
Chứng minh rằng:
a) \lim 0 = 0;
b) \lim \frac{1}{{\sqrt n }} = 0.
Hình 2 biểu diễn các số hạng của dãy số \left( {{u_n}} \right), với {u_n} = \frac{1}{n} trên hệ trục tọa độ.
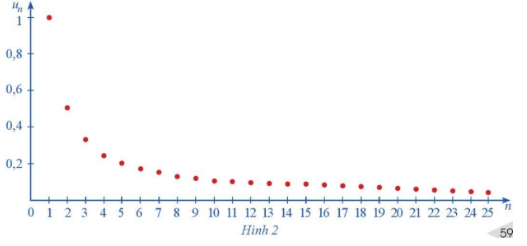
a) Nhận xét về sự thay đổi các giá trị {u_n} khi n ngày càng lớn.
b) Hoàn thành bảng và trả lời câu hỏi sau:
Kể từ số hạng {u_n} nào của dãy số thì khoảng cách từ {u_n} đến 0 nhỏ hơn 0,001? 0,0001?
Sử dụng định nghĩa, tìm các giới hạn sau:
a) \mathop {\lim }\limits_{x \to - 3} {x^2};
b) \mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}}.
Tìm các giới hạn sau:
a) \lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right);
b) \lim \left( {\frac{{1 - 4n}}{n}} \right).
Cho dãy số \left( {{u_n}} \right) với {u_n} = \frac{{2n + 1}}{n}.
a) Cho dãy số \left( {{v_n}} \right) với {v_n} = {u_n} - 2. Tìm giới hạn \lim {v_n}.
b) Biểu diễn các điểm {u_1},{u_2},{u_3},{u_4} trên trục số. Có nhận xét gì về vị trí của các điểm {u_n} khi n trở nên rất lớn?
Tính các giới hạn sau:
a) \lim \frac{1}{{{n^2}}};
b) \lim {\left( { - \frac{3}{4}} \right)^n}.
Cho dãy số \left( {{u_n}} \right) với .{u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}.
a) Tìm các giá trị còn thiếu trong bảng sau:

b) Với n thế nào thì \left| {{u_n}} \right| bé hơn 0,01; 0,001?
c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm {u_n} đến điểm 0 khi n trở nên rất lớn?
Tìm các giới hạn sau:
a) \lim \frac{{ - 2n + 1}}{n}
b) \lim \frac{{\sqrt {16{n^2} - 2} }}{n}
c) \lim \frac{4}{{2n + 1}}
d) \lim \frac{{{n^2} - 2n + 3}}{{2{n^2}}}
Tìm các giới hạn sau:
a) \lim \frac{{3n - 1}}{n}
b) \lim \frac{{\sqrt {{n^2} + 2} }}{n}
c) \lim \frac{2}{{3n + 1}}
d) \lim \frac{{\left( {n + 1} \right)\left( {2n + 2} \right)}}{{{n^2}}}
Tìm các giới hạn sau:
a) \lim \left( {2 + \frac{5}{n}} \right);
b) \lim \left( {\frac{3}{n} - \frac{2}{{{n^2}}}} \right);
c) \lim \left( {3 - \frac{4}{n}} \right)\left( {2 + \frac{5}{{{n^2}}}} \right);
d) \lim \frac{{3 - \frac{3}{n}}}{{1 + \frac{1}{{{n^3}}}}}.
Tìm các giới hạn sau:
a) \lim \frac{{2n - 3}}{{6n + 1}};
b) \lim \frac{{3n - 1}}{{{n^2} + n}};
c) \lim \frac{{\left( {2n - 1} \right)\left( {2n + 3} \right)}}{{2{n^2} + 4}};
d) \lim \frac{{4n + 1}}{{\sqrt {{n^2} + 3n} + n}};
e) \lim \sqrt n \left( {\sqrt {n + 1} - \sqrt n } \right);
g) \lim \frac{1}{{\sqrt {{n^2} + n} - n}}.
Tìm các giới hạn sau:
a) \lim {\left( {\frac{{\sqrt 3 }}{2}} \right)^n};
b) \lim \frac{{{3^n}}}{{{4^n} - 1}};
c) \lim \frac{{{3^n} - {2^n}}}{{{3^n} + {2^n}}};
d) \lim \frac{{{4^{n + 1}}}}{{{3^n} + {4^n}}}.
Cho hai dãy số \left( {{u_n}} \right) và \left( {{v_n}} \right) có \lim {u_n} = 3,\lim {v_n} = 4. Tìm các giới hạn sau:
a) \lim \left( {3{u_n} - 4} \right);
b) \lim \left( {{u_n} + 2{v_n}} \right);
c) \lim {\left( {{u_n} - {v_n}} \right)^2};
d) \lim \frac{{ - 2{u_n}}}{{{v_n} - 2{u_n}}}.
Cho dãy số \left( {{u_n}} \right) thỏa mãn n{u_n} = 3. Tìm giới hạn \lim \frac{{2n + 3}}{{{n^2}{u_n}}}.
Tùy theo giá trị của a > 0, tìm giới hạn \lim \frac{{{a^n}}}{{{a^n} + 1}}.
\lim \frac{{3{n^2} + 2n}}{{2 - {n^2}}} bằng
A. \frac{3}{2}.
B. - 2.
C. 3.
D. - 3.
\lim \frac{{\sqrt {4{n^2} + 4n + 1} }}{{4n + 1}} bằng
A. \frac{1}{2}.
B. 1.
C. 2.
D. + \infty .
\lim \frac{{2n + 1}}{{\sqrt {9{n^2} + 1} - n}} bằng
A. \frac{2}{3}.
B. 1.
C. \frac{1}{4}.
D. 2.
Cho hai dãy số \left( {{u_n}} \right) và \left( {{v_n}} \right) thỏa mãn \lim {u_n} = 4,\lim \left( {{v_n} - 3} \right) = 0. \lim \left[ {{u_n}\left( {{u_n} - {v_n}} \right)} \right] bằng
A. 7.
B. 12.
C. 4.
D. 28.
\lim \frac{{{4^n}}}{{{{2.4}^n} + {3^n}}} bằng
A. \frac{1}{2}.
B. 1.
C. 4.
D. 0.
Tìm các giới hạn sau:
a) \lim \frac{{n\left( {2{n^2} + 3} \right)}}{{4{n^3} + 1}};
b) \lim \left[ {\sqrt n \left( {\sqrt {n + 5} - \sqrt {n + 1} } \right)} \right].













