Nội dung từ Loigiaihay.Com
a) Chứng tỏ rằng hàm số \(g(x) = {x^3}\)là hàm số lẻ.
b) Cho ví dụ về hàm số không là hàm số chẵn cũng không là hàm số lẻ.
Sử dụng định nghĩa hàm số chẵn, hàm số lẻ.

a)
Hàm số \(g(x) = {x^3}\)
+) Có tập xác định D = R;
+) Với mọi \(x \in R\)thì \( - x \in R\)
Ta có \(g( - x) = {\left( { - x} \right)^3} = - {x^3} = - g(x)\)
Vậy \(g(x) = {x^3}\)là hàm số lẻ.
b)
Ví dụ về hàm số không là hàm số chẵn không là hàm số lẻ là
\(f(x) = {x^3} + {x^2}\)

Các bài tập cùng chuyên đề
Bài 1 :
Xét tính tuần hoàn của hàm số \(y = \tan 2x\).
Bài 2 :
So sánh:
a) \(\sin \left( {x + 2\pi } \right)\) và \(\sin x\);
b) \(\cos (x + 2\pi )\) và \(\cos x\);
c) \(\tan \left( {x + \pi } \right)\) và \(\tan x\);
d) \(\cot (x + \pi )\) và \(\cot x\).
Bài 3 :
Xét tính chẵn, lẻ của hàm số \(g\left( x \right) = \frac{1}{x}\).
Bài 4 :
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
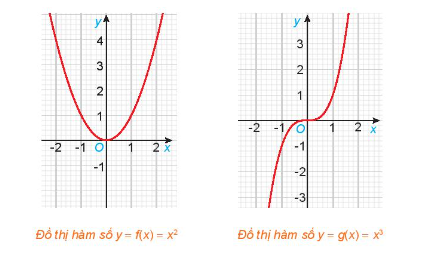
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
Bài 5 :
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = \sin 2x + \tan 2x\);
b) \(y = \cos x + {\sin ^2}x\);
c) \(y = \sin x\cos 2x\);
d) \(y = \sin x + \cos x\).
Bài 6 :
Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn?
A. \(y = \tan x + x\)
B. \(y = {x^2} + 1\)
C. \(y = \cot x\)
D. \(y = \frac{{\sin x}}{x}\)
Bài 7 :
Cho ví dụ về hàm số tuần hoàn
Bài 8 :
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như Hình 22.
a) Có nhận xét gì về đồ thị hàm số trên mỗi đoạn \(\left[ {a;a + T} \right],\left[ {a + T;a + 2T} \right],\left[ {a - T;a} \right]\)?
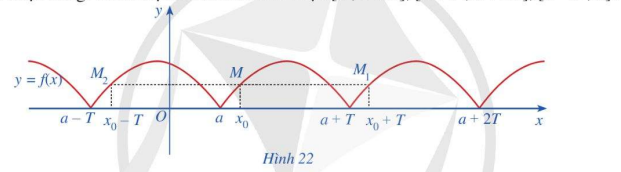
b) Lấy điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) thuộc đồ thị hàm số với \({x_0} \in \left[ {a;a + T} \right]\). So sánh mỗi giá trị \(f\left( {{x_0} + T} \right);f\left( {{x_0} - T} \right)\) với \(f\left( {{x_0}} \right)\)
Bài 9 :
a) Cho hàm số \(f\left( x \right) = {x^2}\)
Với \(x \in \mathbb{R}\), hãy so sánh \(f\left( { - x} \right)\) và \(f\left( x \right)\)
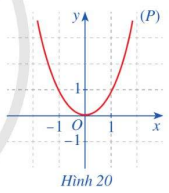
Quan sát parabol (P) là đồ thị của hàm số \(f\left( x \right) = {x^2}\) (Hình 20) và cho biết trục đối xứng của (P) là đường thẳng nào?
b) Cho hàm số \(g\left( x \right) = x\)
Với \(x \in \mathbb{R}\), hãy so sánh \(g\left( { - x} \right)\) và \(g\left( x \right)\)
Quan sát đường thẳng d là đồ thị của hàm số \(g\left( x \right) = x\) (Hình 21) và cho biết gốc tọa độ O có là tâm đối xứng của đường thẳng d hãy không.

Bài 10 :
Xét tính chẵn, lẻ của các hàm số:
a) \(y = \sin x\cos x\)
b) \(y = \tan x + \cot x\)
c) \(y = {\sin ^2}x\)
Bài 11 :
Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx
Bài 12 :
Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi \(x \in \mathbb{R}\).
Bài 13 :
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.
Bài 14 :
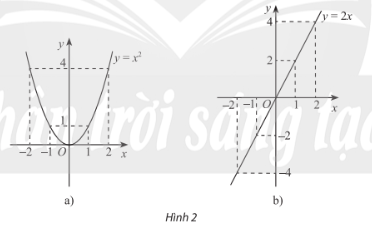
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
Bài 15 :
a, \(y = 5si{n^2}\alpha + 1\)
b, \(y = cosx + sinx\)
c, \(y = tan2x\)
Bài 16 :
Khẳng định nào sau đây là đúng?
A. Hàm số y = sinx là hàm số chẵn.
B. Hàm số y = cosx là hàm số chẵn
C. Hàm số y = tanx là hàm số chẵn
D. Hàm số y = cotx là hàm số chẵn
Bài 17 :
Hàm số nào sau đây là hàm số chẵn?
-
A.
\(y = - \cos x\)
-
B.
\(y = - 2\sin x\)
-
C.
\(y = 2\sin ( - x)\)
-
D.
\(y = \sin x - \cos x\)
Bài 18 :
Hàm số nào sau đây là hàm số chẵn?
-
A.
\(y = \left| {\sin x} \right|\)
-
B.
\(y = {x^2}.\sin x\)
-
C.
\(y = \frac{x}{{\cos x}}\)
-
D.
\(y = x + \sin x\)
Bài 19 :
Khẳng định nào sau đây là sai?
-
A.
Hàm số \(y = \sin x\) là hàm số lẻ
-
B.
Hàm số \(y = \cos x\) là hàm số lẻ
-
C.
Hàm số \(y = \tan x\) là hàm số lẻ
-
D.
Hàm số \(y = \cot x\) là hàm số lẻ
Bài 20 :
Hàm số \(y = f\left( x \right)\) (có tập xác định \(D\)) là hàm số lẻ nếu với \(\forall x \in D\) thì \( - x \in D\) và
-
A.
\(f\left( { - x} \right) = f\left( x \right)\)
-
B.
\(f\left( { - x} \right) = - f\left( x \right)\)
-
C.
\(f\left( { - x} \right) = f\left( {\pi x} \right)\)
-
D.
\(f\left( { - x} \right) = - f\left( {\pi x} \right)\)
Bài 21 :
Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) là hàm số tuần hoàn nếu tồn tại một số \(T\) khác \(0\) sao cho \(\forall x \in D\) ta có \(x + T \in D,x - T \in D\) và
-
A.
\(f\left( {x + T} \right) = f\left( x \right)\)
-
B.
\(f\left( {x + T} \right) = - f\left( x \right)\)
-
C.
\(f\left( {x + T} \right) = 2\pi f\left( x \right)\)
-
D.
\(f\left( {x + T} \right) = - 2\pi f\left( x \right)\)
Bài 22 :
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = \frac{{\cos 2x}}{{{x^3}}}\);
b) \(y = x - \sin 3x\);
c) \(y = \sqrt {1 + \cos x} \);
d) \(y = 1 + \cos x\sin \left( {\frac{{3\pi }}{2} - 2x} \right)\).
Bài 23 :
Xét tính tuần hoàn của các hàm số sau:
a) \(y = {\rm{A}}\sin \left( {\omega x + \varphi } \right)\) với A > 0;
b) \(y = {\rm{A}}\tan \left( {\omega x + \varphi } \right)\) với A > 0;
c) \(y = 3\sin 2x + 3\cos 2x\);
d) \(y = 3\sin \left( {2x + \frac{\pi }{6}} \right) + 3\sin \left( {2x - \frac{\pi }{3}} \right)\).
Bài 24 :
Mệnh đề nào sau đây sai?
A. Hàm số \(y = \sin x\) tuần hoàn với chu kì \(2\pi \).
B. Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi \).
C. Hàm số \(y = \tan x\) tuần hoàn với chu kì \(2\pi \).
D. Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi \).
Bài 25 :
Mệnh đề nào sau đây sai?
A. Hàm số \(y = \sin x\cos 2x\) là hàm số tuần hoàn.
B. Hàm số \(y = \sin x\cos 2x\) là hàm số lẻ.
C. Hàm số \(y = x\sin x\) là hàm số tuần hoàn.
D. Hàm số \(y = x\sin x\) là hàm số chẵn.
Bài 26 :
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = {\sin ^3}x - \cot x;\)
b) \(y = \frac{{\cos x + {{\tan }^2}x}}{{\cos x}}\);
c) \(y = \sin 2x + \cos x\);
d) \(y = 2\cos \left( {\frac{{3\pi }}{4} + x} \right)\sin \left( {\frac{\pi }{4} - x} \right)\).
Bài 27 :
Xét tính tuần hoàn của các hàm số sau:
a) \(y = \sin \frac{x}{2} + \cos 3x\);
b) \(y = \cos 5x + \tan \frac{x}{3}\).
Bài 28 :
Hàm số nào sau đây là hàm số lẻ?
A. \(y = - 2\cos x\)
B. \(y = - 2\sin x\)
C. \(y = \tan x - \cos x\)
D. \(y = - 2\sin x + 2\)
Bài 29 :
Hàm số nào sau đây là hàm số chẵn?
A. \(y = \cos x + 5\)
B. \(y = \tan x + \cot x\)
C. \(y = \sin \left( { - x} \right)\)
D. \(y = \sin x - \cos x\)
Bài 30 :
Xét tính chẵn, lẻ của các hàm số sau:
a) \(y = \sin 2x\)
b) \(y = \left| {\sin x} \right|\)
c) \(y = {\tan ^2}x\)
d) \(y = \sqrt {1 - \cos x} \)
e) \(y = \tan x + \cot x\)
f) \(y = \sin x\cos 3x\)












