Nội dung từ Loigiaihay.Com
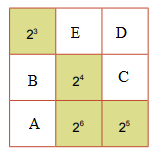
Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.
Tính tích của 3 ô in đậm ở đường chéo đã biết. Tích này chính là tích của từng hàng , cột.
Tính hàng, cột khi biết tích của hàng, cột và 2 ô của hàng, cột đó.
Ta đặt các ô chưa biết như sau:
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là:


Các bài tập cùng chuyên đề
Viết số \({({2^2})^3}\) dưới dạng lũy thừa cơ số 2 và số \({\left[ {{{( - 3)}^2}} \right]^2}\) dưới dạng lũy thừa cơ số \(-3\).
Viết các số \({\left( {\frac{1}{4}} \right)^8};{\left( {\frac{1}{8}} \right)^3}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
Tính và so sánh.
a)\({\left[ {{{\left( { - 2} \right)}^2}} \right]^3}\) và \({\left( { - 2} \right)^6}\) b) \({\left[ {{{\left( {\frac{1}{2}} \right)}^2}} \right]^2}\) và \({\left( {\frac{1}{2}} \right)^4}\).
Thay số thích hợp thay vào dấu “?” trong các câu sau:
a)\({\left[ {{{\left( {\frac{{ - 2}}{3}} \right)}^2}} \right]^5} = {\left( {\frac{{ - 2}}{3}} \right)^?};\) b)\({\left[ {{{\left( {0,4} \right)}^3}} \right]^3} = {\left( {0,4} \right)^?}\) c)\({\left[ {{{\left( {7,31} \right)}^3}} \right]^0} = ?\)
Để viết những số có giá trị lớn, người ta thường viết các số ấy dưới dạng tích của luỹ thừa cơ số 10 với một số lớn hơn hoặc bằng 1 nhưng nhỏ hơn 10. Chẳng hạn khoảng cách trung bình giữa Mặt Trời và Trái Đất là 149 600 000 km được viết là 1,496 . 108 km.
Hãy dùng cách viết trên để viết các đại lượng sau:
a) Khoảng cách từ Mặt Trời đến Sao Thuỷ dài khoảng 58 000 000 km.
b) Một năm ánh sáng có độ dài khoảng 9 460 000 000 000 km.
(Theo: https://vi.wikipedia.org/wiki/Hệ Mặt Trời)
Viết các số \({\left( {0,25} \right)^8};\,\,{\left( {0,125} \right)^4};{\left( {0,0625} \right)^2}\)dưới dạng lũy thừa cơ số 0,5.
So sánh: \({\left( {{{15}^3}} \right)^2}\) và \({15^{3.2}}\).
Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa của a:
a)\({\left[ {{{\left( { - \frac{1}{6}} \right)}^3}} \right]^4}\) với \(a = - \frac{1}{6}\).
b)\({\left[ {{{\left( { - 0,2} \right)}^4}} \right]^5}\) với \(a = - 0,2\).
Cho \(x\) là số hữu tỉ. Viết \({x^{12}}\) dưới dạng:
a) Luỹ thừa của \({x^2}\);
b) Luỹ thừa của \({x^3}\).

Giá trị của \({\left( {{2^3}} \right)^5}\) :
A.\({2^8};\)
B.\({2^{15}};\)
C.\({\left( {\frac{1}{2}} \right)^{28}};\)
D.\(\frac{1}{2}\)
Số tự nhiên n thỏa mãn \(\left[(0,25)^4 \right]^3 =(0,25)^n\) là:
Viết số \({\left( {\frac{1}{9}} \right)^4}\) dưới dạng luỹ thừa cơ số \(\frac{1}{3}\) ta được
Giá trị của \({({2^3})^2}\) bằng