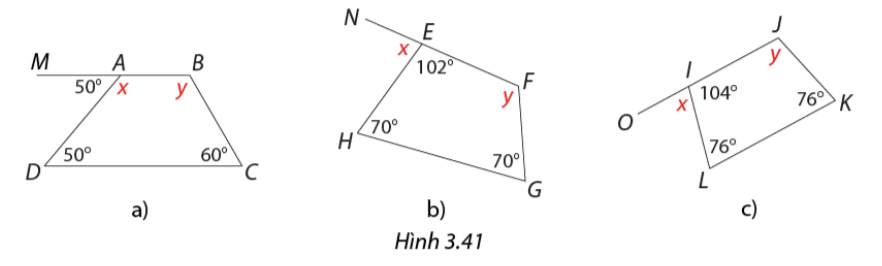
Trong các tứ giác ở Hình 3.41; tứ giác nào là hình thang, hình thang cân? Tính các số đo góc \(x,y\) trong mỗi trường hợp.

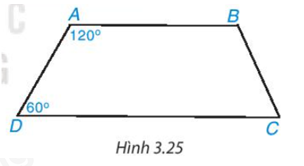
Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

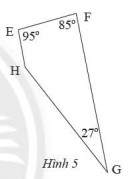
Tứ giác \(EFGH\) có các góc cho như trong Hình 5.

a) Chứng minh rằng \(EFGH\) là hình thang

b) Tìm góc chưa biết của tứ giác

Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo  \(\widehat A\) và \(\widehat B\).

Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.

a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)

b) \(\widehat P = \widehat Q = 110^\circ \)

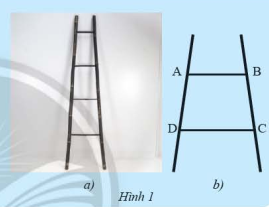
Tứ giác \(ABCD\) (Hình 1b) là hình vẽ minh họa một phần của chiếc thang ở Hình 1a. Nêu nhận xét của em về hai cạnh \(AB\) và \(CD\) của tứ giác này.

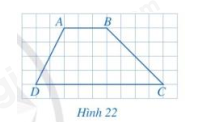
Cho biết hai cạnh AB và CD của tứ giác ABCD ở Hình 22 có song song với nhau hay không?

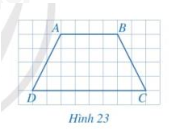
Hai góc C và D cùng kề với đáy CD của hình thang ABCD ở Hình 23. Cho biết hai góc C và D có bằng nhau hay không?

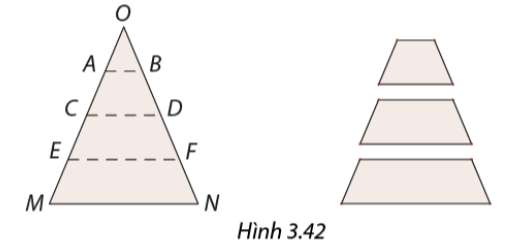
Mai cắt mảnh giấy hình tam giác cân \(OMN\) theo các đường song song với cạnh đáy (Hình 3.42). Vì sao các tứ giác thu được là hình thang cân?

Chứng minh rằng trong hình thang có nhiều nhất hai góc tù.

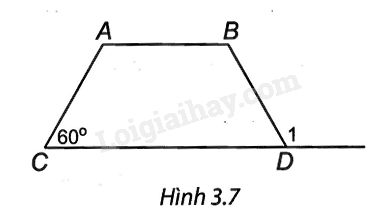
Cho hình thang ABCD cân (AB // CD) có \(\widehat C = {60^0}\) (H.3.7). Khi đó, số đo \(\widehat {{D_1}}\) bằng:

 A. \(60^\circ \)

B. \(80^\circ \)

C. \(120^\circ \)

D. \(100^\circ \)

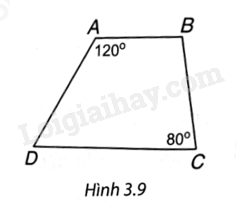
Hình thang trong Hình 3.9 có là hình thang cân không? Vì sao?

Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Cho hình thang cân ABCD có AB // CD và \(\widehat A = 125^\circ \). Khi đó số đo góc C là

Câu nào sau đây là đúng khi nói về hình thang:

Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường cao AH = 5cm và \(\widehat {BCD} = 45^\circ \). Độ dài đáy lớn CD là: