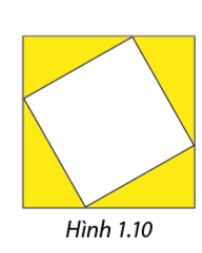
Một người dùng các thanh kim loại để thiết kế một khung ảnh gồm hai hình vuông lồng vào nhau như Hình 1.10, trong đó ảnh được gắn vào hình vuông nhỏ. Biết rằng tổng chiều dài của các thanh kim loại để làm khung là \(168\,\,cm\) và diện tích phần không gắn ảnh( phần tô màu) là \(252\,\,c{m^2}\). Tính diện tích của phần được gắn ảnh. 

Quan sát Hình 2.1

a)      Tính diện tích của phần hình màu xanh ở Hình 2.1a.

b)      Tính diện tích hình chữ nhật màu xanh ở Hình 2.1b.

c)      Có nhận xét gì về diện tích của hai hình ở câu a và câu b?

Với hai số a,b bất kì, thực hiện phép tính \(\left( {a + b} \right)\left( {a - b} \right)\).

Từ đó rút ra liên hệ giữa \({a^2} - {b^2}\) và \(\left( {a + b} \right)\left( {a - b} \right)\).

a)      Tính nhanh \({99^2} - 1\)

b)      Viết \({x^2} - 9\) dưới dạng tích.

Ở bài toán mở đầu, em hãy giải thích xem bạn đó tính nhanh như thế nào.

Chứng minh rằng với mọi số tự nhiên n, ta có:

\({\left( {n + 2} \right)^2} - {n^2}\) chia hết cho 4.

1. Viết đa thức \({x^3} - 8\) dưới dạng tích.
2. Rút gọn biểu thức \(\left( {3x - 2y} \right)\left( {9{x^2} + 6xy + 4{y^2}} \right) + 8{y^3}\)

Khẳng định nào sau đây là đúng?

A. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + 2AB + {B^2}\)

B. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - 2AB + {B^2}\)

C. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + {B^2}\)

D. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - {B^2}\)

a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.

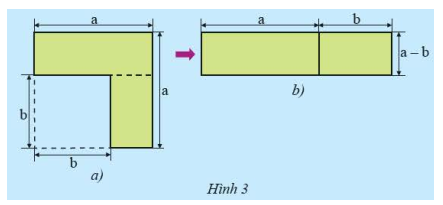
b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?

Thực hiện các phép nhân:

a) \(\left( {4 - x} \right)\left( {4 + x} \right)\)                                   

b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right)\)                      

c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right)\)

Tính nhanh:

a) \(82.78\)                                          

b) \(87.93\)                             

c) \({125^2} - {25^2}\)

Giải đáp câu hỏi ở đầu bài (trang 18)

Viết các biểu thức sau thành đa thức:

a) \(\left( {3x - 5} \right)\left( {3x + 5} \right)\)                               

b) \(\left( {x - 2y} \right)\left( {x + 2y} \right)\)                      

c) \(\left( { - x - \dfrac{1}{2}y} \right)\left( { - x + \dfrac{1}{2}y} \right)\)

Viết các biểu thức sau thành đa thức:

a) \(\left( {a - 1} \right)\left( {a + 1} \right)\left( {{a^2} + 1} \right)\)                    b) \({\left( {xy + 1} \right)^2} - {\left( {xy - 1} \right)^2}\)

Với a, b là hai số thực bất kì, thực hiện phép tính: \(\left( {a - b} \right)\left( {a + b} \right)\)

Viết mỗi biểu thức sau dưới dạng tích:

a) \(9{{\rm{x}}^2} - 16\)

b) \(25 - 16{y^2}\)

Tính:

\(a)\left( {a - 3b} \right)\left( {a + 3b} \right)\)

\(b)\left( {2{\rm{x}} + 5} \right)\left( {2{\rm{x}} - 5} \right)\)

\(c)\left( {4y - 1} \right)\left( {4y + 1} \right)\)

Tính nhanh: \(48.52\).

Cho \(a\) và \(b\) là hai số thực bất kì.

1. \(\left( {a + b} \right)\left( {a - b} \right)\).

2. Hãy cho biết: \({a^2} - {b^2} = ?\)

a) \(\left( {2a + 1} \right)\left( {2a - 1} \right)\)

b)\(\left( {2x + 5y} \right)\left( {2x - 5y} \right)\)

Tính nhanh:

a) \(49.51\)

b) \({32^2} - 128 + 4\)

a) Tính giá trị của \({u^2} - {v^2},\) biết rằng \(u - v = 3\) và \(u + v = 7.\)

b) Tính giá trị của \(u - v,\) biết rằng \({u^2} - {v^2} = 20\) và \(u + v = 5.\)

Chứng minh rằng \({9^n} - 1\) chia hết cho \({3^n} - 1\) với mọi số nguyên dương \(n\)

Tính nhanh:

a) \({202^2}\)

b) \(299.301\)

c) \({95^3} + {15.95^2} + 3.95.25 + {5^3}\)

d) \(9\left( {{{10}^2} + 10 + 1} \right) + 100\left( {{{98}^2} + 392 + {2^2}} \right)\)

Không tính giá trị của biểu thức, hãy so sánh:

a) \(M = 2021.2023\) và \(N = {2022^2}\)

b) \(P = 3\left( {{2^2} + 1} \right)\left( {{2^4} + 1} \right)\left( {{2^8} + 1} \right) + 2\) và \(Q = {\left( {{2^2}} \right)^8}\)

Viết các biểu thức sau thành đa thức:

a) \(\left( {1 - 4x} \right)\left( {1 + 4x} \right)\);

b) \(\left( { - 2x - 5y} \right)\left( {2x - 5y} \right)\);

c) \(\left( {{x^3} - 3x} \right)\left( {3x + {x^3}} \right)\);

d) \(\left( {1 + x + {x^2}} \right)\left( {1 + x - {x^2}} \right)\).

Chứng minh rằng, với mọi số nguyên n

a) \((2n + 1)^2 − (2n − 1)^2\) chia hết cho 8;

b) \((8n + 4)^2 − (2n + 1)^2\) chia hết cho 15.

Viết các biểu thức sau thành đa thức:

a) \(\left( {{x^2} + 4{y^2}} \right)\left( {x + 2y} \right)\left( {x - 2y} \right)\);

b) \(\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)\left( {{x^4} + 1} \right)\).

Đa thức \(4{x^2}\;-1\) được viết dưới dạng tích của hai đa thức

A. \(2x-1\) và \(2x + 1\).

B. \(x-1\) và \(4x + 1\).

C. \(2x-1\) và \(2x-1\).

D. \(x + 1\) và \(4x-1\).

Khẳng định nào sau đây là đúng?

A. \(\left( {A-B} \right)\left( {A-B} \right) = {A^2}\; + 2AB + {B^2}\).

B. \(\left( {A + B} \right)\left( {A + B} \right) = {A^2}\;-2AB + {B^2}\).

C. \(\left( {A + B} \right)\left( {A-B} \right) = {A^2}\; + {B^2}\).

D. \(\left( {A + B} \right)\left( {A-B} \right) = {A^2}\;-{B^2}\).

Tính nhanh

a) \({101^2}\;-1\).

b) \({2003^2}\;-9\).