Nội dung Tổng hợp
Một vật chuyển động với vận tốc được cho bởi đồ thị ở Hình 9.
a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên
b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên
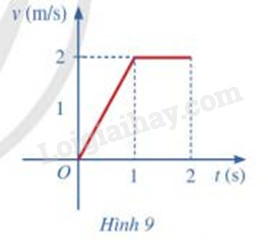
Xác định vận tốc ở các khoảng thời gian và tính toán quãng đường thông qua tích phân
a) Trong 1 giây đầu tiên, vận tốc được biểu diễn bởi hàm số: v(t)=2t
Quãng đường mà vật di chuyển được trong 1 giây đầu tiên: s(1)=1∫0v(t)dt=1∫02tdt=1 (m)
b) Trong 1 giây tiếp theo, v=2(m/s)
Quãng đường mà vật di chuyển được trong 2 giây đầu tiên: s(2)=1∫0v(t)dt+2∫1v(t)dt=1∫02tdt+1∫02dt=3 (m)

Các bài tập cùng chuyên đề
Bài 1 :
Tính tích phân 3∫21x2dx có giá trị bằng:
A. 16
B. −16
C. 19648
D. −19648
Bài 2 :
Tích phân π5∫π7sinxdx có giá trị bằng:
Bài 3 :
Tích phân I=1∫03x2dx có giá trị bằng:
A. −1ln3
B. 1ln3
C. -1
D. 1
Bài 4 :
Tính:
a) 1∫0(x6−4x3+3x2)dx
b) 2∫11x4dx
c) 4∫11x√xdx
d) π2∫0(4sinx+3cosx)dx
e) π2∫π4cot2xdx
g) π4∫0tan2xdx
h) 0∫−1e−xdx
i) −1∫−2ex+2dx
k) 1∫0(3.4x−5e−x)dx
Bài 5 :
a) Cho một vật chuyển động với vận tốc y = v(t) (m/s). Cho 0 < a < b và v(t) > 0 với mọi t∈[a;b]. Hãy giải thích vì sao b∫av(t)dt biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b (a,b tính theo giây).
b) Áp dụng công thức ở câu a) để giải bài toán sau: một vật chuyển động với vận tốc v(t) = 2 – sint (m/s). Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm t = 0 (s) đến thời điểm t=3π4 (s).
Bài 6 :
Ở nhiệt độ 37∘C, một phản ứng hóa học từ chất đầu A, chuyển hóa thành sản phẩm B theo phương trình: A→B. Giả sử y(x) là nồng độ chất A (đơn vị mol L−1) tại thời gian x (giây), y(x) > 0 với x≥0, thỏa mãn hệ thức y′(x)=−7.10−4y(x) với x≥0. Biết rằng tại x = 0, nồng độ (đầu) của A là 0,05 mol L−1.
a) Xét hàm số f(x)=lny(x) với x≥0. Hãy tính f’(x), từ đó hãy tìm hàm số f(x).
b) Giả sử tính nồng độ trung bình chất A (đơn vị mol L−1) từ thời điểm a(giây) đến thời điểm b(giây) với 0 < a < b theo công thức 1b−ab∫ay(x)dx. Xác định nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây.
Bài 7 :
Tính các tích phân sau:
a) 2∫1x4dx
b) 2∫11√xdx
c) π4∫01cos2xdx
d) 2∫03xdx
Bài 8 :
Tính các tích phân sau:
a) 1∫0(1−2x)2dx;
b) 4∫1x−2√xdx.
Bài 9 :
Tính các tích phân sau:
a) 2∫0|2x−1|dx;
b) 3∫−2|x−1|dx.
Bài 10 :
Tính các tích phân sau:
a) π2∫0(3cosx+2sinx)dx;
b) π4∫π6(1cos2x−1sin2x)dx.
Bài 11 :
Tính các tích phân sau:
a) 1∫0(3x−2ex)dx;
b) 1∫0(ex−1)22exdx.
Bài 12 :
Phát biểu nào sau đây là đúng?
A. b∫asinxdx=sina−sinb.
B. b∫asinxdx=sinb−sina.
C. b∫asinxdx=cosa−cosb.
D. b∫asinxdx=cosb−cosa.
Bài 13 :
Phát biểu nào sau đây là đúng? Biết f(x)=1sin2x liên tục trên [a;b].
A. b∫a1sin2xdx=cota−cotb.
B. b∫a1sin2xdx=cotb−cota.
C. b∫a1sin2xdx=tana−tanb.
D. b∫a1sin2xdx=tanb−tana.
Bài 14 :
Tích phân 2∫1−3x3dx có giá trị bằng:
A. 98.
B. −4564.
C. 158.
D. −98.
Bài 15 :
Tích phân 2∫11x√xdx có giá trị bằng:
A. 2−√2.
B. 2+√2.
C. −√2+820.\
D. −√2−820.
Bài 16 :
Phát biểu nào sau đây là đúng?
A. b∫acosxdx=sina−sinb.
B. b∫acosxdx=sinb−sina.
C. b∫acosxdx=cosa−cosb.
D. b∫acosxdx=cosb−cosa.
Bài 17 :
Phát biểu nào sau đây là đúng? Biết f(x)=1cos2x liên tục trên [a;b].
A. b∫a1cos2xdx=cota−cotb.
B. b∫a1cos2xdx=cotb−cota.
C. b∫a1cos2xdx=tana−tanb.
D. b∫a1cos2xdx=tanb−tana.
Bài 18 :
Cho m thoả mãn m>0,m≠1. Phát biểu nào sau đây là đúng?
A. b∫amxdx=mb−ma.
B. b∫amxdx=ma−mb.
C. b∫amxdx=mblnm−malnm.
D. b∫amxdx=malnm−mblnm.
Bài 19 :
Tính:
a) 1∫0−2dx;
b) 1∫02x3dx;
c) 1∫0x4dx;
d) 3∫123√xdx;
e) 2∫123xdx;
g) 9∫1(x√x−2)dx.
Bài 20 :
Tính:
a) π2∫0sinxdx;
b) π4∫0cosxdx;
c) π2∫π41sin2xdx;
d) π4∫01cos2xdx;
e) π2∫0(sinx−2)dx;
g) π4∫0(3cosx+2)dx.
Bài 21 :
Tính:
a) 2∫0e−5xdx;
b) 1∫03x+2dx;
c) 1∫−132xdx.
Bài 22 :
Tính các tích phân sau:
a) 2∫0(3x−2)(3x+2)dx;
b) 2∫1t2(5t2−2)dt;
c) 1∫−1(x−2)(x2+2x+4)dx.
Bài 23 :
Tính các tích phân sau:
a) \int\limits_1^2 {\frac{{1 - 2{\rm{x}}}}{{{x^2}}}dx} ;
b) \int\limits_1^2 {{{\left( {\sqrt x + \frac{1}{{\sqrt x }}} \right)}^2}dx} ;
c) \int\limits_1^4 {\frac{{x - 4}}{{\sqrt x + 2}}dx} .
Bài 24 :
Tính các tích phân sau:
a) \int\limits_1^3 {{e^{x - 2}}dx} ;
b) \int\limits_0^1 {{{\left( {{2^x} - 1} \right)}^2}dx} ;
c) \int\limits_0^1 {\frac{{{e^{2x}} - 1}}{{{e^x} + 1}}dx} .
Bài 25 :
Tính các tích phân sau:
a) \int\limits_0^\pi {\left( {2\cos x + 1} \right)dx} ;
b) \int\limits_0^\pi {\left( {1 + \cot x} \right)\sin xdx} ;
c) \int\limits_0^{\frac{\pi }{4}} {{{\tan }^2}xdx} .
Bài 26 :
Cho hàm số f\left( x \right) có đạo hàm f'\left( x \right) = \frac{{\sqrt x - 1}}{x},x > 0. Tính giá trị của f\left( 4 \right) - f\left( 1 \right).
Bài 27 :
Tìm đạo hàm của hàm số F\left( x \right) = \sqrt {4x + 1} . Từ đó, tính tích phân \int\limits_0^1 {\frac{1}{{\sqrt {4x + 1} }}dx} .
Bài 28 :
Tính:
a) \int\limits_1^2 {\frac{{{x^4} + {x^3} + {x^2} + x + 1}}{{{x^2}}}dx} ;
b) \int\limits_1^2 {\frac{{x{e^x} + 1}}{x}dx} ;
c) \int\limits_0^1 {\frac{{{8^x} + 1}}{{{2^x} + 1}}dx} ;
d) \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{{1 + {{\sin }^2}x}}{{1 - {{\cos }^2}x}}dx} .
Bài 29 :
Tính
a) \int\limits_1^3 {{x^3}dx;}
b) \int\limits_0^\pi {\cos udu.}
Bài 30 :
a) Cho hàm số f(x) liên tục trên đoạn [ - 1;5] và \int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx = 12. Tính \int_{ - 1}^5 f (x)dx.
b) Cho f(x) = \left\{ {\begin{array}{*{20}{l}}{{x^3} + 2}&{{\rm{khi }}x > - 1}\\{2x + 3}&{{\rm{khi }}x \le - 1}\end{array}} \right.. Tính \int_{ - 2}^1 f (x)dx.












