Nội dung từ Loigiaihay.Com
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’, với \(A\left( {1; - 1;3} \right),B\left( {0;2;4} \right),\)\(D\left( {2; - 1;1} \right),A'\left( {0;1;2} \right)\).
a) Tìm tọa độ các điểm C, B’, D’.
b) Viết phương trình mặt phẳng (CB’D’).
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
+ Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \)
+ Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \).
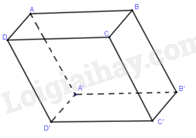
a) \(\overrightarrow {AB} \left( { - 1;3;1} \right),\overrightarrow {AA'} \left( { - 1;2; - 1} \right)\)
Vì ABCD.A’B’C’D’ là hình hộp nên
+) \(\overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - {x_{A'}} = - 1\\{y_{B'}} - {y_{A'}} = 3\\{z_{B'}} - {z_{A'}} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{B'}} = - 1 + {x_{A'}} = - 1 + 0 = - 1\\{y_{B'}} = 3 + {y_{A'}} = 3 + 1 = 4\\{z_{B'}} = 1 + {z_{A'}} = 1 + 2 = 3\end{array} \right. \Rightarrow B'\left( { - 1;4;3} \right)\)
+) \(\overrightarrow {AA'} = \overrightarrow {DD'} \Rightarrow \left\{ \begin{array}{l}{x_{D'}} - {x_D} = - 1\\{y_{D'}} - {y_D} = 2\\{z_{D'}} - {z_D} = - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{D'}} = - 1 + {x_D} = 1\\{y_{D'}} = 2 + {y_D} = 1\\{z_{D'}} = - 1 + {z_D} = 0\end{array} \right. \Rightarrow D'\left( {1;1;0} \right)\)
+) \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left\{ \begin{array}{l} - 1 = {x_C} - {x_D}\\3 = {y_C} - {y_D}\\1 = {z_C} - {z_D}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_C} = - 1 + {x_D} = - 1 + 2 = 1\\{y_C} = 3 + {y_D} = 3 - 1 = 2\\{z_C} = 1 + {z_D} = 1 + 1 = 2\end{array} \right. \Rightarrow C\left( {1;2;2} \right)\)
b) Ta có: \(\overrightarrow {CD'} \left( {0; - 1; - 2} \right),\overrightarrow {CB'} \left( { - 2;2;1} \right)\)
Ta có: \(\left[ {\overrightarrow {CD'} ,\overrightarrow {CB'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\2&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&0\\1&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 1}\\{ - 2}&2\end{array}} \right|} \right) = \left( {3;4; - 2} \right)\)
Mặt phẳng (CB’D’) đi qua điểm \(C\left( {1;2;2} \right)\) và nhận \(\left[ {\overrightarrow {CD'} ,\overrightarrow {CB'} } \right] = \left( {3;4; - 2} \right)\) làm một vectơ pháp tuyến. Do đó, phương trình mặt phẳng (CB’D’) là:
\(3\left( {x - 1} \right) + 4\left( {y - 2} \right) - 2\left( {z - 2} \right) = 0 \Leftrightarrow 3x + 4y - 2z - 7 = 0\)

Các bài tập cùng chuyên đề
Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.
a) Xác định tọa độ của vị trí \({M_1},{M_2},{M_3}\) của vật tương ứng với các thời điểm \(t = 0,t = \frac{\pi }{2},t = \pi \).
b) Chứng minh rằng \({M_1},{M_2},{M_3}\) không thẳng hàng và viết phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\).
c) Vị trí \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) có luôn thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) hay không?
(H.5.8) Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) \(\left( {a,b,c \ne 0} \right)\).
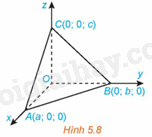
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (Phương trình trên được gọi là phương trình mặt phẳng theo đoạn chắn).
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1;2;3} \right),B\left( { - 1;3;4} \right),C\left( {2; - 1;2} \right)\)
a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Viết phương trình mặt phẳng (ABC).
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2; - 1} \right),B\left( {4;1;2} \right),C\left( {2;3;1} \right)\). Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC.
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và biết cặp vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow v = \left( {a';b';c'} \right)\).
a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
b) Viết phương trình mặt phẳng \(\left( \alpha \right)\).
Trong không gian Oxyz, viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) và vuông góc với trục Oz.
Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), \(C\left( {0;2\sqrt 2 ;0} \right)\). Bốn bức tường của căn phòng đều vuông góc với sàn.
a) Viết phương trình bốn mặt phẳng tương ứng chứa bốn bức tường đó.
b) Trong bốn mặt phẳng tương ứng chứa bốn bức tường đó, hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

Trong không gian Oxyz, viết phương trình mặt phẳng đi qua điểm \(M\left( {1;2; - 1} \right)\) và vuông góc với trục Ox.
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm \(M\left( {1; - 1;5} \right)\) và vuông góc với hai mặt phẳng \(\left( Q \right):3x + 2y - z = 0\), \(\left( R \right):x + y - z = 0\).
Trong không gian Oxyz, viết phương trình mặt phẳng đi qua điểm \(M\left( {2;3; - 1} \right)\) song song với trục Ox và vuông góc với mặt phẳng \(\left( Q \right):x + 2y - 3z + 1 = 0\).
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua điểm \(I\left( {1; - 1;2} \right)\) và nhận vectơ \(\overrightarrow n = \left( {2;1; - 1} \right)\) làm một vectơ pháp tuyến là
A. \(x - y + 2z + 1 = 0\).
B. \(x - y + 2z - 6 = 0\).
C. \(2x + y - z - 1 = 0\).
D. \(2x + y - z + 1 = 0\).
Trong không gian Oxyz, cho mặt phẳng (P): \(x - 2y - 2z - 3 = 0\) và đường thẳng d: \(\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 1}}\). Viết phương trình mặt phẳng (Q) chứa d và vuông góc với mặt phẳng (P).
Cho ba điểm H(-1;1;2), I(1;3;2), K(-1;4;5) cùng thuộc mặt phẳng (P) (Hình 11)
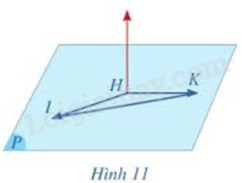
a) Tím tọa độ của các vecto \(\overrightarrow {HI} ,\overrightarrow {HK} \). Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng
b) Lập phương trình mặt phẳng (P) đi qua điểm H(-1;1;2), biết cặp vecto chỉ phương là \(\overrightarrow {HI} ,\overrightarrow {HK} \)
Cho mặt phẳng (P) đi qua điểm I(1;3;-2) có cặp vecto chỉ phương là \(\overrightarrow u = (1;1;3),\overrightarrow v = (2; - 1;2)\) (Hình 10)
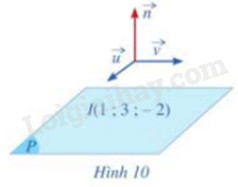
a) Hãy chỉ ra một vecto pháp tuyến \(\overrightarrow n \) của mặt phẳng (P)
b) Lập phương trình mặt phẳng (P) đi qua điểm I(1;3;-2) biết vecto pháp tuyển \(\overrightarrow n \)
Cho mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) có \(\overrightarrow n (A;B;C)\) là vecto pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9)
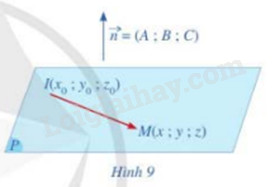
a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {IM} \)
b) Hãy biểu diễn \(\overrightarrow n .\overrightarrow {IM} \) theo \({x_0},{y_0},{z_0};x,y,z\) và A, B, C
Lập phương trình mặt phẳng (P) đi qua điểm I(3;-4;5) và nhận \(\overrightarrow n \) làm vecto pháp tuyến
Lập phương trình mặt phẳng (P) đi qua điểm K(-1;2;3) và nhận hai vecto \(\overrightarrow u = (1;2;3),\overrightarrow v = (4;5;6)\) làm cặp vecto chỉ phương
Lập phương trình mặt phẳng (P) đi qua:
a) Điểm I(3;-4;1) và vuông góc với trục Ox
b) Điểm K(-2;4;-1) và song song với mặt phẳng (Ozx)
c) Điểm K(-2;4;-1) và song song với mặt phẳng (Q): 3x + 7y + 10z + 1 = 0
Lập phương trình mặt phẳng (P) đi qua ba điểm A(1;1;1), B(0;4;0), C(2;2;0)
Lập phương trình mặt phẳng theo đoạn chắn của mặt phẳng (P), biết (P) đi qua ba điểm A(5;0;0), B(0;3;0), C(0;0;6).
Viết phương trình tổng quát của mặt phẳng (P) trong mỗi trường hợp sau:
a) (P) đi qua điểm M(-3; 1; 4) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {2; - 4;1} \right)\);
b) (P) đi qua điểm N(2; -1; 5) và có cặp vectơ chỉ phương là \(\overrightarrow {{u_1}} = \left( {1; - 3; - 2} \right)\) và \(\overrightarrow {{u_2}} = \left( { - 3;4;1} \right)\);
c) (P) đi qua điểm I(4; 0; -7) và song song với mặt phẳng \(\left( Q \right):2x + y - z - 3 = 0\);
d) (P) đi qua điểm K(-4; 9; 2) và vuông góc với đường thẳng \(\Delta :\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z - 6}}{5}\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A,B,C} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x,y,z} \right)\) là một điểm tuỳ ý trong không gian.
a) Tìm toạ độ của \(\overrightarrow {{M_0}M} \).
b) Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).
c) Lập phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {0,2,1} \right)\) và có cặp vectơ chỉ phương là \(\vec a = \left( {1;3;1} \right)\), \(\vec b = \left( {2;0;1} \right)\)
a) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
b) Lập phương trình của mặt phẳng \(\left( \alpha \right)\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\).
a) Tìm toạ độ một cặp vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\).
b) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
c) Lập phương trình của mặt phẳng \(\left( \alpha \right)\).
Viết phương trình mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\).
b) \(\left( P \right)\) đi qua điểm \(B\left( { - 2;3;0} \right)\) và có cặp vectơ chỉ phương là \(\vec u = \left( {2;2; - 1} \right)\), \(\vec v = \left( {3;1;0} \right)\).
c) \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\).
d) \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\).
Viết phương trình của mặt phẳng:
a) Đi qua điểm \(A\left( {2;0;0} \right)\) và nhận \(\vec n = \left( {2;1; - 1} \right)\) làm vectơ pháp tuyến.
b) Đi qua điểm \(B\left( {1;2;3} \right)\) và song song với giá của mỗi vectơ \(\vec u = \left( {1;2;3} \right)\) và \(\vec v = \left( { - 2;0;1} \right)\).
c) Đi qua ba điểm \(A\left( {1;0;0} \right)\), \(B\left( {0;2;0} \right)\) và \(C\left( {0;0;4} \right)\).
a) Lập phương trình của các mặt phẳng toạ độ \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\).
b) Lập phương trình của các mặt phẳng đi qua điểm \(A\left( { - 1;9;8} \right)\) và lần lượt song song với các mặt phẳng toạ độ trên.
Cho tứ diện \(ABCD\) có các đỉnh \(A\left( {4;0;2} \right)\), \(B\left( {0;5;1} \right)\), \(C\left( {4; - 1;3} \right)\), \(D\left( {3; - 1;5} \right)\).
a) Hãy viết phương trình của các mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\).
b) Hãy viết phương trình mặt phẳng \(\left( P \right)\) đi qua cạnh \(BC\) và song song với cạnh \(AD\).
Viết phương trình mặt phẳng \(\left( Q \right)\) đi qua điểm \(C\left( {1; - 5;0} \right)\) và song song với mặt phẳng \(\left( P \right):3x - 5y + 4z - 2024 = 0.\)
Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua hai điểm \(A\left( {1;0;1} \right)\), \(B\left( {5;2;3} \right)\) và vuông góc với mặt phẳng \(\left( \beta \right):2x - y + z - 7 = 0\).












