Nội dung từ Loigiaihay.Com
Tính giá trị biểu thức:
\(A = \frac{2}{{4.9}} + \frac{2}{{9.14}} + \frac{2}{{14.19}} + ... + \frac{2}{{44.49}}\)
Sử dụng kiến thức \(\frac{{b - a}}{{a.b}} = \frac{1}{a} - \frac{1}{b}\) để tính A.
\(\begin{array}{l}A = \frac{2}{{4.9}} + \frac{2}{{9.14}} + \frac{2}{{14.19}} + ... + \frac{2}{{44.49}}\\ = \frac{2}{5}\left( {\frac{5}{{4.9}} + \frac{5}{{9.14}} + \frac{5}{{14.19}} + ... + \frac{5}{{44.49}}} \right)\end{array}\)
= \(\frac{2}{5}.\left( {\frac{1}{4} - \frac{1}{9} + \frac{1}{9} - \frac{1}{{14}} + \frac{1}{{14}} - \frac{1}{{19}} + ... + \frac{1}{{44}} - \frac{1}{{49}}} \right)\)
= \(\frac{2}{5}.\left( {\frac{1}{4} - \frac{1}{{49}}} \right) = \frac{2}{5}.\frac{{45}}{{196}} = \frac{9}{{98}}\)

Các bài tập cùng chuyên đề
Trong hình vẽ dưới đây có bao nhiêu bộ ba điểm thẳng hàng?
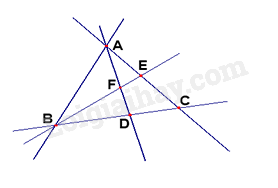
Cho hình vẽ dưới đây. Có bao nhiêu cặp đường thẳng song song?
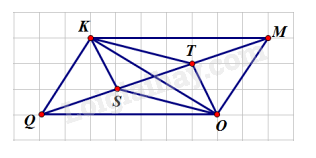
1) Cho điểm A nằm giữa hai điểm O và B sao cho \(OA{\rm{ }} = {\rm{ }}3{\rm{cm}};{\rm{ }}OB{\rm{ }} = {\rm{ }}6{\rm{cm}}.\)
a) Tính độ dài đoạn thẳng\(AB\)?
b) Điểm \(A\) có là trung điểm của đoạn thẳng \(OB\) không? Vì sao?
2) Kể tên các góc có trong hình sau












